Dada una array arr de tamaño N y Q consultas de la forma [L, R] , la tarea es encontrar el número de divisores del producto de esta array en el rango dado.
Prerrequisito: Algoritmo de MO , Inverso multiplicativo modular , Factorización prima usando tamiz
Ejemplos:
Entrada: arr[] = {4, 1, 9, 12, 5, 3}, Q = {{1, 3}, {3, 5}}
Salida:
9
24
Entrada: arr[] = {5, 2, 3, 1, 4}, Q = {{2, 4}, {1, 5}}
Salida:
4
16
Enfoque:
la idea del algoritmo de MO es preprocesar todas las consultas para que el resultado de una consulta se pueda usar en la siguiente consulta.
Sea a[0…n-1] una array de entrada y q[0..m-1] una array de consultas.
- Ordene todas las consultas de manera que las consultas con valores L de 0 a √n – 1 se junten, luego todas las consultas de √n a 2×√n – 1 , y así sucesivamente. Todas las consultas dentro de un bloque se clasifican en orden creciente de valores R.
- Procese todas las consultas una por una de manera que cada consulta use el resultado calculado en la consulta anterior. Deje que ‘resultado’ sea el resultado de una consulta anterior
- Un número n se puede representar como n =
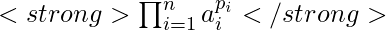, donde a i son factores primos y p i son potencias integrales de ellos.
Entonces, para esta factorización tenemos una fórmula para encontrar el número total de divisores de n y eso es:
- En la función Agregar , incrementamos la array de contadores como, por ejemplo, contador[a[i]]=contador[a[i]]+ p i . Let ‘prev’ almacena el valor anterior de contador[a[i]]. Ahora, a medida que cambia la array de contadores, el resultado cambia como:
- resultado = resultado / (prev + 1) (Dividir por prev+1 neutraliza el efecto de p i anterior )
- resultado = (resultado × (contador[p i ] + 1) (Ahora el resultado anterior se neutraliza, así que multiplicamos con el nuevo conteo, es decir, contador[a[i]]+1)
- En la función Eliminar , decrementamos la array de contadores como counter[a[i]] = counter[a[i]] – p i . Ahora, a medida que cambia la array de contadores, el resultado cambia como:
- resultado = resultado / (prev + 1) (Dividir por prev+1 neutraliza el efecto de p i anterior )
- resultado = (resultado × (contador[p i ] + 1) (Ahora el resultado anterior se neutraliza, así que
multiplicamos con el nuevo conteo, es decir, contador[a[i]]+1)
A continuación se muestra la implementación del enfoque anterior.
CPP
// C++ program to Count the divisors
// of product of an Array in range
// L to R for Q queries
#include <bits/stdc++.h>
using namespace std;
#define MAX 1000000
#define MOD 1000000007
#define ll long long int
// Variable to represent block size.
// This is made global so compare()
// of sort can use it.
int block;
// Structure to represent a query range
struct Query {
int L, R;
};
// Store the prime factor of numbers
// till MAX
vector<pair<int, int> > store[MAX + 1];
// Initialized to store the count
// of prime factors
int counter[MAX + 1] = {};
// Result is Initialized to 1
int result = 1;
// Inverse array to store
// inverse of number from 1 to MAX
ll inverse[MAX + 1];
// Function used to sort all queries so that
// all queries of the same block are arranged
// together and within a block, queries are
// sorted in increasing order of R values.
bool compare(Query x, Query y)
{
// Different blocks, sort by block.
if (x.L / block != y.L / block)
return x.L / block < y.L / block;
// Same block, sort by R value
return x.R < y.R;
}
// Function to calculate modular
// inverse and storing it in Inverse array
void modularInverse()
{
inverse[0] = inverse[1] = 1;
for (int i = 2; i <= MAX; i++)
inverse[i] = inverse[MOD % i]
* (MOD - MOD / i)
% MOD;
}
// Function to use Sieve to compute
// and store prime numbers
void sieve()
{
store[1].push_back({ 1, 0 });
for (int i = 2; i <= MAX; i++)
{
if (store[i].size() == 0)
{
store[i].push_back({ i, 1 });
for (int j = 2 * i; j <= MAX; j += i)
{
int cnt = 0;
int x = j;
while (x % i == 0)
cnt++, x /= i;
store[j].push_back({ i, cnt });
}
}
}
}
// Function to Add elements
// of current range
void add(int currL, int a[])
{
int value = a[currL];
for (auto it = store[value].begin();
it != store[value].end(); it++) {
// it->first is ai
// it->second is its integral power
int prev = counter[it->first];
counter[it->first] += it->second;
result = (result * inverse[prev + 1])
% MOD;
result = (result *
(counter[it->first] + 1))
% MOD;
}
}
// Function to remove elements
// of previous range
void remove(int currR, int a[])
{
int value = a[currR];
for (auto it = store[value].begin();
it != store[value].end(); it++) {
// it->first is ai
// it->second is its integral power
int prev = counter[it->first];
counter[it->first] -= it->second;
result = (result * inverse[prev + 1])
% MOD;
result = (result *
(counter[it->first] + 1))
% MOD;
}
}
// Function to print the answer.
void queryResults(int a[], int n, Query q[],
int m)
{
// Find block size
block = (int)sqrt(n);
// Sort all queries so that queries of
// same blocks are arranged together.
sort(q, q + m, compare);
// Initialize current L, current R and
// current result
int currL = 0, currR = 0;
for (int i = 0; i < m; i++) {
// L and R values of current range
int L = q[i].L, R = q[i].R;
// Add Elements of current range
while (currR <= R) {
add(currR, a);
currR++;
}
while (currL > L) {
add(currL - 1, a);
currL--;
}
// Remove element of previous range
while (currR > R + 1)
{
remove(currR - 1, a);
currR--;
}
while (currL < L) {
remove(currL, a);
currL++;
}
cout << result << endl;
}
}
// Driver Code
int main()
{
// Precomputing the prime numbers
// using sieve
sieve();
// Precomputing modular inverse of
// numbers from 1 to MAX
modularInverse();
int a[] = { 5, 2, 3, 1, 4 };
int n = sizeof(a) / sizeof(a[0]);
Query q[] = { { 1, 3 }, { 0, 4 } };
int m = sizeof(q) / sizeof(q[0]);
// Answer the queries
queryResults(a, n, q, m);
return 0;
}
Producción:
4 16
Complejidad del tiempo: O(Q×sqrt(N))
Publicación traducida automáticamente
Artículo escrito por saurabhshadow y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA