Cuente cuadrados de dimensiones únicas posibles a partir de líneas rectas dadas paralelas a los ejes

Dados dos arreglos X[] e Y[] que consisten en N y M enteros tales que hay N líneas paralelas al eje y y M líneas paralelas al eje x , la tarea es encontrar el número total de cuadrados que tienen un único dimensiones que se pueden generar a partir de las líneas rectas dadas .

Cada número entero (por ejemplo , a ) en la array X[] denota líneas que tienen la ecuación x = a , paralelas al 
eje y . 
Cada número entero (digamos b ) en la array Y[] denota líneas que tienen la ecuación y = b , paralelas al 
eje x . 

Ejemplos:

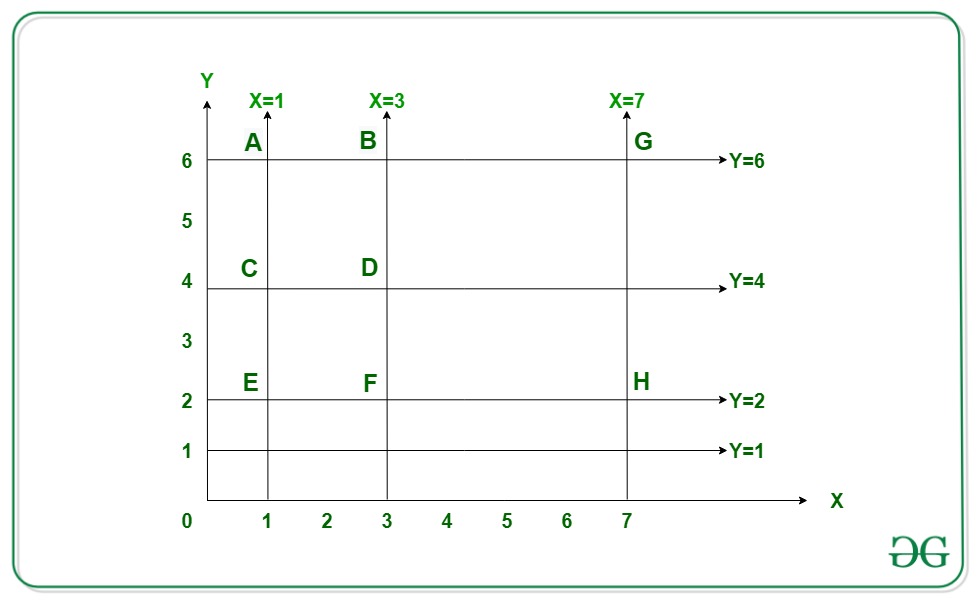
Entrada: X[] = {1, 3, 7}, Y[] = {1, 2, 4, 6}
Salida: 2 
Explicación:

De la figura anterior, hay dos posibles cuadrados de dimensiones únicas que son posibles:
ABDC
BGHF

Entrada: X[] = {2, 6, 7, 8}, Y[] = {1, 3, 5, 7}
Salida: 3

Enfoque ingenuo: el enfoque más simple es verificar cada dimensión vertical posible si existe una dimensión horizontal igual. La complejidad temporal de este enfoque se puede reducir con la ayuda del mapa . Mediante el uso de un mapa, podemos obtener todas las diferentes dimensiones verticales/horizontales.
i> Complejidad Temporal: O((N ² )*log N)
Espacio Auxiliar: O(N)

Enfoque eficiente: para optimizar el enfoque anterior, la idea es generar todas las dimensiones posibles con la ayuda de conjuntos de bits . Siga los pasos a continuación para resolver este problema:

• Inicialice conjuntos de bits para líneas horizontales y verticales de la array X[] e Y[] respectivamente.
• Establecer posiciones de líneas verticales y horizontales en el conjunto de bits.
• Mantenga otro conjunto de bits hdiff y vdiff que almacene las diferentes dimensiones posibles de los cuadrados. Las dimensiones se pueden obtener cambiando los bits establecidos en el conjunto de bits original.
• Después de los pasos anteriores, el recuento único de cuadrados es el recuento del elemento común en hdiff y vdiff que se calcula mediante (hdiff&vdiff).count() .

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
  
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
  
// Function to find the number of
// unique squares
int countSquares(int* hor, int* ver,
                 int n, int m)
{
    // Positions of the X[] and Y[]
    // are set in the bitsets hpos
    // and vpos respectively
    bitset<N> hpos, vpos;
  
    for (int i = 0; i < n; ++i) {
        hpos.set(hor[i]);
    }
    for (int i = 0; i < m; ++i) {
        vpos.set(ver[i]);
    }
  
    // Stores all possible sides of the
    // square are set in the bitsets
    // having difference hdiff & vdiff
    bitset<N> hdiff, vdiff;
  
    for (int i = 0; i < n; ++i) {
        hdiff = hdiff | (hpos >> hor[i]);
    }
    for (int i = 0; i < m; ++i) {
        vdiff = vdiff | (vpos >> ver[i]);
    }
  
    // Finding the number of square
    // sides which are common to both
    int common = (hdiff & vdiff).count();
  
    // Print the count of squares
    cout << common - 1;
}
  
// Driver Code
int main()
{
    // Given horizontal line segments
    int X[] = { 1, 3, 7 };
  
    // Given vertical line segments
    int Y[] = { 1, 2, 4, 6 };
  
    int N = (sizeof(X) / sizeof(X[0]));
    int M = (sizeof(Y) / sizeof(Y[0]));
  
    // Function Call
    countSquares(X, Y, N, M);
  
    return 0;
}

2

Complejidad temporal: O(N + M)
Espacio auxiliar: O(maxE), donde maxE es el elemento máximo entre las arrays X[] e Y[].