Contar cuadrados de tamaño K inscritos en un cuadrado de tamaño N

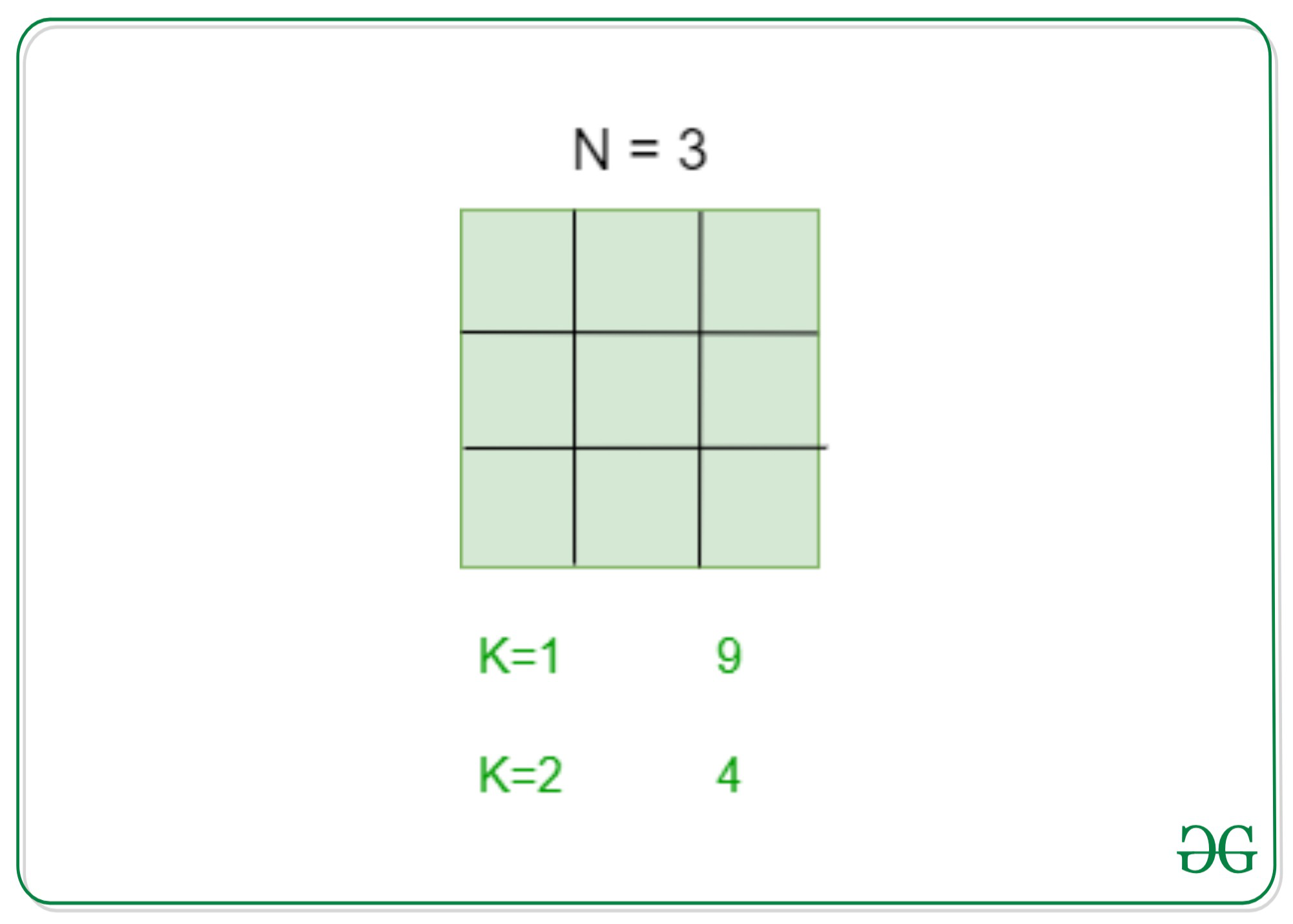
Dados dos números enteros N y K , la tarea es encontrar el número de cuadrados de tamaño K que están inscritos en un cuadrado de tamaño N .

Ejemplos:

Entrada: N = 4, K = 2
Salida: 9
Explicación:
Hay 9 cuadrados de tamaño 2 inscritos en un cuadrado de tamaño 4.

Entrada: N = 5, K = 3
Salida: 9
Explicación:
Hay 9 cuadrados de tamaño 3 inscritos en un cuadrado de tamaño 5.

Enfoque: La observación clave para resolver el problema es que el número total de cuadrados en un cuadrado de tamaño N es (N * (N + 1)* (2*N + 1)) / 6 . Por lo tanto, el número total de cuadrados de tamaño K posibles a partir de un cuadrado de tamaño N son:

A continuación se muestra la implementación del enfoque anterior:

// C++ implementation of the
// above approach
 
#include <iostream>
using namespace std;
 
// Function to calculate the number
// of squares of size K in a square
// of size N
int No_of_squares(int N, int K)
{
    // Stores the number of squares
    int no_of_squares = 0;
 
    no_of_squares
        = (N - K + 1) * (N - K + 1);
 
    return no_of_squares;
}
 
// Driver Code
int main()
{
    // Size of the
    // bigger square
    int N = 5;
 
    // Size of
    // smaller square
    int K = 3;
    cout << No_of_squares(N, K);
    return 0;
}

// Java implementation of the
// above approach
import java.util.*;
class GFG{
 
// Function to calculate the
// number of squares of size
// K in a square of size N
static int No_of_squares(int N,
                         int K)
{
  // Stores the number
  // of squares
  int no_of_squares = 0;
 
  no_of_squares = (N - K + 1) *
                  (N - K + 1);
 
  return no_of_squares;
}
 
// Driver Code
public static void main(String[] args)
{
  // Size of the
  // bigger square
  int N = 5;
 
  // Size of
  // smaller square
  int K = 3;
  System.out.print(No_of_squares(N, K));
}
}
 
// This code is contributed by Princi Singh

# Python3 implementation of the
# above approach
 
# Function to calculate the
# number of squares of size
# K in a square of size N
def No_of_squares(N, K):
   
    # Stores the number
    # of squares
    no_of_squares = 0;
    no_of_squares = (N - K + 1) * (N - K + 1);
    return no_of_squares;
 
# Driver Code
if __name__ == '__main__':
   
    # Size of the
    # bigger square
    N = 5;
 
    # Size of
    # smaller square
    K = 3;
    print(No_of_squares(N, K));
 
# This code is contributed by 29AjayKumar

// C# implementation of the
// above approach
using System;
 
class GFG{
 
// Function to calculate the
// number of squares of size
// K in a square of size N
static int No_of_squares(int N, int K)
{
     
    // Stores the number
    // of squares
    int no_of_squares = 0;
     
    no_of_squares = (N - K + 1) *
                    (N - K + 1);
     
    return no_of_squares;
}
 
// Driver Code
public static void Main(String[] args)
{
     
    // Size of the
    // bigger square
    int N = 5;
     
    // Size of
    // smaller square
    int K = 3;
     
    Console.Write(No_of_squares(N, K));
}
}
 
// This code is contributed by Amit Katiyar

<script>
 
// JavaScript program for
// the above approach
 
// Function to calculate the
// number of squares of size
// K in a square of size N
function No_of_squares(N, K)
{
  // Stores the number
  // of squares
  let no_of_squares = 0;
  
  no_of_squares = (N - K + 1) *
                  (N - K + 1);
  
  return no_of_squares;
}
 
// Driver code
 
    // Size of the
  // bigger square
  let N = 5;
  
  // Size of
  // smaller square
  let K = 3;
  document.write(No_of_squares(N, K));
   
  // This code is contributed by splevel62.
</script>

9

Tiempo Complejidad: O(1) 
Espacio Auxiliar: O(1)