Cuente el número de ceros finales en (1^1)*(2^2)*(3^3)*(4^4)*..

Posted on by Rudeus Greyrat

Dado un número entero n , la tarea es encontrar el número de ceros finales en la función, 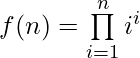 f(n)=\prod\limits_{i = 1}^{n} i^{i} es decir , f(n) = 1 1 * 2 2 * 3 3 * … * n n .

Ejemplos: 

Entrada: n = 5 
Salida: 5 
f(5) = 1 1 * 2 2 * 3 3 * 4 4 * 5 5 = 1 * 4 * 27 * 256 * 3125 = 86400000

Entrada: n = 12 
Salida: 15 
 

Enfoque: sabemos que 5 * 2 = 10 , es decir, 1 cero final es el resultado de la multiplicación de un solo 5 y un solo 2. Entonces, si tenemos x número de 5 e y número de 2 , entonces el número de ceros finales será sea ​​min(x, y) . 
Ahora, para cada número i en la serie, necesitamos contar el número de 2 y 5 en sus factores, digamos x e y , pero el número de 2 y 5 será x * i e y * i respectivamente porque en la serie ise eleva a la potencia misma, es decir i i . Cuente el número de 2 y 5 en la serie completa e imprima el mínimo de ellos, que es la respuesta requerida.

A continuación se muestra la implementación del enfoque anterior:  

C++

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to return the number of
// trailing zeros
int trailing_zeros(int N)
{
 
    // To store the number of 2s and 5s
    int count_of_two = 0, count_of_five = 0;
 
    for (int i = 1; i <= N; i++) {
 
        int val = i;
 
        while (val % 2 == 0 && val > 0) {
            val /= 2;
 
            // If we get a factor 2 then we
            // have i number of 2s because
            // the power of the number is
            // raised to i
            count_of_two += i;
        }
 
        while (val % 5 == 0 && val > 0) {
            val /= 5;
 
            // If we get a factor 5 then
            // we have i number of 5s
            // because the power of the
            // number is raised to i
            count_of_five += i;
        }
    }
 
    // Take the minimum of them
    int ans = min(count_of_two, count_of_five);
 
    return ans;
}
 
// Driver code
int main()
{
    int N = 12;
 
    cout << trailing_zeros(N);
 
    return 0;
}

Java

// Java implementation of the approach
 
class GFG
{
     
// Function to return the number of
// trailing zeros
static int trailing_zeros(int N)
{
 
    // To store the number of 2s and 5s
    int count_of_two = 0, count_of_five = 0;
 
    for (int i = 1; i <= N; i++)
    {
        int val = i;
        while (val % 2 == 0 && val > 0)
        {
            val /= 2;
 
            // If we get a factor 2 then we
            // have i number of 2s because
            // the power of the number is
            // raised to i
            count_of_two += i;
        }
 
        while (val % 5 == 0 && val > 0)
        {
            val /= 5;
 
            // If we get a factor 5 then
            // we have i number of 5s
            // because the power of the
            // number is raised to i
            count_of_five += i;
        }
    }
 
    // Take the minimum of them
    int ans = Math.min(count_of_two, count_of_five);
 
    return ans;
}
 
// Driver code
public static void main (String[] args)
{
    int N = 12;
    System.out.println(trailing_zeros(N));
}
}
 
// This code is contributed by chandan_jnu

Python3

# Python 3 implementation of the approach
 
# Function to return the number of
# trailing zeros
def trailing_zeros(N):
     
    # To store the number of 2s and 5s
    count_of_two = 0
    count_of_five = 0
 
    for i in range(1, N + 1, 1):
        val = i
 
        while (val % 2 == 0 and val > 0):
            val /= 2
 
            # If we get a factor 2 then we
            # have i number of 2s because
            # the power of the number is
            # raised to i
            count_of_two += i
 
        while (val % 5 == 0 and val > 0):
            val /= 5
 
            # If we get a factor 5 then we
            # have i number of 5s because
            # the power of the number is
            # raised to i
            count_of_five += i
     
    # Take the minimum of them
    ans = min(count_of_two, count_of_five)
 
    return ans
 
# Driver code
if __name__ == '__main__':
    N = 12
 
    print(trailing_zeros(N))
 
# This code is contributed by
# Sanjit_Prasad

C#

// C# implementation of the above approach
using System;
 
class GFG
{
     
    // Function to return the number of
    // trailing zeros
    static int trailing_zeros(int N)
    {
     
        // To store the number of 2s and 5s
        int count_of_two = 0, count_of_five = 0;
     
        for (int i = 1; i <= N; i++)
        {
            int val = i;
            while (val % 2 == 0 && val > 0)
            {
                val /= 2;
     
                // If we get a factor 2 then we
                // have i number of 2s because
                // the power of the number is
                // raised to i
                count_of_two += i;
            }
     
            while (val % 5 == 0 && val > 0)
            {
                val /= 5;
     
                // If we get a factor 5 then
                // we have i number of 5s
                // because the power of the
                // number is raised to i
                count_of_five += i;
            }
        }
     
        // Take the minimum of them
        int ans = Math.Min(count_of_two, count_of_five);
     
        return ans;
    }
     
    // Driver code
    public static void Main()
    {
        int N = 12;
        Console.WriteLine(trailing_zeros(N));
    }
}
 
// This code is contributed by Ryuga

PHP

<?php
// PHP implementation of the approach
 
// Function to return the number of
// trailing zeros
function trailing_zeros($N)
{
 
    // To store the number of 2s and 5s
    $count_of_two = 0;
    $count_of_five = 0;
 
    for ($i = 1; $i <= $N; $i++)
    {
        $val = $i;
 
        while ($val % 2 == 0 && $val > 0)
        {
            $val /= 2;
 
            // If we get a factor 2 then we
            // have i number of 2s because
            // the power of the number is
            // raised to i
            $count_of_two += $i;
        }
 
        while ($val % 5 == 0 && $val > 0)
        {
            $val /= 5;
 
            // If we get a factor 5 then
            // we have i number of 5s
            // because the power of the
            // number is raised to i
            $count_of_five += $i;
        }
    }
 
    // Take the minimum of them
    $ans = min($count_of_two, $count_of_five);
 
    return $ans;
}
 
// Driver code
$N = 12;
echo trailing_zeros($N);
 
// This code is contributed by ita_c
?>

Javascript

<script>
 
// Javascript implementation of the approach
 
// Function to return the number of
// trailing zeros
function trailing_zeros(N)
{
     
    // To store the number of 2s and 5s
    let count_of_two = 0, count_of_five = 0;
 
    for(let i = 1; i <= N; i++)
    {
        let val = i;
 
        while (val % 2 == 0 && val > 0)
        {
            val = parseInt(val / 2);
 
            // If we get a factor 2 then we
            // have i number of 2s because
            // the power of the number is
            // raised to i
            count_of_two += i;
        }
 
        while (val % 5 == 0 && val > 0)
        {
            val = parseInt(val / 5);
 
            // If we get a factor 5 then
            // we have i number of 5s
            // because the power of the
            // number is raised to i
            count_of_five += i;
        }
    }
 
    // Take the minimum of them
    let ans = Math.min(count_of_two,
                       count_of_five);
 
    return ans;
}
 
// Driver code
let N = 12;
 
document.write(trailing_zeros(N));
 
// This code is contributed by subhammahato348
 
</script>
Producción: 

15

 

Complejidad de tiempo: O(N * (log 2 N + log 5 N))

Espacio Auxiliar: O(1), ya que no se ha ocupado ningún espacio extra.

Publicación traducida automáticamente

Artículo escrito por souradeep y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *