Cuente las posibles decodificaciones de una secuencia de dígitos determinada | conjunto 2

Dada una string codificada str que consta de dígitos y * que se puede completar con cualquier dígito del 1 al 9 , la tarea es encontrar el número de formas de decodificar esa string en una secuencia de alfabetos AZ .

Nota: La string de entrada contiene números del 0 al 9 y el carácter ‘*’ únicamente. 

Ejemplos: 

Entrada: str = “1*” 
Salida: 18 
Explicación: 
Dado que * se puede reemplazar por cualquier valor de (1-9), 
la string dada se puede decodificar como A[AI] + [JR] = 9 + 9 formas

Entrada: str = “12*3” 
Salida: 28 
 

Enfoque ingenuo: una solución simple es resolver el problema usando la recursividad considerando todas las posibles decodificaciones de la string.

 A continuación se muestra el árbol de recursión para el problema:

                   12*3
              /             \
           12*(3)           12(*3) 
         /     \            /      \
    12(*)(3)  1(2*)(3)  1(2)(*3)   ""
      /    \      \       /
1(2)(*)(3) ""     ""     ""   
    /
   ""

Enfoque Eficiente: La idea es resolver el problema utilizando Programación Dinámica utilizando la subestructura óptima para considerar todos los casos de los dígitos actuales y anteriores de la string y su número de formas de decodificar la string. 

Definición del estado DP: en este problema,  denota el número de formas de decodificar la string hasta el  índice.

Estados iniciales de DP: Inicialmente, el valor de los estados de DP se define a continuación: 

// Number of ways to decode 
// an empty string
dp[0] = 1

// Number of ways to decode the
// first character
if (s[0] == '*')
    dp[1] = 9  // 9 ways
else 
    dp[1] = 1

Subestructura óptima: generalmente hay dos formas de decodificar el carácter actual de la string:

• Incluir el carácter actual como un solo dígito para decodificar: si el carácter actual se usa como un solo dígito, generalmente puede haber dos casos para que el carácter sea: 
  • Caso 1: si el carácter actual es igual a  , entonces hay 9 formas posibles de tomar cualquier dígito de [1-9] y decodificarlo como cualquier carácter de [AZ].

if (current == "*")
    dp[i] += 9 * dp[i-1]

• Caso 2: si el carácter actual es igual a cualquier otro dígito de [0-9], entonces el número de formas posibles de decodificar es igual al número de formas de decodificar la string hasta el 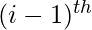 índice.

if (current != "*")
     dp[i] += dp[i-1]

• Incluir el carácter actual como dos dígitos para decodificar: si el carácter actual se va a decodificar como dos dígitos, hay dos casos posibles: 
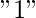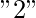  • Caso 1: si el carácter anterior es igual a  o  , entonces puede haber dos subcasos más posibles que dependerán del carácter actual: 
    • Caso 1.1: si el carácter actual es igual a  , entonces el total de formas posibles de decodificar es 9 si el carácter anterior es 1, de lo contrario, 6 si el carácter anterior es 2.
    • Caso 1.2: si el carácter actual es menor que igual a 6, entonces el número total de formas posibles de decodificar la string dependerá solo del número de formas de decodificar hasta el carácter anterior. Eso es 
  • Caso 2: si el carácter anterior es  , entonces puede haber dos subcasos más posibles que dependerán del carácter actual: 
    • Caso 2.1: si el carácter actual también es  , entonces el número total de casos será  , porque los dígitos individuales de las formas de decodificación del carácter anterior ya deben estar incluidos.
    • Caso 2.2: Si el carácter actual es menor que 6, entonces el número total de formas será  , porque entonces el número de formas para elegir los dígitos del primer carácter es 2. Eso es [1, 2].
    • Caso 2.3: si el carácter actual es cualquier dígito, entonces el número total de formas será el número de formas de decodificar hasta el dígito anterior solamente. eso  es

// C++ implementation to count the
// possible decodings of the given
// digit sequence
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to count the number of
// ways to decode the given digit
// sequence
int waysToDecode2(string s) {
    int n = s.size();
     
    // Array to store the dp states
    vector<int> dp(n+1,0);
     
    // Case of empty string
    dp[0]=1;
     
    // Condition to check if the
    // first character of string is 0
    if(s[0]=='0')
        return 0;
         
    // Base case for single length
    // string
    dp[1]= ((s[0]=='*')? 9 : 1);
     
    // Bottom-up dp for the string
    for(int i=2;i<=n;i++)
    {
        // Previous character
        char first= s[i-2];
         
        // Current character
        char second= s[i-1];
         
        // Case to include the Current
        // digit as a single digit for
        // decoding the string
        if(second=='*')
        {
            dp[i]+= 9*dp[i-1];
        }
        else if(second>'0')
            dp[i]+=dp[i-1];
         
        // Case to include the current
        // character as two-digit for
        // decoding the string
        if(first=='1'|| first=='2')
        {
             
            // Condition to check if the
            // current character is "*"
            if(second=='*')
            {
                if(first=='1')
                    dp[i]+= 9 * dp[i-2];
                else if(first=='2')
                    dp[i]+= 6 * dp[i-2];
            }
             
            // Condition to check if the
            // current character is less than
            // or equal to 26
            else if(((first-'0')* 10 +
                    (second-'0'))<= 26)
                dp[i]+=dp[i-2];
        }
         
        // Condition to check if the
        // Previous digit is equal to "*"
        else if(first=='*')
        {
            if(second=='*')
            {
                dp[i]+= 15 * dp[i-2];
            }
            else if(second<='6')
                dp[i]+= 2* dp[i-2];
            else
                dp [i]+= dp[i-2];
        }
    }
    return dp[n];
}
 
// Driver Code
int main() {
    string str = "12*3";
     
    // Function Call
    cout << waysToDecode2(str) << endl;
    return 0;
}

// Java implementation to count the
// possible decodings of the given
// digit sequence
class GFG{
 
// Function to count the number of
// ways to decode the given digit
// sequence
static int waysToDecode2(char []s)
{
     
    int n = s.length;
     
    // Array to store the dp states
    int []dp = new int[n + 1];
     
    // Case of empty String
    dp[0] = 1;
     
    // Condition to check if the
    // first character of String is 0
    if(s[0] == '0')
        return 0;
         
    // Base case for single length
    // String
    dp[1] = ((s[0] == '*') ? 9 : 1);
     
    // Bottom-up dp for the String
    for(int i = 2; i <= n; i++)
    {
         
    // Previous character
    char first = s[i - 2];
         
    // Current character
    char second = s[i - 1];
         
    // Case to include the Current
    // digit as a single digit for
    // decoding the String
    if(second == '*')
    {
        dp[i] += 9 * dp[i - 1];
    }
    else if(second > '0')
        dp[i] += dp[i - 1];
         
    // Case to include the current
    // character as two-digit for
    // decoding the String
    if(first == '1' || first == '2')
    {
             
        // Condition to check if the
        // current character is "*"
        if(second == '*')
        {
            if(first == '1')
                dp[i] += 9 * dp[i - 2];
            else if(first == '2')
                dp[i] += 6 * dp[i - 2];
        }
             
        // Condition to check if the
        // current character is less than
        // or equal to 26
        else if(((first - '0') * 10 +
                (second - '0')) <= 26)
        {
            dp[i] += dp[i - 2];
        }
    }
         
    // Condition to check if the
    // previous digit is equal to "*"
    else if(first == '*')
    {
        if(second == '*')
        {
            dp[i] += 15 * dp[i - 2];
        }
        else if(second <= '6')
        {
            dp[i] += 2 * dp[i - 2];
        }
        else
        {
            dp[i] += dp[i - 2];
        }
    }
    }
    return dp[n];
}
 
// Driver Code
public static void main(String[] args)
{
    String str = "12*3";
     
    // Function Call
    System.out.print(waysToDecode2(
                    str.toCharArray()) + "\n");
}
}
 
// This code is contributed by amal kumar choubey

// C# implementation to count the
// possible decodings of the given
// digit sequence
using System;
 
class GFG{
 
// Function to count the number of
// ways to decode the given digit
// sequence
static int waysToDecode2(char []s)
{
    int n = s.Length;
     
    // Array to store the dp states
    int []dp = new int[n + 1];
     
    // Case of empty String
    dp[0] = 1;
     
    // Condition to check if the
    // first character of String is 0
    if(s[0] == '0')
        return 0;
         
    // Base case for single length
    // String
    dp[1] = ((s[0] == '*') ? 9 : 1);
     
    // Bottom-up dp for the String
    for(int i = 2; i <= n; i++)
    {
         
    // Previous character
    char first = s[i - 2];
         
    // Current character
    char second = s[i - 1];
         
    // Case to include the current
    // digit as a single digit for
    // decoding the String
    if(second == '*')
    {
        dp[i] += 9 * dp[i - 1];
    }
    else if(second > '0')
    {
        dp[i] += dp[i - 1];
    }
         
    // Case to include the current
    // character as two-digit for
    // decoding the String
    if(first == '1' || first == '2')
    {
             
        // Condition to check if the
        // current character is "*"
        if(second == '*')
        {
            if(first == '1')
            {
                dp[i] += 9 * dp[i - 2];
            }
            else if(first == '2')
            {
                dp[i] += 6 * dp[i - 2];
            }
        }
             
        // Condition to check if the
        // current character is less than
        // or equal to 26
        else if(((first - '0') * 10 +
                (second - '0')) <= 26)
        {
            dp[i] += dp[i - 2];
        }
    }
         
    // Condition to check if the
    // previous digit is equal to "*"
    else if(first == '*')
    {
        if(second == '*')
        {
            dp[i] += 15 * dp[i - 2];
        }
        else if(second <= '6')
        {
            dp[i] += 2 * dp[i - 2];
        }
        else
        {
            dp[i] += dp[i - 2];
        }
    }
    }
    return dp[n];
}
 
// Driver Code
public static void Main(String[] args)
{
    String str = "12*3";
     
    // Function Call
    Console.Write(waysToDecode2(
                str.ToCharArray()) + "\n");
}
}
 
// This code is contributed by amal kumar choubey

<script>
 
// JavaScript implementation to count the
// possible decodings of the given
// digit sequence
 
// Function to count the number of
// ways to decode the given digit
// sequence
function waysToDecode2(s)
{
         
    let n = s.length;
         
    // Array to store the dp states
    let dp = Array.from({length: n+1}, (_, i) => 0);
         
    // Case of empty String
    dp[0] = 1;
         
    // Condition to check if the
    // first character of String is 0
    if(s[0] == '0')
        return 0;
             
    // Base case for single length
    // String
    dp[1] = ((s[0] == '*') ? 9 : 1);
         
    // Bottom-up dp for the String
    for(let i = 2; i <= n; i++)
    {
         
    // Previous character
    let first = s[i - 2];
         
    // Current character
    let second = s[i - 1];
         
    // Case to include the Current
    // digit as a single digit for
    // decoding the String
    if(second == '*')
    {
        dp[i] += 9 * dp[i - 1];
    }
    else if(second > '0')
        dp[i] += dp[i - 1];
         
    // Case to include the current
    // character as two-digit for
    // decoding the String
    if(first == '1' || first == '2')
    {
             
        // Condition to check if the
        // current character is "*"
        if(second == '*')
        {
            if(first == '1')
                dp[i] += 9 * dp[i - 2];
            else if(first == '2')
                dp[i] += 6 * dp[i - 2];
        }
             
        // Condition to check if the
        // current character is less than
        // or equal to 26
        else if(((first - '0') * 10 +
                (second - '0')) <= 26)
        {
            dp[i] += dp[i - 2];
        }
    }
         
    // Condition to check if the
    // previous digit is equal to "*"
    else if(first == '*')
    {
        if(second == '*')
        {
            dp[i] += 15 * dp[i - 2];
        }
        else if(second <= '6')
        {
            dp[i] += 2 * dp[i - 2];
        }
        else
        {
            dp[i] += dp[i - 2];
        }
    }
    }
    return dp[n];
}
     
 
// Driver Code
 
        let str = "12*3";
         
    // Function Call
    document.write(waysToDecode2(
                    str.split('')) + "\n");
             
</script>

# Python3 implementation to count the
# possible decodings of the given
# digit sequence
 
 
# Function to count the number of
# ways to decode the given digit
# sequence
def waysToDecode2(s):
    n = len(s)
 
    # Array to store the dp states
    dp = [0] * (n + 1)
 
    # Case of empty string
    dp[0] = 1
 
    # Condition to check if the
    # first character of string is 0
    if s[0] == "0":
        return 0
 
    # Base case for single length
    # string
    dp[1] = 9 if (s[0] == "*") else 1
 
    # Bottom-up dp for the string
    for i in range(2, n+1):
        # Previous character
        first = s[i - 2]
 
        # Current character
        second = s[i - 1]
 
        # Case to include the Current
        # digit as a single digit for
        # decoding the string
        if second == "*":
            dp[i] += 9 * dp[i - 1]
 
        elif second > "0":
            dp[i] += dp[i - 1]
 
        # Case to include the current
        # character as two-digit for
        # decoding the string
        if first == "1" or first == "2":
 
            # Condition to check if the
            # current character is "*"
            if second == "*":
                if first == "1":
                    dp[i] += 9 * dp[i - 2]
                elif first == "2":
                    dp[i] += 6 * dp[i - 2]
 
            # Condition to check if the
            # current character is less than
            # or equal to 26
            elif (ord(first) - ord("0")) * 10 + (ord(second) - ord("0")) <= 26:
                dp[i] += dp[i - 2]
 
        # Condition to check if the
        # Previous digit is equal to "*"
        elif first == "*":
            if second == "*":
                dp[i] += 15 * dp[i - 2]
 
            elif second <= "6":
                dp[i] += 2 * dp[i - 2]
            else:
                dp[i] += dp[i - 2]
 
    return dp[n]
 
 
# Driver Code
if __name__ == "__main__":
    str = "12*3"
 
    # Function Call
    print(waysToDecode2(str))

Producción:

28

• Complejidad de tiempo: O(N)
• Espacio Auxiliar: O(N)