Contar puntos de una array que se encuentra dentro de un semicírculo

Dados dos pares (X, Y), (P, Q) y R , la coordenada del centro del semicírculo, la coordenada de la intersección del semicírculo y el diámetro del semicírculo y el radio del semicírculo y una array arr[ ] de dimensión N*2 que consta de las coordenadas de algunos puntos, la tarea es encontrar el número de puntos de la array que se encuentra dentro o sobre el 
semicírculo . 
Nota: Se considera el semicírculo sobre el diámetro.

Ejemplos:

Entrada: X = 0, Y = 0, R = 5, P = 5, Q = 0, arr[][] = { {2, 3}, {5, 6}, {-1, 4}, {5 , 5} }
Salida: 2
Explicación: Los puntos {2, 3} y {-1, 4} están dentro del semicírculo.

Entrada: X = 2, Y = 3, R = 10, P = 12, Q = 3, arr[][] = { {-7, -5}, {0, 6}, {11, 4} }
Salida : 2

Enfoque: El problema dado se puede resolver con base en las siguientes observaciones: 

• Los puntos que se encuentran sobre o dentro del semicírculo deben estar por encima o sobre el diámetro del semicírculo y la distancia entre el centro y ese punto debe ser ≤ R .
• Supongamos   que es la ecuación del diámetro. 
  El punto (R, S) está por encima de la recta si 
  
   
• Un punto (R, S) se encuentra por encima de la línea formada por la unión de los puntos (X, Y) y (P, Q) si

Siga los pasos a continuación para resolver el problema:

• Encuentra la ecuación de la línea del diámetro del semicírculo desde los puntos (X, Y) y (P, Q).
• Inicialice una variable, digamos ans , para almacenar el conteo de puntos requeridos.
• Recorra la array arr[] y realice las siguientes operaciones:
  • Calcula la distancia entre los puntos (X, Y) y (P, Q) y guárdala en una variable, digamos d.
  • Coloque arr[i][0] y arr[i][1] en lugar de R y S respectivamente, en la fórmula 
    
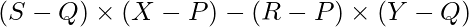
    y almacene el resultado en una variable, digamos f .
  • Incremente la cuenta de ans en 1 si R ≤ d y f ≥ 0 .
• Después de completar los pasos anteriores, imprima el valor almacenado en ans .

A continuación se muestra la implementación del enfoque anterior:

// C++ program for above approach
#include <bits/stdc++.h>
using namespace std;
 
int getPointsIns(int x1, int y1, int radius, int x2,
                 int y2, vector<pair<int, int>> points)
{
    int ans = 0;
     
    // Traverse the array
    for(int i = 0; i < points.size(); i++)
    {
         
        // Stores if a point lies
        // above the diameter or not
        bool condOne = false, condTwo = false;
        if ((points[i].second - y2) *
              (x2 - x1) - (y2 - y1) *
             (points[i].first - x2) >= 0)
        {
            condOne = true;
        }
 
        // Stores if the R is less than or
        // equal to the distance between
        // center and point
        if (radius >= (int)sqrt(pow((y1 - points[i].second), 2) +
                                 pow(x1 - points[i].first, 2)))
        {
            condTwo = true;
        }
        if (condOne && condTwo)
        {
            ans += 1;
        }
    }
    return ans;
}
 
// Driver code
int main()
{
    int X = 0;
    int Y = 0;
    int R = 5;
    int P = 5;
    int Q = 0;
 
    vector<pair<int, int>> arr = { make_pair(2, 3),
                                   make_pair(5, 6),
                                   make_pair(-1, 4),
                                   make_pair(5, 5) };
 
    cout << getPointsIns(X, Y, R, P, Q, arr);
    return 0;
}
 
// This code is contributed by nirajgusain5

// Java program for above approach
import java.io.*;
 
class Gfg {
  public static int getPointsIns(int x1, int y1,int radius,
                                 int x2,int y2, pair points[])
  {
    int ans = 0;
    // Traverse the array
    for (int i = 0; i < points.length; i++)
    {
       
      // Stores if a point lies
      // above the diameter or not
      boolean condOne = false, condTwo = false;
      if ((points[i].b - y2) *
          (x2 - x1)- (y2 - y1) *
          (points[i].a - x2)>= 0)
      {
        condOne = true;
      }
 
      // Stores if the R is less than or
      // equal to the distance between
      // center and point
      if (radius >= (int)Math.sqrt(Math.pow((y1 - points[i].b), 2)+
                                   Math.pow(x1 - points[i].a, 2)))
      {
        condTwo = true;
      }
      if (condOne && condTwo)
      {
        ans += 1;
      }
    }
    return ans;
  }
   
  // Driver code
  public static void main(String[] args)
  {
    int X = 0;
    int Y = 0;
    int R = 5;
    int P = 5;
    int Q = 0;
 
    pair arr[] = {new pair(2, 3), new pair(5, 6), new pair(-1, 4), new pair(5,5)};
 
    System.out.print(getPointsIns(X, Y, R, P, Q, arr));
  }
}
class pair
{
  int a;
  int b;
  pair(int a,int b)
  {   
    this.a = a;
    this.b = b;
  }
}

# Python implementation of above approach
def getPointsIns(x1, y1, radius, x2, y2, points):
    # Stores the count of ans
    ans = 0
 
    # Traverse the array
    for point in points:
 
        # Stores if a point lies
        # above the diameter or not
        condOne = (point[1] - y2) * (x2 - x1) \
                  - (y2 - y1) * (point[0] - x2) >= 0
 
        # Stores if the R is less than or
        # equal to the distance between
        # center and point
 
        condTwo = radius >= ((y1 - point[1]) ** 2 \
                  + (x1 - point[0]) ** 2) ** (0.5)
 
        if condOne and condTwo:
            ans += 1
 
    return ans
 
 
# Driver Code
# Input
X = 0
Y = 0
R = 5
P = 5
Q = 0
arr = [[2, 3], [5, 6], [-1, 4], [5, 5]]
 
print(getPointsIns(X, Y, R, P, Q, arr))

// C# program for above approach
using System;
 
class Gfg
{
  public static int getPointsIns(int x1, int y1,
                                 int radius, int x2,
                                 int y2, pair[] points)
  {
    int ans = 0;
     
    // Traverse the array
    for (int i = 0; i < points.Length; i++) {
 
      // Stores if a point lies
      // above the diameter or not
      bool condOne = false, condTwo = false;
      if ((points[i].b - y2) * (x2 - x1)
          - (y2 - y1) * (points[i].a - x2)
          >= 0) {
        condOne = true;
      }
 
      // Stores if the R is less than or
      // equal to the distance between
      // center and point
      if (radius >= (int)Math.Sqrt(
        Math.Pow((y1 - points[i].b), 2)
        + Math.Pow(x1 - points[i].a, 2))) {
        condTwo = true;
      }
      if (condOne && condTwo) {
        ans += 1;
      }
    }
    return ans;
  }
 
  // Driver code
  public static void Main(string[] args)
  {
    int X = 0;
    int Y = 0;
    int R = 5;
    int P = 5;
    int Q = 0;
 
    pair[] arr = { new pair(2, 3), new pair(5, 6),
                  new pair(-1, 4), new pair(5, 5) };
 
    Console.Write(getPointsIns(X, Y, R, P, Q, arr));
  }
}
public class pair {
  public int a;
  public int b;
  public pair(int a, int b)
  {
    this.a = a;
    this.b = b;
  }
}
 
// This code is contributed by code_hunt.

<script>
// Javascript program for above approach
 
function getPointsIns(x1,y1,radius,x2,y2,points)
{
    let ans = 0;
    // Traverse the array
    for (let i = 0; i < points.length; i++)
    {
        
      // Stores if a point lies
      // above the diameter or not
      let condOne = false, condTwo = false;
      if ((points[i][1] - y2) *
          (x2 - x1)- (y2 - y1) *
          (points[i][0] - x2)>= 0)
      {
        condOne = true;
      }
  
      // Stores if the R is less than or
      // equal to the distance between
      // center and point
      if (radius >= Math.sqrt(Math.pow((y1 - points[i][1]), 2)+
                                   Math.pow(x1 - points[i][0], 2)))
      {
        condTwo = true;
      }
       
      if (condOne && condTwo)
      {
        ans += 1;
      }
       
    }
    return ans;
}
 
// Driver code
let X = 0;
    let Y = 0;
    let R = 5;
    let P = 5;
    let Q = 0;
  
    let arr = [[2, 3], [5, 6], [-1, 4], [5, 5]];
  
    document.write(getPointsIns(X, Y, R, P, Q, arr));
   
 
 
 
// This code is contributed by avanitrachhadiya2155
</script>

2

Complejidad temporal: O(N)
Espacio auxiliar: O(1)