Contar subarreglos no decrecientes de tamaño N a partir de N números naturales

Dados N números naturales, la tarea es encontrar el número de subarreglos de tamaño N que se pueden formar usando elementos de 1 a N de modo que cada elemento en el subarreglo sea menor o igual que los elementos a su derecha (a[ i] ≤ a[i+1]).
Ejemplos: 
 

Entrada: N = 2 
Salida: 3 
Explicación: 
Conjunto dado de N números naturales: {1, 2} 
Subconjuntos necesarios que se pueden formar: [1, 1], [1, 2], [2, 2].
Entrada: N = 3 
Salida: 10 
Explicación: 
Conjunto dado de N números naturales: {1, 2, 3} 
Subconjuntos necesarios que se pueden formar: [1, 1, 1], [1, 1, 2], [1, 2, 2], [2, 2, 2], [1, 1, 3], [1, 3, 3], [3, 3, 3], [2, 2, 3], [2, 3, 3], [1, 2, 3]. 
 

Acercarse: 
 

• Dado que cada elemento del arreglo está entre 1 y N y los subarreglos pueden tener elementos duplicados en orden no descendente, es decir, a[0] ≤ a[1] ≤ …. ≤ un[N – 1] .
• El número de formas de elegir r objetos con reemplazo de n objetos es 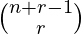 (usando Combinación con repetición ).
• Aquí r = N y n = N , ya que podemos elegir de 1 a N. Entonces, el recuento de toda la array ordenada de longitud N con elementos de 1 a N será  .
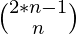• Ahora esto se puede ampliar aún más con la ayuda de los coeficientes binomiales . El coeficiente obtenido de esto será el conteo del subarreglo requerido.

A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program to count non decreasing subarrays
// of size N from N Natural numbers
 
#include <bits/stdc++.h>
using namespace std;
 
// Returns value of Binomial Coefficient C(n, k)
int binomialCoeff(int n, int k)
{
    int C[k + 1];
    memset(C, 0, sizeof(C));
 
    // Since nC0 is 1
    C[0] = 1;
 
    for (int i = 1; i <= n; i++) {
 
        // Compute next row of pascal triangle using
        // the previous row
        for (int j = min(i, k); j > 0; j--)
            C[j] = C[j] + C[j - 1];
    }
    return C[k];
}
 
// Function to find the count of required subarrays
int count_of_subarrays(int N)
{
 
    // The required count is the binomial coefficient
    // as explained in the approach above
    int count = binomialCoeff(2 * N - 1, N);
 
    return count;
}
 
// Driver Function
int main()
{
 
    int N = 3;
 
    cout << count_of_subarrays(N) << "\n";
}

// Java program to count non decreasing subarrays
// of size N from N Natural numbers
class GFG
{
 
// Returns value of Binomial Coefficient C(n, k)
static int binomialCoeff(int n, int k)
{
    int []C = new int[k + 1];
 
    // Since nC0 is 1
    C[0] = 1;
 
    for (int i = 1; i <= n; i++)
    {
 
        // Compute next row of pascal triangle using
        // the previous row
        for (int j = Math.min(i, k); j > 0; j--)
            C[j] = C[j] + C[j - 1];
    }
    return C[k];
}
 
// Function to find the count of required subarrays
static int count_of_subarrays(int N)
{
 
    // The required count is the binomial coefficient
    // as explained in the approach above
    int count = binomialCoeff(2 * N - 1, N);
 
    return count;
}
 
// Driver Function
public static void main(String[] args)
{
    int N = 3;
    System.out.print(count_of_subarrays(N)+ "\n");
}
}
 
// This code is contributed by 29AjayKumar

# Python3 program to count non decreasing subarrays
# of size N from N Natural numbers
 
# Returns value of Binomial Coefficient C(n, k)
def binomialCoeff(n, k) :
 
    C = [0] * (k + 1);
 
    # Since nC0 is 1
    C[0] = 1;
 
    for i in range(1, n + 1) :
 
        # Compute next row of pascal triangle using
        # the previous row
        for j in range(min(i, k), 0, -1) :
            C[j] = C[j] + C[j - 1];
     
    return C[k];
 
# Function to find the count of required subarrays
def count_of_subarrays(N) :
 
    # The required count is the binomial coefficient
    # as explained in the approach above
    count = binomialCoeff(2 * N - 1, N);
 
    return count;
 
# Driver Function
if __name__ == "__main__" :
     
    N = 3;
 
    print(count_of_subarrays(N)) ;
 
# This code is contributed by AnkitRai01

// C# program to count non decreasing subarrays
// of size N from N Natural numbers
using System;
 
class GFG
{
 
    // Returns value of Binomial Coefficient C(n, k)
    static int binomialCoeff(int n, int k)
    {
        int []C = new int[k + 1];
     
        // Since nC0 is 1
        C[0] = 1;
     
        for (int i = 1; i <= n; i++)
        {
     
            // Compute next row of pascal triangle using
            // the previous row
            for (int j = Math.Min(i, k); j > 0; j--)
                C[j] = C[j] + C[j - 1];
        }
        return C[k];
    }
     
    // Function to find the count of required subarrays
    static int count_of_subarrays(int N)
    {
     
        // The required count is the binomial coefficient
        // as explained in the approach above
        int count = binomialCoeff(2 * N - 1, N);
     
        return count;
    }
     
    // Driver Function
    public static void Main()
    {
        int N = 3;
        Console.WriteLine(count_of_subarrays(N));
    }
}
 
// This code is contributed by AnkitRai01

<script>
 
// Javascript program to count non decreasing subarrays
// of size N from N Natural numbers
 
// Returns value of Binomial Coefficient C(n, k)
function binomialCoeff(n, k)
{
    var C = Array(k+1).fill(0);
 
    // Since nC0 is 1
    C[0] = 1;
 
    for (var i = 1; i <= n; i++) {
 
        // Compute next row of pascal triangle using
        // the previous row
        for (var j = Math.min(i, k); j > 0; j--)
            C[j] = C[j] + C[j - 1];
    }
    return C[k];
}
 
// Function to find the count of required subarrays
function count_of_subarrays(N)
{
 
    // The required count is the binomial coefficient
    // as explained in the approach above
    var count = binomialCoeff(2 * N - 1, N);
 
    return count;
}
 
// Driver Function
var N = 3;
document.write( count_of_subarrays(N));
 
// This code is contributed by itsok.
</script>

10

Complejidad del tiempo: O(N ² )

Espacio Auxiliar: O(N)