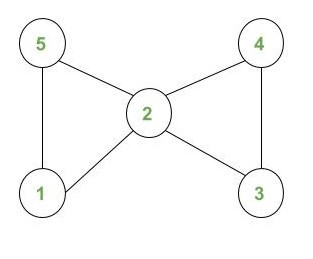
Dado un gráfico no dirigido con Nodes V (por ejemplo, numerados de 1 a V) y aristas E , la tarea es verificar si el gráfico es un gráfico de Euler o no y, de ser así, convertirlo en un circuito de Euler dirigido.
Un circuito de Euler dirigido es un gráfico dirigido tal que si comienza a atravesar el gráfico desde cualquier Node y viaja a través de cada borde exactamente una vez, terminará en el Node inicial.
Nota: Al atravesar un circuito de Euler, cada arista se atraviesa exactamente una vez. Un Node se puede atravesar más de una vez si es necesario, pero un borde no se puede atravesar más de una vez.
Ejemplo:
Aporte:
Salida:
1 2
2 5
5 1
2 4
4 3
3 2
Explicación:
El circuito de Euler dirigido para el gráfico no dirigido dado será:
Acercarse:
- Primero, debemos asegurarnos de que el gráfico no dirigido dado sea euleriano o no . Si el grafo no dirigido no es euleriano, no podemos convertirlo en un grafo euleriano dirigido.
- Para comprobarlo solo necesitamos calcular el grado de cada Node. Si el grado de todos los Nodes es par y no igual a 0, entonces el gráfico es Euleriano.
- Usaremos Profundidad de búsqueda transversal primero para asignar las direcciones.
- Durante el recorrido estableceremos la dirección de un borde de padre a hijo. Mantendremos un mapa para asegurarnos de que un borde se cruce solo una vez.
A continuación se muestra la implementación del algoritmo anterior:
C++
// C++ program to Convert an
// Undirected Graph to a
// Directed Euler Circuit
#include <bits/stdc++.h>
using namespace std;
vector<int> g[100];
// Array to store degree
// of nodes.
int deg[100] = { 0 };
// Map to keep a track of
// visited edges
map<pair<int, int>, int> m1;
// Vector to store the edge
// pairs
vector<pair<int, int> > v;
// Function to add Edge
void addEdge(int u, int v)
{
deg[u]++;
deg[v]++;
g[u].push_back(v);
g[v].push_back(u);
}
// Function to check if graph
// is Eulerian or not
bool CheckEulerian(int n)
{
int check = 0;
for (int i = 1; i <= n; i++) {
// Checking if odd degree
// or zero degree nodes
// are present
if (deg[i] % 2 || deg[i] == 0) {
check = 1;
break;
}
}
// If any degree is odd or
// any vertex has degree 0
if (check) {
return false;
}
return true;
}
// DFS Function to assign the direction
void DirectedEuler(int node,
vector<int> g[])
{
for (auto i = g[node].begin();
i != g[node].end(); i++) {
// Checking if edge is already
// visited
if (m1[make_pair(node, *i)]
|| m1[make_pair(*i, node)])
continue;
m1[make_pair(node, *i)]++;
// Storing the edge
v.push_back(make_pair(node, *i));
DirectedEuler(*i, g);
}
}
// Function prints the convert
// Directed graph
void ConvertDirectedEuler(int n,
int e)
{
if (!CheckEulerian(n)) {
cout << "NOT POSSIBLE"
<< endl;
return;
}
DirectedEuler(1, g);
// Printing directed edges
for (auto i = v.begin();
i != v.end(); i++) {
cout << (*i).first
<< " "
<< (*i).second
<< endl;
}
}
// Driver code
int main()
{
int N = 5;
int E = 6;
addEdge(1, 2);
addEdge(1, 5);
addEdge(5, 2);
addEdge(2, 4);
addEdge(2, 3);
addEdge(4, 3);
ConvertDirectedEuler(N, E);
}
Java
// Java program to Convert an
// Undirected Graph to a
// Directed Euler Circuit
import java.io.*;
import java.lang.*;
import java.util.*;
class GFG{
// Pair class to store Key in map
static class Pair
{
int first;
int second;
Pair(int first, int second)
{
this.first = first;
this.second = second;
}
@Override
public int hashCode()
{
final int prime = 31;
int result = 1;
result = prime * result + first;
result = prime * result + second;
return result;
}
@Override
public boolean equals(Object obj)
{
if (this == obj)
return true;
if (obj == null)
return false;
if (getClass() != obj.getClass())
return false;
Pair other = (Pair) obj;
if (first != other.first)
return false;
if (second != other.second)
return false;
return true;
}
}
// To store graph
static ArrayList<Integer> g[];
// Array to store degree of nodes.
static int deg[];
// Vector to store the edge pairs
static ArrayList<Pair> v;
// Map to keep a track of
// visited edges
static HashMap<Pair, Integer> m1;
@SuppressWarnings("unchecked")
static void initialize()
{
g = new ArrayList[100];
for(int i = 0; i < 100; i++)
g[i] = new ArrayList<>();
deg = new int[100];
v = new ArrayList<>();
m1 = new HashMap<>();
}
// Function to add Edge
static void addEdge(int u, int v)
{
deg[u]++;
deg[v]++;
g[u].add(v);
g[v].add(u);
}
// Function to check if graph
// is Eulerian or not
static boolean CheckEulerian(int n)
{
int check = 0;
for(int i = 1; i <= n; i++)
{
// Checking if odd degree
// or zero degree nodes
// are present
if (deg[i] % 2 == 1 || deg[i] == 0)
{
check = 1;
break;
}
}
// If any degree is odd or
// any vertex has degree 0
if (check == 1)
{
return false;
}
return true;
}
// DFS Function to assign the direction
static void DirectedEuler(int node,
ArrayList<Integer> g[])
{
for(int i : g[node])
{
// Checking if edge is already
// visited
if (m1.containsKey(new Pair(node, i)) ||
m1.containsKey(new Pair(i, node)))
continue;
m1.put(new Pair(node, i), 1);
// Storing the edge
v.add(new Pair(node, i));
DirectedEuler(i, g);
}
}
// Function prints the convert
// Directed graph
static void ConvertDirectedEuler(int n, int e)
{
if (!CheckEulerian(n))
{
System.out.println("NOT POSSIBLE");
return;
}
DirectedEuler(1, g);
// Printing directed edges
for(Pair p : v)
{
System.out.println(p.first + " " + p.second);
}
}
// Driver Code
public static void main(String[] args)
{
int N = 5;
int E = 6;
// To initialize
initialize();
addEdge(1, 2);
addEdge(1, 5);
addEdge(5, 2);
addEdge(2, 4);
addEdge(2, 3);
addEdge(4, 3);
ConvertDirectedEuler(N, E);
}
}
// This code is contributed by Kingash
Python3
# Python program to Convert an
# Undirected Graph to a
# Directed Euler Circuit
from typing import List
g = [[] for _ in range(100)]
# Array to store degree
# of nodes.
deg = [0 for _ in range(100)]
# Map to keep a track of
# visited edges
m1 = dict()
# Vector to store the edge
# pairs
v = []
# Function to add Edge
def addEdge(u: int, v: int) -> None:
global deg, g
deg[u] += 1
deg[v] += 1
g[u].append(v)
g[v].append(u)
# Function to check if graph
# is Eulerian or not
def CheckEulerian(n: int) -> bool:
check = 0
for i in range(1, n + 1):
# Checking if odd degree
# or zero degree nodes
# are present
if (deg[i] % 2 or deg[i] == 0):
check = 1
break
# If any degree is odd or
# any vertex has degree 0
if (check):
return False
return True
# DFS Function to assign the direction
def DirectedEuler(node: int, g: List[List[int]]) -> None:
for i in g[node]:
# Checking if edge is already
# visited
if ((node, i) in m1 or (i, node) in m1):
continue
if (node, i) not in m1:
m1[(node, i)] = 0
m1[(node, i)] += 1
# Storing the edge
v.append((node, i))
DirectedEuler(i, g)
# Function prints the convert
# Directed graph
def ConvertDirectedEuler(n: int, e: int) -> None:
if (not CheckEulerian(n)):
print("NOT POSSIBLE")
return
DirectedEuler(1, g)
# Printing directed edges
for i in v:
print("{} {}".format(i[0], i[1]))
# Driver code
if __name__ == "__main__":
N = 5
E = 6
addEdge(1, 2)
addEdge(1, 5)
addEdge(5, 2)
addEdge(2, 4)
addEdge(2, 3)
addEdge(4, 3)
ConvertDirectedEuler(N, E)
# This code is contributed by sanjeev2552
C#
// C# program to Convert an
// Undirected Graph to a
// Directed Euler Circuit
using System;
using System.Collections.Generic;
class GFG {
static List<List<int>> g = new List<List<int>>();
// Array to store degree
// of nodes.
static int[] deg = new int[100];
// Map to keep a track of
// visited edges
static Dictionary<Tuple<int,int>, int> m1 = new Dictionary<Tuple<int,int>, int>();
// Vector to store the edge
// pairs
static List<Tuple<int,int>> v = new List<Tuple<int,int>>();
// Function to add Edge
static void addEdge(int u, int v)
{
deg[u]++;
deg[v]++;
g[u].Add(v);
g[v].Add(u);
}
// Function to check if graph
// is Eulerian or not
static bool CheckEulerian(int n)
{
int check = 0;
for (int i = 1; i <= n; i++) {
// Checking if odd degree
// or zero degree nodes
// are present
if (deg[i] % 2 != 0 || deg[i] == 0) {
check = 1;
break;
}
}
// If any degree is odd or
// any vertex has degree 0
if (check == 1) {
return false;
}
return true;
}
// DFS Function to assign the direction
static void DirectedEuler(int node, List<List<int>> g)
{
int[,] m = {{1, 2}, {2, 5}, {5, 1}, {2, 4}, {4, 3}, {3, 2}};
for(int i = 0; i < g[node].Count; i++) {
// Checking if edge is already
// visited
if (!m1.ContainsKey(new Tuple<int,int>(node, g[node][i]))
|| !m1.ContainsKey(new Tuple<int,int>(g[node][i], node)))
continue;
m1[new Tuple<int,int>(node, g[node][i])] = 1;
// Storing the edge
v.Add(new Tuple<int,int>(node, g[node][i]));
DirectedEuler(g[node][i], g);
}
for(int i = 0; i < m.GetLength(0); i++)
{
Console.WriteLine(m[i,0] + " " + m[i,1]);
}
}
// Function prints the convert
// Directed graph
static void ConvertDirectedEuler(int n, int e)
{
if (!CheckEulerian(n)) {
Console.Write("NOT POSSIBLE");
return;
}
DirectedEuler(1, g);
// Printing directed edges
for (int i = 0; i < v.Count; i++) {
Console.WriteLine(v[i].Item1 + " " + v[i].Item2);
}
}
static void Main() {
for(int i = 0; i < 100; i++)
{
g.Add(new List<int>());
}
int N = 5;
int E = 6;
addEdge(1, 2);
addEdge(1, 5);
addEdge(5, 2);
addEdge(2, 4);
addEdge(2, 3);
addEdge(4, 3);
ConvertDirectedEuler(N, E);
}
}
// This code is contributed by suresh07.
Javascript
<script>
// Javascript program to Convert an
// Undirected Graph to a
// Directed Euler Circuit
let g = [];
for(let i = 0; i < 100; i++)
{
g.push([]);
}
// Array to store degree
// of nodes.
let deg = new Array(100);
deg.fill(0);
// Map to keep a track of
// visited edges
let m1 = new Map();
// Vector to store the edge
// pairs
let v = [];
// Function to add Edge
function addEdge(u, v)
{
deg[u]++;
deg[v]++;
g[u].push(v);
g[v].push(u);
}
// Function to check if graph
// is Eulerian or not
function CheckEulerian(n)
{
let check = 0;
for (let i = 1; i <= n; i++) {
// Checking if odd degree
// or zero degree nodes
// are present
if (deg[i] % 2 != 0 || deg[i] == 0) {
check = 1;
break;
}
}
// If any degree is odd or
// any vertex has degree 0
if (check == 1) {
return false;
}
return true;
}
// DFS Function to assign the direction
function DirectedEuler(node, g)
{
let m = [[1, 2], [2, 5], [5, 1], [2, 4], [4, 3], [3, 2]];
for(let i = 0; i < g[node].length; i++) {
// Checking if edge is already
// visited
if (!m1.has([node, g[node][i]])
|| !m1.has([g[node][i], node]))
continue;
m1.set([node, g[node][i]], 1);
// Storing the edge
v.push([node, g[node][i]]);
DirectedEuler(g[node][i], g);
}
for(let i = 0; i < m.length; i++)
{
document.write(m[i][0] + " " + m[i][1] + "</br>");
}
}
// Function prints the convert
// Directed graph
function ConvertDirectedEuler(n, e)
{
if (!CheckEulerian(n)) {
document.write("NOT POSSIBLE");
return;
}
DirectedEuler(1, g);
// Printing directed edges
for (let i = 0; i < v.length; i++) {
document.write(v[i][0] + " " + v[i][1] + "</br>");
}
}
let N = 5;
let E = 6;
addEdge(1, 2);
addEdge(1, 5);
addEdge(5, 2);
addEdge(2, 4);
addEdge(2, 3);
addEdge(4, 3);
ConvertDirectedEuler(N, E);
// This code is contributed by divyesh072019.
</script>
1 2 2 5 5 1 2 4 4 3 3 2
Complejidad de tiempo: O(( V + E ) * log( E ))
Complejidad de espacio: O(max( V, E ))
Publicación traducida automáticamente
Artículo escrito por akarshan2000 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA