Dados dos arreglos X[] y H[] de longitud N y M respectivamente, la tarea es encontrar la convolución circular de los arreglos dados usando el método Matrix. La multiplicación de la array desplazada circularmente y el vector de columna es la convolución circular de las arrays.
Ejemplos:
Entrada: X[] = {1, 2, 4, 2}, H[] = {1, 1, 1}
Salida: 7 5 7 8
Entrada: X[] = {5, 7, 3, 2}, H [] = {1, 5}
Salida: 15 32 38 17
Explicación:
- Cree una array desplazada circularmente circular_shift_mat de K * K usando los elementos de la array cuya longitud es máxima (X n en este caso) donde K es MAX (N, M).
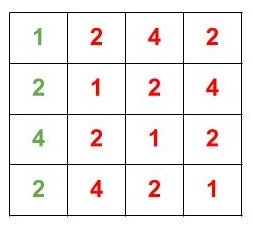
Array desplazada circularmente de la array X n .
- Cree un vector-columna col_vec de longitud K
- Inserte los elementos de la array H m en el col_vec en las posiciones [0, m).
- Como K = max(N, M), aquí N; M < K. Por lo tanto, complete el resto de las posiciones de col_vec [m, K) con 0. Por lo tanto, col_vec será
col_vec = { 1, 1, 1, 0 }
- Multiplique el circular_shift_mat y el col_vec
- La multiplicación de la array desplazada circularmente (circular_shift_mat) y el vector de columna (col_vec) es la convolución circular de las arrays.
Acercarse:
- Cree una Array desplazada circularmente de N * N usando los elementos de la array de la longitud máxima.
- Cree un vector de columna de longitud N usando elementos de otra array y complete el resto de las posiciones por 0.
- La multiplicación de Matrix y el vector de columna es la convolución circular de arrays.
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ program to compute circular
// convolution of two arrays
#include <bits/stdc++.h>
using namespace std;
#define MAX_SIZE 10
// Function to find circular convolution
void convolution(vector<int>& x, vector<int>& h, int n, int m)
{
int row_vec[MAX_SIZE], col_vec[MAX_SIZE];
int out[MAX_SIZE] = { 0 };
int circular_shift_mat[MAX_SIZE][MAX_SIZE];
// Finding the maximum size between the
// two input sequence sizes
int maxSize = n > m ? n : m;
// Copying elements of x to row_vec and padding
// zeros if size of x < maxSize
for (int i = 0; i < maxSize; i++) {
if (i >= n) {
row_vec[i] = 0;
}
else {
row_vec[i] = x[i];
}
}
// Copying elements of h to col_vec and padding
// zeros if size of h is less than maxSize
for (int i = 0; i < maxSize; i++) {
if (i >= m) {
col_vec[i] = 0;
}
else {
col_vec[i] = h[i];
}
}
// Generating 2D matrix of
// circularly shifted elements
int k = 0, d = 0;
for (int i = 0; i < maxSize; i++) {
int curIndex = k - d;
for (int j = 0; j < maxSize; j++) {
circular_shift_mat[j][i] = row_vec
[curIndex % maxSize];
curIndex++;
}
k = maxSize;
d++;
}
// Computing result by matrix
// multiplication and printing results
for (int i = 0; i < maxSize; i++) {
for (int j = 0; j < maxSize; j++) {
out[i] += circular_shift_mat[i][j]
* col_vec[j];
}
cout << out[i] << " ";
}
}
// Driver program
int main()
{
vector<int> x = { 5, 7, 3, 2 };
int n = x.size();
vector<int> h = { 1, 5 };
int m = h.size();
convolution(x, h, n, m);
return 0;
}
Java
// Java program to compute circular
// convolution of two arrays
class GFG
{
final static int MAX_SIZE = 10 ;
// Function to find circular convolution
static void convolution(int []x, int []h, int n, int m)
{
int row_vec[] = new int[MAX_SIZE];
int col_vec[] = new int[MAX_SIZE];
int out[] = new int [MAX_SIZE];
int circular_shift_mat[][] = new int[MAX_SIZE][MAX_SIZE];
// Finding the maximum size between the
// two input sequence sizes
int maxSize = n > m ? n : m;
// Copying elements of x to row_vec and padding
// zeros if size of x < maxSize
for (int i = 0; i < maxSize; i++)
{
if (i >= n)
{
row_vec[i] = 0;
}
else
{
row_vec[i] = x[i];
}
}
// Copying elements of h to col_vec and padding
// zeros if size of h is less than maxSize
for (int i = 0; i < maxSize; i++)
{
if (i >= m)
{
col_vec[i] = 0;
}
else
{
col_vec[i] = h[i];
}
}
// Generating 2D matrix of
// circularly shifted elements
int k = 0, d = 0;
for (int i = 0; i < maxSize; i++)
{
int curIndex = k - d;
for (int j = 0; j < maxSize; j++)
{
circular_shift_mat[j][i] =
row_vec[curIndex % maxSize];
curIndex++;
}
k = maxSize;
d++;
}
// Computing result by matrix
// multiplication and printing results
for (int i = 0; i < maxSize; i++)
{
for (int j = 0; j < maxSize; j++)
{
out[i] += circular_shift_mat[i][j] * col_vec[j];
}
System.out.print(out[i] + " ");
}
}
// Driver program
public static void main (String[] args)
{
int x[] = { 5, 7, 3, 2 };
int n = x.length;
int h[] = { 1, 5 };
int m = h.length;
convolution(x, h, n, m);
}
}
// This code is contributed by AnkitRai01
Python3
# Python program to compute circular # convolution of two arrays MAX_SIZE = 10; # Function to find circular convolution def convolution(x, h, n, m): row_vec = [0] * MAX_SIZE; col_vec = [0] * MAX_SIZE; out = [0] * MAX_SIZE; circular_shift_mat = [[0 for i in range(MAX_SIZE)] for j in range(MAX_SIZE)] ; # Finding the maximum size between the # two input sequence sizes if(n > m ): maxSize = n; else: maxSize = m; # Copying elements of x to row_vec and padding # zeros if size of x < maxSize for i in range(maxSize): if (i >= n): row_vec[i] = 0; else: row_vec[i] = x[i]; # Copying elements of h to col_vec and padding # zeros if size of h is less than maxSize for i in range(maxSize): if (i >= m): col_vec[i] = 0; else: col_vec[i] = h[i]; # Generating 2D matrix of # circularly shifted elements k = 0; d = 0; for i in range(maxSize): curIndex = k - d; for j in range(maxSize): circular_shift_mat[j][i] = \ row_vec[curIndex % maxSize]; curIndex += 1; k = maxSize; d += 1; # Computing result by matrix # multiplication and printing results for i in range(maxSize): for j in range(maxSize): out[i] += circular_shift_mat[i][j] * \ col_vec[j]; print(out[i], end = " "); # Driver program if __name__ == '__main__': x = [ 5, 7, 3, 2 ]; n = len(x); h = [ 1, 5 ]; m = len(h); convolution(x, h, n, m); # This code is contributed by 29AjayKumar
C#
// C# program to compute circular
// convolution of two arrays
using System;
class GFG
{
readonly static int MAX_SIZE = 10 ;
// Function to find circular convolution
static void convolution(int []x, int []h,
int n, int m)
{
int []row_vec = new int[MAX_SIZE];
int []col_vec = new int[MAX_SIZE];
int []out_ = new int [MAX_SIZE];
int [,]circular_shift_mat =
new int[MAX_SIZE,MAX_SIZE];
// Finding the maximum size between the
// two input sequence sizes
int maxSize = n > m ? n : m;
// Copying elements of x to row_vec and padding
// zeros if size of x < maxSize
for (int i = 0; i < maxSize; i++)
{
if (i >= n)
{
row_vec[i] = 0;
}
else
{
row_vec[i] = x[i];
}
}
// Copying elements of h to col_vec and padding
// zeros if size of h is less than maxSize
for (int i = 0; i < maxSize; i++)
{
if (i >= m)
{
col_vec[i] = 0;
}
else
{
col_vec[i] = h[i];
}
}
// Generating 2D matrix of
// circularly shifted elements
int k = 0, d = 0;
for (int i = 0; i < maxSize; i++)
{
int curIndex = k - d;
for (int j = 0; j < maxSize; j++)
{
circular_shift_mat[j, i] =
row_vec[curIndex % maxSize];
curIndex++;
}
k = maxSize;
d++;
}
// Computing result by matrix
// multiplication and printing results
for (int i = 0; i < maxSize; i++)
{
for (int j = 0; j < maxSize; j++)
{
out_[i] += circular_shift_mat[i, j] *
col_vec[j];
}
Console.Write(out_[i] + " ");
}
}
// Driver program
public static void Main(String[] args)
{
int []x = {5, 7, 3, 2};
int n = x.Length;
int []h = {1, 5};
int m = h.Length;
convolution(x, h, n, m);
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// JavaScript program to compute circular
// convolution of two arrays
let MAX_SIZE = 10 ;
// Function to find circular convolution
function convolution(x, h, n, m)
{
let row_vec = new Array(MAX_SIZE);
row_vec.fill(0);
let col_vec = new Array(MAX_SIZE);
col_vec.fill(0);
let out = new Array(MAX_SIZE);
out.fill(0);
let circular_shift_mat = new Array(MAX_SIZE);
circular_shift_mat.fill(0);
for (let i = 0; i < MAX_SIZE; i++)
{
circular_shift_mat[i] = new Array(MAX_SIZE);
for (let j = 0; j < MAX_SIZE; j++)
{
circular_shift_mat[i][j] = 0;
}
}
// Finding the maximum size between the
// two input sequence sizes
let maxSize = n > m ? n : m;
// Copying elements of x to row_vec and padding
// zeros if size of x < maxSize
for (let i = 0; i < maxSize; i++)
{
if (i >= n)
{
row_vec[i] = 0;
}
else
{
row_vec[i] = x[i];
}
}
// Copying elements of h to col_vec and padding
// zeros if size of h is less than maxSize
for (let i = 0; i < maxSize; i++)
{
if (i >= m)
{
col_vec[i] = 0;
}
else
{
col_vec[i] = h[i];
}
}
// Generating 2D matrix of
// circularly shifted elements
let k = 0, d = 0;
for (let i = 0; i < maxSize; i++)
{
let curIndex = k - d;
for (let j = 0; j < maxSize; j++)
{
circular_shift_mat[j][i] =
row_vec[curIndex % maxSize];
curIndex++;
}
k = maxSize;
d++;
}
// Computing result by matrix
// multiplication and printing results
for (let i = 0; i < maxSize; i++)
{
for (let j = 0; j < maxSize; j++)
{
out[i] += circular_shift_mat[i][j] * col_vec[j];
}
document.write(out[i] + " ");
}
}
let x = [ 5, 7, 3, 2 ];
let n = x.length;
let h = [ 1, 5 ];
let m = h.length;
convolution(x, h, n, m);
</script>
Producción:
15 32 38 17
Complejidad de tiempo: O(MAX_SIZE * MAX_SIZE)
Espacio auxiliar: O(MAX_SIZE * MAX_SIZE)