Convolución continua del kernel

La convolución de núcleo continuo fue propuesta por el investigador de la Universidad Verije de Ámsterdam en colaboración con la Universidad de Ámsterdam en un artículo titulado ‘ CKConv: Convolución de núcleo continuo para datos secuenciales ‘. La motivación detrás de esto es proponer un modelo que utilice las propiedades de las redes neuronales de convolución y las redes neuronales recurrentes para procesar una larga secuencia de datos de imágenes.

Operación de convolución

Sean x ∶R → R ^N_^c y ψ ∶ R → R ^N_^c una señal de valor vectorial y kernel en R, tal que x = {x _c } ^Nc y ψ = {ψ _c } N _C c=1. La operación de convolución se puede definir como:

$(x * \psi)(t) = \sum_{c=1}^{N_c} \int_\mathbb{R} x_c(\tau)\psi_c(t-\tau)d\tau$

Sin embargo, prácticamente la señal de entrada x se obtiene del muestreo. Por lo tanto, la señal de entrada y la convolución se pueden definir como

Señal de entrada : $\chi = {x(\tau )}_{\tau=0}^{N_x}$
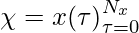
Convolución : $\kappa = {\psi(\tau)}_{\tau=0}^{N_x}$

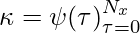
y la ecuación que está centrada alrededor de t está dada por:

$(\chi * \psi)(t) = \sum_{c=1}^{N_c} \sum_{\tau = 0}^{t}x_c\left ( \tau \right )\psi_c\left ( t-\tau \right )$

Ahora, para la convolución del kernel continuo, usaremos un kernel de convolución ψ como función continua parametrizada sobre un pequeño NN llamado MLP ^ψ . Toma (t−τ) como entrada y genera el valor del kernel de convolución en esa posición ψ(t−τ ). El kernel continuo puede ser formulado por:

$(\chi * \psi)(t) = \sum_{c=1}^{N_c} \sum_{\tau = 0}^{t}x_c\left ( \tau \right )MLP^{\psi_c}\left ( t-\tau \right )$

Si el factor de muestreo es diferente del factor de muestreo de entrenamiento, entonces podemos realizar la operación de convolución de las siguientes maneras:

$(\chi * \psi)(t)_{sr2} \approx \frac{sr2}{sr1}(\chi * \psi)(t)_{sr1}$

Unidad Recurrente

Para la secuencia de entrada

$\chi = {x(\tau )}_{\tau=0}^{N_x}$ . The recurrent unit is given by:

$h(\tau) = \sigma(Wh(\tau-1) + U_x(\tau))$

$\tilde{y} (\tau) = softmax (Vh(\tau))$

donde U, W, V son las conexiones de entrada a oculto, oculto a oculto y oculto a salida de la unidad. h(τ ), y˜(τ ) representan la representación oculta y la salida en el paso de tiempo τ, y σ representa una no linealidad puntual.

Ahora, desarrollamos la ecuación anterior para t pasos:

$h(t) = W^{t+1}h(-1) + \sum_{\tau =0 } ^{t} W^{\tau} U x(t - \tau)$

donde h(−1) es el estado inicial de la representación oculta. h(t) también se puede representar de la siguiente manera:

$x =[x(0), x(1), x(2) .....x(t-1),x(t)] \\ \psi =[U, WU, .... W^{t-1}U, W^{t}U] \\ h(t) = \sum_{\tau =0 }^{t}x(\tau)\psi(t-\tau) + \sum_{\tau =0 }^{t}x(t - \tau)\psi(\tau)$

La ecuación anterior nos proporciona la siguiente conclusión:

El problema del gradiente de fuga y el gradiente de explosión en RNN es causado por el término x(t-τ) τ retrocede en el pasado y se multiplica con un peso de convolución efectivo ψ(τ )=W ^τ U.
La unidad recurrente lineal se puede definir como la convolución de las funciones de convolución de entrada y exponencial.

Núcleo continuo MLP

Sea {∆t _i =(t − τ _i )} ^N i=0 una secuencia de posiciones relativas. El kernel de convolución MLP _ψ está parametrizado por una red neuronal de capa L convencional:

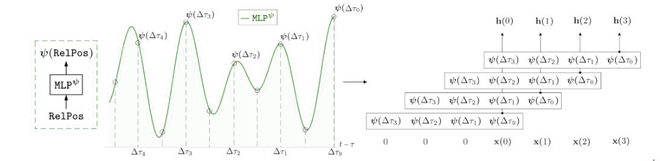
MLP

$h^{(1)}(\Delta \tau_i ) = \sigma\left ( w^{1} \Delta \tau_i + b^{(1)} \right ) \\ h^{(1)}(\Delta \tau_i ) = \sigma\left ( W^{l} * h* (l-1) \Delta \tau_i + b^{(1)} \right ) \\ \psi(\Delta \tau_i) = W^{(L)} * h{(L-1)} (\Delta \tau_i) + b^{(L)}$

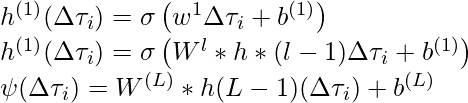
dónde,

$\sigma$ is used to add non-linearity such as ReLU.

Implementación

En esta implementación, entrenaremos el modelo CKconv en el conjunto de datos sMNIST, para esta implementación, usaremos la colaboración que nos proporciona Google.

Python3

# code credits: https://github.com/dwromero/ckconv
# first, we need to clone the ckconv repository from Github
! git clone https://github.com/dwromero/ckconv
 
# Now, we need to change the pwd to ckconv directory
cd ckconv
 
# Before actually train the model,
# we need to first install the required modules and libraries
! pip install -r requirements.txt
 
# if the above command fails, please make sure that following modules installed using
# command below
pip install ml-collections torchaudio mkl-random sktime wandb
 
# Now to train the model on sMNIst dataset, run the following commands
! python run_experiment.py --config.batch_size=64 --config.clip=0 \
--config.dataset=MNIST --config.device=cuda --config.dropout=0.1 \
--config.dropout_in=0.1 --config.epochs=200 --config.kernelnet_activation_function=Sine \
--config.kernelnet_no_hidden=32 --config.kernelnet_norm_type=LayerNorm \
--config.kernelnet_omega_0=31.09195739463897 --config.lr=0.001 --config.model=CKCNN \
--config.no_blocks=2 --config.no_hidden=30 --config.optimizer=Adam \
--config.permuted=False --config.sched_decay_factor=5  --config.sched_patience=20 \
--config.scheduler=plateau

A continuación se muestran los resultados del entrenamiento anterior de CKCNN en datos sMNIST:

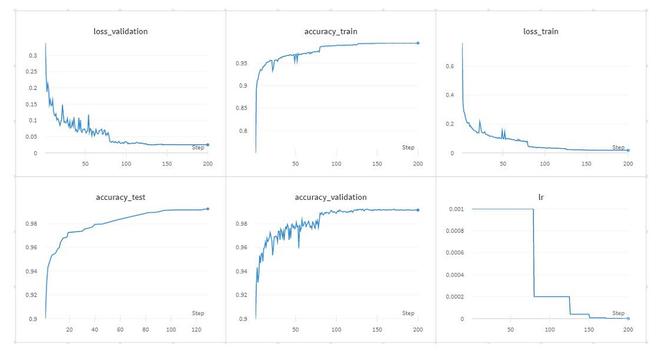
Resultado del entrenamiento de CkConv

Conclusión

Ckconv es capaz de funciones muy complejas y no lineales fácilmente.
A diferencia de las RNN, las CKConv no se basan en ninguna forma de recurrencia para considerar grandes horizontes de memoria y tienen dependencias globales a largo plazo.
Las CKCNN no utilizan la retropropagación a través del tiempo (BPTT). En consecuencia, las CKCNN se pueden entrenar en paralelo.
Las CKCNN también se pueden implementar en resoluciones distintas de la resolución en la que se entrenan.

Referencias:

papel CKConv

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA