Correlación producto-momento de Pearson

El coeficiente de correlación producto-momento de Pearson (o coeficiente de correlación de Pearson) es una medida de la fuerza de una asociación lineal entre dos variables y se denota por r . Básicamente, una correlación producto-momento de Pearson intenta trazar una línea de mejor ajuste a través de los datos de dos variables, y el coeficiente de correlación de Pearson, r , indica qué tan lejos están todos estos puntos de datos de esta línea de mejor ajuste (es decir, qué tan lejos están todos estos puntos de datos de esta línea de mejor ajuste). bien, los puntos de datos se ajustan a este nuevo modelo/línea de mejor ajuste).

Coeficiente de correlación: 

El coeficiente de correlación se puede calcular como la covarianza dividida por la desviación estándar de las variables. La siguiente fórmula se utiliza para calcular la correlación de Pearson (r):

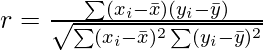
• r= coeficiente de correlación
• x_bar = media de la variable x
• y_bar = media de la variable y.
• x_i, y_i = muestras de la variable x,y

El valor anterior del coeficiente de correlación puede estar entre -1 y 1. Un valor cercano a 1 representa ese grado perfecto de asociación entre las dos variables y se denomina correlación fuerte y un valor cercano a -1 representa la correlación negativa fuerte. El valor más cercano a 0 representa el grado de correlación más débil o nulo.

Una correlación fuertemente positiva (r=1)

Correlación Fuertemente Negativa (r=-1)

Sin correlación (r~=0)

Prueba de Significación: 

Se puede usar una prueba de significancia para el coeficiente de correlación de Pearson para averiguar si la correlación r de Pearson calculada podría haber ocurrido significativamente en la población en la que las dos variables están significativamente relacionadas o no. Las estadísticas de prueba siguen la distribución t con N-2 grados de libertad. La significación se calcula usando la siguiente fórmula

Al realizar la prueba, podemos asumir la siguiente hipótesis:

• Hipótesis Nula : La hipótesis nula podría ser que no existe correlación entre dos variables en un grado dado de significación. Es decir, el valor del coeficiente de correlación de Pearson es cercano a 0.
• Hipótesis alternativa : la hipótesis alternativa supone que el valor del coeficiente de correlación de Pearson es significativamente diferente de 0. Es decir, puede haber alguna correlación entre dos variables.

Pasos para realizar la prueba:

• Establece la hipótesis.
• Decidir el nivel de significación.
• Calcule el grado de libertad (df = N-2) y usando ese valor determine el valor crítico de t de la tabla de distribución t.
• Calcule el coeficiente de correlación de Pearson y calcule el valor de t a partir de la fórmula anterior.
• Determinar si aceptar o rechazar la hipótesis.

Implementación

# imports
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
 
# define the variable
x = np.arange(1,11)
y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 30, 27])
 
# plot the variables
plt.scatter(x,y)
plt.plot(x,y)
 
# the plot above represents a strong correlation.
correlation_coeff, p_value = stats.pearsonr(x,y)
# print pearson correlation coefficient
print(correlation_coeff)
# print p-value: the smallest level of significance that will be enough to reject H0
print(p_value)

Trazado de líneas 

# correlation coefficient
0.960576518918945
# p-value
1.0076332440506521e-05