Dado un árbol binario , la tarea es atravesar el árbol binario en orden de niveles .
Ejemplos:
Input:
1
/ \
2 3
Output:
1
2 3
Input:
5
/ \
2 3
\
6
Output:
5
2 3
6
Enfoque: La idea es utilizar Morris Preorder Traversal para recorrer el árbol en orden de nivel transversal.
Observaciones: Hay principalmente dos observaciones para el recorrido del árbol utilizando el recorrido de preorden de Morris. Eso es –
- En el recorrido Preorder, los Nodes más a la izquierda de un nivel se visitan primero, por lo que se pueden usar para recorrer el árbol en orden de nivel.
- Como mantenemos la distancia horizontal de los Nodes en la vista superior del árbol binario , de manera similar, si mantenemos el nivel del Node actual e incrementamos o disminuimos el nivel según el movimiento, entonces los Nodes se pueden atravesar fácilmente.
Al igual que en el recorrido en preorden de Morris, conectamos el Node más a la derecha del hijo izquierdo con su sucesor en orden para mantener el movimiento de modo que podamos volver al hijo derecho del Node padre después de explorar completamente el hijo izquierdo del padre. Por lo tanto, mientras nos movemos hacia el hijo más a la derecha del hijo izquierdo, podemos hacer un seguimiento del número del incremento en el nivel para calcular el sucesor del nivel en orden del hijo.
A continuación se muestra la explicación del enfoque con la ayuda de un ejemplo:
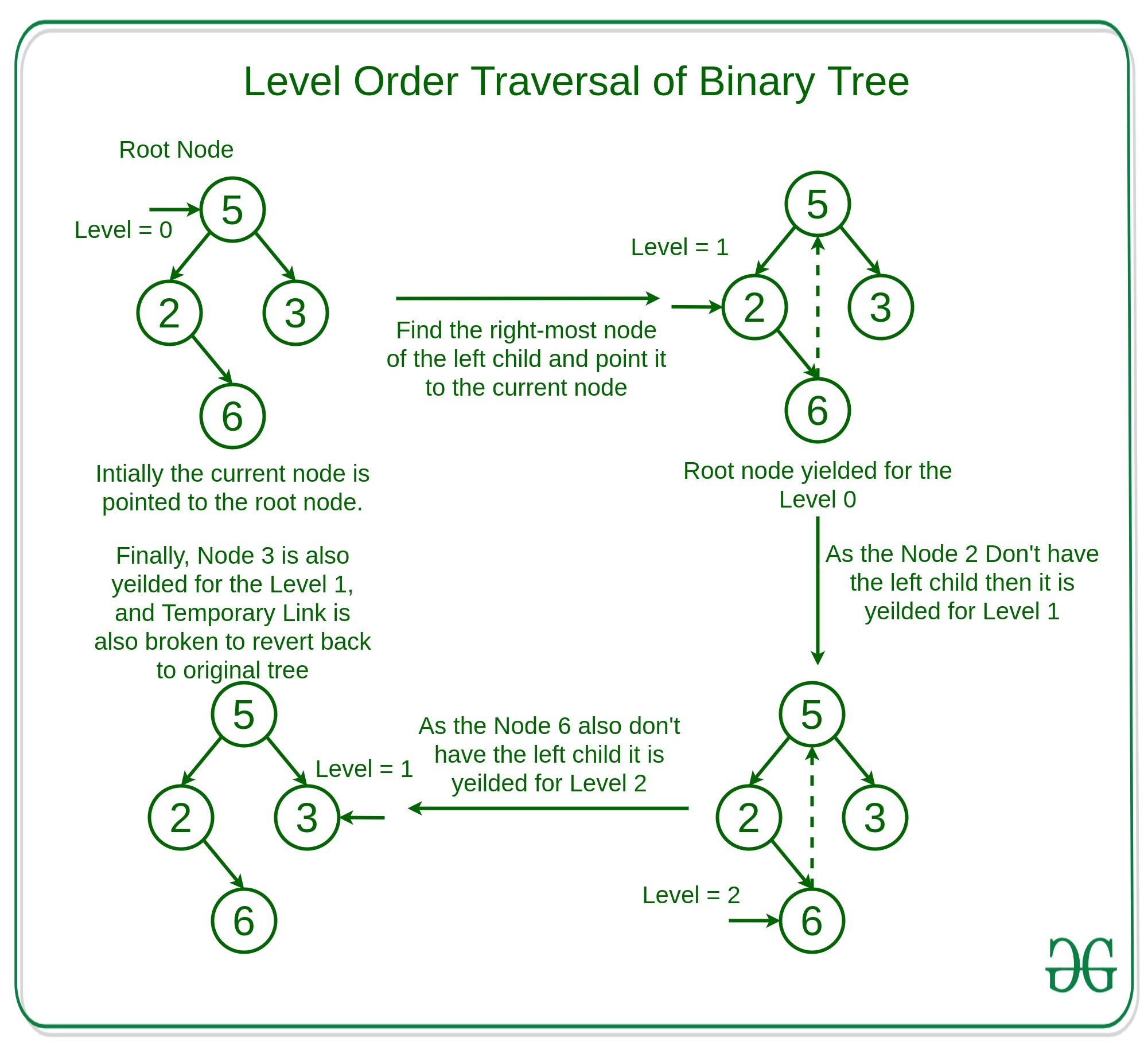
A continuación se muestra la implementación del enfoque anterior:
Python3
# Python implementation of the Level
# order traversal using Morris traversal
# Class of the node of the
# Binary Tree
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Function to traverse the Binary
# tree in the Level Order Fashion
def levelOrderTraversal(root):
# Current Node is marked as
# the Root Node
curr = root
level = 0
# Loop to traverse the Binary
# Tree until the current node
# is not Null
while curr:
# If left child is null, print the
# current node data. And, update
# the current pointer to right child.
if curr.left is None:
# Return the current node with
# its level
yield [curr, level]
curr = curr.right
if curr:
level += 1
else:
level -= 1
else:
# Find the inorder predecessor
prev = curr.left
to_up = 0
# Loop to find the right most
# node of the left child of the
# current node
while prev.right is not None and \
prev.right is not curr:
prev = prev.right
to_up += 1
# If the right child of inorder
# predecessor already points to
# the current node, update the
# current with it's right child
if prev.right is curr:
prev.right = None
curr = curr.right
level -= to_up + 1
# else If right child doesn't
# point to the current node,
# then print this node's data
# and update the right child
# pointer with the current node
# and update the current with
# it's left child
else:
yield [curr, level]
prev.right = curr
curr = curr.left
level += 1
# Driver Code
if __name__ == "__main__":
root = Node(5)
root.left = Node(2)
root.right = Node(3)
root.left.right = Node(6)
# Output List to store the
# Level Order Traversed Nodes
outputData = [[] for i in range(100)]
for node, level in levelOrderTraversal(root):
outputData[level].append(node.data)
h = 0
# Loop to find the height of the
# Binary Tree
for i in outputData:
if i:
h += 1
else:
break
# Loop to print the Data
for i in range(h):
print(' '.join(map(str, outputData[i])))
5 2 3 6
Análisis de rendimiento:
- Complejidad de tiempo: como en el enfoque anterior, cada Node se toca como máximo dos veces, por lo que la complejidad de tiempo es O (N) , donde N es el número de Nodes.
- Espacio auxiliar: como en el enfoque anterior, no se utiliza espacio adicional debido a que el espacio auxiliar utilizado será O(1)
Publicación traducida automáticamente
Artículo escrito por Archit_Dwevedi0 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA