En la vida diaria, las personas a menudo tienen que representar, representar o asociar ciertas cosas u objetos con una cantidad. Esto se debe a que asignar cantidades a ciertos valores o aspectos de la vida facilita compararlos con otros aspectos similares. Por ejemplo, un maestro que califica los trabajos de los estudiantes no etiquetaría cada trabajo con adjetivos como «bueno», «mejor», «impresionante» o «pobre», etc., sino que asignaría un cierto valor numérico a ese trabajo en función de la calificación del estudiante. rendimiento, de modo que es fácil evaluar el nivel de conocimiento y preparación del alumno, pero si se aplicara el enfoque anterior, se generaría una confusión total y no se podría hacer una comparación precisa de él. Dado que en algún momento, el maestro se quedaría sin adjetivos que son relevantes para esta situación particular, y llevaría a que se usen las mismas palabras para calificar todas las respuestas únicas dadas por los estudiantes. Situaciones como estas exigen, más bien, requieren el uso de un método único de valoración, que no solo ayuda a reconocer el verdadero valor del objeto en cuestión, sino que también lo representa de manera justa y sin ambigüedades. Tal sistema que usa ciertas palabras o símbolos para cuantificar un objeto o valor dado se llama sistema numérico.
Número
Un número se refiere a una palabra o símbolo que representa una cantidad particular. Es solo con la ayuda de los números que se realizan múltiples operaciones aritméticas y hemos podido desarrollar tanto en el campo de la física y las matemáticas. Uno no puede vivir su vida sin el uso de números, incluso para las tareas o tareas más básicas. Incluso el dinero intercambiado por mercancías es un cierto valor representado por números. Se utiliza un grupo de números agrupados para asignar a una persona como su número de contacto. tal es el protagonismo de los números en nuestras vidas. Por lo tanto, es imperativo saber más sobre los números y los sistemas numéricos, como se analiza a continuación.
Contando numeros
Un conjunto de números como el que se usa para contar ciertos objetos se llama números de conteo. Tal conjunto de números comienza con 1 (uno) y continúa hasta el infinito. Uno aquí representa un solo objeto. Por ejemplo, el Sr. A tenía un lápiz y un bolígrafo en la mano, o hoy comí un plátano. La suma de dos números contables produce otro número contable. Estos se utilizan en la vida real para intercambio básico, cálculos y operaciones.
el numero cero
Cero se denota por 0. Se utiliza para representar nada. En otras palabras, si algo no tiene ningún valor, se le asigna el número cero como cantidad. El número cero viene antes de todos los números de conteo y forma el conjunto de ‘números enteros’.
Los diferentes tipos de números en matemáticas,
- Números naturales Un conjunto de números que se utilizan para contar ciertos objetos se denominan números naturales. Tal conjunto de números comienza con 1 (uno) y continúa hasta el infinito. Cabe señalar que los números naturales incluyen solo números enteros positivos.
- Números Enteros Un conjunto de números que incluye todos los enteros positivos y el cero.
- Números enteros Un número entero se define como un número entero que puede asumir un valor positivo, negativo o ningún valor.
- Números reales Tales números que incluyen tanto números racionales como sus contrapartes irracionales.
- Números racionales Estos números se pueden expresar en forma de fracción.
- Números irracionales Dichos números no se pueden expresar como una fracción.
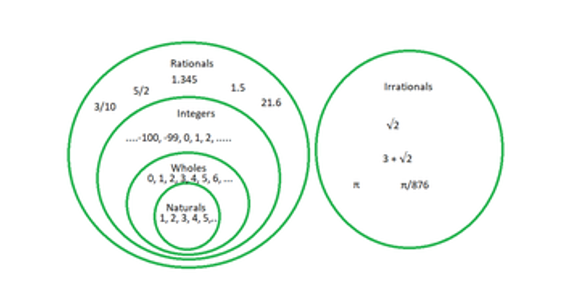
El siguiente diagrama muestra todos los tipos de números discutidos hasta ahora,
Además de los tipos mencionados anteriormente, también tenemos las siguientes categorías de números,
- Números pares Los números que se pueden dividir por 2 se llaman números pares. Ejemplo: 2, 4, 6, 8, …, 1024, etc.
- Números impares Los números que no son divisibles por 2 se llaman números impares. Ejemplo: 3, 5, 7, 10, …, 1345, etc.
- Números primos Un número que se puede dividir exactamente por sí mismo o por 1. Ejemplo: 5, 7, 13, 23, etc.
- Números compuestos Números que tienen múltiples factores distintos de 1 y el número en sí. Ejemplo: 16, 20, 50, etc.
Sistema de numeración
Está claro que los números se utilizan para representar una cierta cantidad. Cuando se usan ciertos símbolos o dígitos para representar los números mismos, se forma un sistema numérico. Por lo tanto, un sistema numérico es un sistema que puede usarse para definir un conjunto de valores, que luego se usan para representar una cantidad.
Tipos de sistemas numéricos
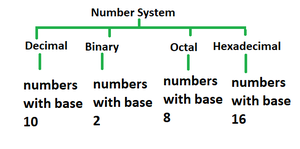
Hay varios tipos de sistemas numéricos en matemáticas. Los cuatro tipos de sistemas numéricos más comunes son:
- Sistema de números decimales
- Sistema numérico binario
- Sistema de numeración octal
- sistema numérico hexadecimal
Sistema de números decimales
Tal sistema numérico que tiene un valor base de 10 se denomina sistema numérico decimal. Utiliza los dígitos entre 0 – 9 para la creación de números. En este sistema, cada dígito se representa como su producto con diferentes potencias de 10. Otra característica a tener en cuenta es que el valor posicional sigue aumentando de derecha a izquierda, con el extremo derecho denominado como unidades, luego decenas, centenas, miles, y así. El lugar de las unidades (unidades) se representaría como 10 0 , las decenas serían 10 1 , las centenas 10 2 , y así sucesivamente.
Por ejemplo: 548 tiene valores posicionales como
(5 x 10 2 ) + ( 4 x 10 1 ) + (8 x 10 0 )
= 5×100 + 4×10 + 8×1
= 500 + 40 + 8
= 548
Sistema de números binarios
Como sugiere el nombre, este tipo de sistema numérico tiene un valor base de 2 (binario). Este sistema utiliza sólo dos dígitos, es decir, 0 y 1 para crear números. Ampliamente utilizado en aplicaciones informáticas, este sistema es realmente fácil de utilizar. Por ejemplo:
14 se puede escribir como 1110
50 se puede escribir como 110010
Sistema de numeración octal
Como sugiere el nombre, este sistema tiene un valor base de 8 (octal). Por lo tanto, utiliza 8 dígitos para crear números. Por ejemplo:
(112) 10 se puede expresar como (287) 8 .
(287) 10 se puede expresar como (372) 8 .
Sistema numérico hexadecimal
Este sistema tiene un valor base de 16 y, por lo tanto, utiliza 16 dígitos para la creación de números. Por ejemplo:
(255) 10 se puede escribir como (FF) 16
(1096) 10 se puede escribir como (448) 16
(4090) 10 se puede escribir como (FFA) 16
¿Cuál es la importancia del sistema numérico?
Es seguro y sabio estar de acuerdo en que el sistema numérico tiene su importancia para todo lo que incluye proporción y porcentaje. El sistema numérico juega un papel crucial, tanto en nuestra vida cotidiana como en el mundo tecnológico. Con sus innumerables cualidades, nos simplifica mucho la vida, de lo que se ha hablado a continuación:
- Permite llevar la cuenta de todas las cosas que rodean a las personas. Como cuántas manzanas hay en la canasta, o la cantidad de cartones de leche que se comprarán, etc.
- Permite la representación única y precisa de diferentes tipos de números.
- Hacer una llamada telefónica es posible solo porque tenemos un sistema numérico adecuado y eficiente.
- Los ascensores utilizados en lugares públicos también dependen de sistemas numéricos para su funcionamiento.
- Cómputo de cualquier tipo de interés sobre las cantidades depositadas en bancos.
- Creación de contraseñas en ordenadores, con fines de seguridad.
- Cifrado de datos importantes, mediante la conversión de cifras a otro sistema numérico para evitar la piratería y el mal uso de los datos.
- Permite una fácil conversión de números con fines técnicos.
- La totalidad de la arquitectura informática depende de los sistemas numéricos (octal, hexadecimal). Cada fibra de datos se almacena en la computadora como un número.
Preguntas conceptuales
Pregunta 1: Convierta 128 10 en un número octal.
Solución:
En caso de conversión octal, tenemos que dividir los números por 8.
Operación Producción Resto 128/8 dieciséis 0 16/8 2 0 2/8 0 2 Por lo tanto, el número octal equivalente = 200 8
Pregunta 2: Convierte 128 10 a hexadecimal.
Solución:
En caso de conversión hexadecimal, dividimos los números por 16.
Operación Producción Resto 128/16 8 0 8/16 0 8 Por lo tanto, el número hexadecimal equivalente es 80 16
Pregunta 3: Convierta (1101) 2 en un número decimal.
Solución:
Ahora, multiplicando cada dígito de MSB a LSB con la reducción de la potencia del número base 2.
1 × 23 + 1 × 22 + 0 × 21 + 1 × 20
= 8 + 4 + 0 + 1
= 13
Por lo tanto, (1101) 2 = (13) 10
Pregunta 4: Convierta (214) 8 en un número binario.
Solución:
Sabemos,
2 → 010
1 → 001
4 → 100
Por lo tanto, (214) 8 = (010001100) 2
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA