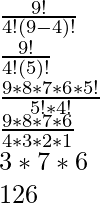Las permutaciones y combinaciones son una rama de las matemáticas que se ocupa del estudio de la selección de un subconjunto de elementos de la colección completa. En las combinaciones no importa el orden de selección de los artículos. Los elementos se pueden reorganizar en el formato deseado. Por ejemplo, hay tres alfabetos A, B y C. Si tenemos que seleccionar dos alfabetos, tenemos AB, BC y AC. Aquí, la selección de AB es equivalente a la selección de BA.
Sin embargo, en caso de que los números sean demasiado grandes, estos cálculos no se pueden realizar manualmente. Por lo tanto, tenemos,
norte C r =
donde n = total de elementos a recoger
r = los elementos a elegir
Por lo tanto, en el ejemplo estatal,
norte C r = 3 C 2
= 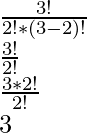
¿Cuántas strings de bits de longitud 9 tienen exactamente 4 0?
Solución:
Tenemos,
Número total de lugares para elegir = 9
El número de lugares para llenar con 0’s = 4
Por lo tanto, tenemos que llenar 4 lugares con 0 de un total de 9 lugares.
Según la fórmula de las combinaciones, donde no importa el orden de selección.
norte C r =
donde n = total de elementos a recoger
r = los elementos a elegir
Al sustituir los valores que obtenemos,
=
Por lo tanto,
Hay 126 formas de tener strings de 9 bits que contengan exactamente 4 0.
Preguntas similares
Pregunta 1. Averigüe de cuántas maneras se puede elegir un equipo de proyecto de 7 hombres y 10 mujeres de la oficina de 9 hombres y 12 mujeres.
Solución:
Aquí tenemos que encontrar de cuántas maneras se puede seleccionar un equipo de proyecto en una oficina.
De este modo,
Para elegir 7 hombres de 9 hombres
⇒ 9 C 5 vías = 9!/(9-5)!5!
⇒ 9!/4!5!
⇒ 9 × 8 × 7 × 6 × 5!/4 × 3 × 2 × 1 × 5!
⇒ 3024/24
= 126
Más lejos,
Para elegir 10 mujeres de 12 mujeres
⇒ 12 C 10 = 12!/(12 – 10)!10!
⇒ 12 × 11 × 10!/2!10!
⇒ 132/2
⇒ 66
Por lo tanto
El equipo del proyecto puede ser elegido en el
⇒ 66 × 126 vías
⇒ 8316 formas
Pregunta 2. Averigüe C(25, 23). C(n, r) = n!/(n – r)!r!
Solución:
Aquí tenemos,
norte = 25
r = 23
Sustituyendo los valores de n y r en C(n, r) = n!/(n – r)!r!
⇒ C(25, 23) = 25!/(25 – 23)!23!
⇒ C(25, 23) = 25!/(2)!23!
⇒ C(25, 23) = 25 × 24 × 23!/2! × 23!
⇒ C(25, 23) = 25 × 24/ 2
⇒ C(25, 23) = 600/2
⇒ C(25, 23) = 300
Por lo tanto,
⇒ C(25, 23). C(n,r)=n!/(n – r)!r! = 300
Pregunta 3. Averigüe de cuántas maneras se pueden seleccionar las luces de un candelabro que tiene 6 luces pequeñas y 8 luces grandes, entre 8 luces pequeñas y 10 luces grandes.
Solución:
Aquí tenemos que seleccionar luces para el candelabro.
Primero encontrando la selección para luces pequeñas
Seleccionando, 6 lucecitas de 8 lucecitas
⇒ 8 C 6 = 8!/(8-6)!6!
⇒ 8!/2!6!
⇒ ¡8 × 7 × 6!/2 × 1 × 6!
Resolviendo
⇒ 56/2
⇒ 28
⇒ 8 C 6 = 28
Por lo tanto,
Las luces pequeñas se pueden seleccionar de 28 maneras
Selección adicional de luces grandes
Seleccionando, 8 luces grandes de 10 luces grandes
⇒ 10 C 8 = 10!/(10 – 8)!8!
⇒ 10!/2!8!
⇒ 10 × 9 × 8!/2 × 1 × 8!
Resolviendo
⇒ 90/2
⇒ 45
10 C 8 = 45
De este modo,
Las luces grandes se pueden seleccionar de 45 maneras
Por lo tanto,
Las luces pequeñas y grandes en un candelabro se pueden seleccionar en
⇒ 28 × 45
⇒ 1260 formas
Pregunta 4. Averigüe C(15, 13). C(n, r) = n!/(n – r)!r!
Solución:
Aquí tenemos,
n = 15
r = 13
Sustituyendo los valores de n y r en C(n, r) = n!/(n – r)!r!
⇒ C(15, 13) = 15!/(15 – 13)!13!
⇒ C(15, 13) = 15!/(2)!13!
⇒ C(15, 13) = 15 × 14 × 13!/2! × 13!
⇒ C(15, 13) = 15 × 14/2
⇒ C(15, 13) = 210/2
⇒ C(15, 13) = 105
Por lo tanto,
⇒ C(15, 13). C(n,r)=n!/(n – r)!r! = 105
Pregunta 5. Averigüe C(50, 47). C(n, r) = n!/(n – r)!r!
Solución:
Aquí tenemos,
norte = 50
r = 47
Sustituyendo los valores de n y r en C(n, r) = n!/(n – r)!r!
⇒ C(50, 47) = 50!/(50 – 47)!47!
⇒ C(50, 47) = 50!/(3)!47!
⇒ C(50, 47) = 50 × 49 × 48 × 47!/3! × 47!
⇒ C(50, 47) = 50 × 49 × 48/3 × 2
⇒ C(50, 47) = 117600/6
⇒ C(50, 47) = 19600
Por lo tanto,
⇒ C(50, 47). C(n,r)=n!/(n – r)!r! = 19600
Publicación traducida automáticamente
Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA