Cuenta de cuadrados perfectos de longitud dada

Dado un número entero N , la tarea es encontrar el número de cuadrados perfectos de longitud N.
Ejemplos:

Entrada: N = 1
Salida: 3
Explicación: Los cuadrados perfectos de un dígito son 1, 4 y 9.
Entrada: N = 2
Salida: 6
Explicación: Los cuadrados perfectos de dos dígitos son 16, 25, 36, 49, 64 y 81 .

Enfoque ingenuo: para resolver este problema, podemos verificar todos los números entre 10 ^{(N – 1)} y 10 ^N – 1 e incrementar el contador cada vez que encontramos un cuadrado perfecto.
A continuación se muestra la implementación del enfoque anterior:

C++

// C++ Program to count perfect
// squares of given length
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to check if a
// number is perfect square
bool isPerfectSquare(long double x)
{
    // Find floating point value of
    // square root of x.
    long double sr = sqrt(x);
 
    // If square root is an integer
    return ((sr - floor(sr)) == 0);
}
 
// Function to return the count of
// n digit perfect squares
int countSquares(int n)
{
    // Initialize result
    int cnt = 0;
 
    // Traverse through all numbers
    // of n digits
    for (int i = pow(10, (n - 1));
         i < pow(10, n); i++) {
 
        // Check if current number
        // 'i' is perfect square
        if (i != 0 && isPerfectSquare(i))
            cnt++;
    }
    return cnt;
}
 
// Driver code
int main()
{
    int n = 3;
    cout << countSquares(n);
    return 0;
}

Java

// Java Program to count perfect
// squares of given length
class GFG{
 
// Function to check if a
// number is perfect square
static boolean isPerfectSquare(double x)
{
     
    // Find floating point value of
    // square root of x.
    double sr = Math.sqrt(x);
 
    // If square root is an integer
    return ((sr - Math.floor(sr)) == 0);
}
 
// Function to return the count of
// n digit perfect squares
static int countSquares(int n)
{
     
    // Initialize result
    int cnt = 0;
 
    // Traverse through all numbers
    // of n digits
    for(int i = (int) Math.pow(10, (n - 1));
                  i < Math.pow(10, n); i++)
    {
 
        // Check if current number
        // 'i' is perfect square
        if (i != 0 && isPerfectSquare(i))
            cnt++;
    }
    return cnt;
}
 
// Driver code
public static void main(String[] args)
{
    int n = 3;
    System.out.print(countSquares(n));
}
}
 
// This code is contributed by Rajput-Ji

Python3

# Python3 Program to count perfect
# squares of given length
import math;
 
# Function to check if a
# number is perfect square
def isPerfectSquare(x):
 
    # Find floating point value of
    # square root of x.
    sr = math.sqrt(x);
 
    # If square root is an integer
    return ((sr - math.floor(sr)) == 0);
 
# Function to return the count of
# n digit perfect squares
def countSquares(n):
 
    # Initialize result
    cnt = 0;
 
    # Traverse through all numbers
    # of n digits
    for i in range(int(math.pow(10, (n - 1))),
                   int(math.pow(10, n))):
 
        # Check if current number
        # 'i' is perfect square
        if (i != 0 and isPerfectSquare(i)):
            cnt += 1;
     
    return cnt;
 
# Driver code
n = 3;
print(countSquares(n));
 
# This code is contributed by Akanksha_Rai

C#

// C# program to count perfect
// squares of given length
using System;
 
class GFG{
 
// Function to check if a
// number is perfect square
static bool isPerfectSquare(double x)
{
     
    // Find floating point value of
    // square root of x.
    double sr = Math.Sqrt(x);
 
    // If square root is an integer
    return ((sr - Math.Floor(sr)) == 0);
}
 
// Function to return the count of
// n digit perfect squares
static int countSquares(int n)
{
     
    // Initialize result
    int cnt = 0;
 
    // Traverse through all numbers
    // of n digits
    for(int i = (int) Math.Pow(10, (n - 1));
                  i < Math.Pow(10, n); i++)
    {
 
       // Check if current number
       // 'i' is perfect square
       if (i != 0 && isPerfectSquare(i))
           cnt++;
    }
    return cnt;
}
 
// Driver code
public static void Main(String[] args)
{
    int n = 3;
     
    Console.Write(countSquares(n));
}
}
 
// This code is contributed by sapnasingh4991

Javascript

<script>
// Javascript Program to count perfect
// squares of given length
 
// Function to check if a
// number is perfect square
function isPerfectSquare(x)
{
    // Find floating point value of
    // square root of x.
    let sr = Math.sqrt(x);
 
    // If square root is an integer
    return ((sr - Math.floor(sr)) == 0);
}
 
// Function to return the count of
// n digit perfect squares
function countSquares(n)
{
    // Initialize result
    let cnt = 0;
 
    // Traverse through all numbers
    // of n digits
    for (let i = Math.pow(10, (n - 1));
         i < Math.pow(10, n); i++) {
 
        // Check if current number
        // 'i' is perfect square
        if (i != 0 && isPerfectSquare(i))
            cnt++;
    }
    return cnt;
}
 
// Driver code
let n = 3;
document.write(countSquares(n));
 
// This code is contributed by subhammahato348.
</script>

Producción:

Enfoque eficiente: para resolver este problema, simplemente podemos encontrar el número de cuadrados perfectos de longitud N usando una fórmula:

Un número n tiene d dígitos si ${10}^{d-1}\le n< {10}^{d}$
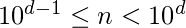
Por lo tanto, un cuadrado perfecto n ² tiene d dígitos si 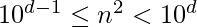${10}^{d-1}\le {n}^{2}< {10}^{d}$ o $\sqrt{10}^{d-1}\le n<\sqrt{10}^d.$
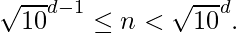
Por lo tanto, la respuesta requerida para el conteo de cuadrados perfectos de N dígitos es $\left\lceil\sqrt{10^N}\right\rceil-\left\lceil\sqrt{10^{N-1}}\right\rceil$

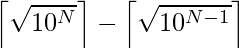
A continuación se muestra la implementación del enfoque anterior:

C++

// C++ Program to count
// perfect squares of given length
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to return the count of
// n digit perfect squares
int countSquares(int n)
{
    int r = ceil(sqrt(pow(10, n)));
    int l = ceil(sqrt(pow(10, n - 1)));
    return r - l;
}
 
// Driver code
int main()
{
    int n = 3;
    cout << countSquares(n);
    return 0;
}

Java

// Java Program to count perfect
// squares of given length
class GFG{
 
// Function to return the count
// of n digit perfect squares
static int countSquares(int n)
{
    int r = (int) Math.ceil(Math.sqrt
                           (Math.pow(10, n)));
    int l = (int) Math.ceil(Math.sqrt
                           (Math.pow(10, n - 1)));
    return r - l;
}
 
// Driver code
public static void main(String[] args)
{
    int n = 3;
    System.out.print(countSquares(n));
}
}
 
// This code is contributed by Rohit_ranjan

Python3

# Python3 program to count perfect 
# squares of given length
import math
 
# Function to return the count
# of n digit perfect squares
def countSquares(n):
 
    r = math.ceil(math.sqrt
                 (math.pow(10, n)));
    l = math.ceil(math.sqrt
                 (math.pow(10, n - 1)));
     
    return r - l;
     
# Driver code
n = 3;
print(countSquares(n));
 
# This code is contributed by grand_master

C#

// C# Program to count perfect
// squares of given length
using System;
class GFG{
 
// Function to return the count
// of n digit perfect squares
static int countSquares(int n)
{
    int r = (int) Math.Ceiling(Math.Sqrt
                              (Math.Pow(10, n)));
    int l = (int) Math.Ceiling(Math.Sqrt
                              (Math.Pow(10, n - 1)));
    return r - l;
}
 
// Driver code
public static void Main()
{
    int n = 3;
    Console.Write(countSquares(n));
}
}
 
// This code is contributed by Nidhi_Biet

Javascript

<script>
 
// JavaScript Program to count
// perfect squares of given length
 
// Function to return the count of
// n digit perfect squares
function countSquares(n)
{
    let r = Math.ceil(Math.sqrt(Math.pow(10, n)));
    let l = Math.ceil(Math.sqrt(Math.pow(10, n - 1)));
    return r - l;
}
 
// Driver code
let n = 3;
document.write(countSquares(n));
 
</script>

Producción:

Complejidad de tiempo: O(N)

Espacio Auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por spp____ y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta