Recuento de números enteros en un rango que tiene un número par de dígitos impares y un número impar de dígitos pares

Dado un rango [L, R] , la tarea es contar los números que tienen un número par de dígitos impares y un número impar de dígitos pares. Por ejemplo, 

1. 8 tiene 1 dígito par y 0 dígitos impares: cumple la condición ya que 1 es impar y 0 es par.
2. 545 tiene 1 dígito par y 2 dígitos impares: cumple la condición ya que 1 es impar y 2 es par.
3. 4834 tiene 3 dígitos pares y 1 dígito impar: no cumple la condición ya que hay números impares (es decir, 1) de dígitos impares.

Ejemplos: 

Entrada: L = 1, R = 9 
Salida: 4 
2, 4, 6 y 8 son los únicos números enteros del 
rango dado que satisfacen las condiciones dadas.

Entrada: L = 1, R = 19 
Salida: 4 

Entrada: L = 123, R = 984 
Salida: 431 

Acercarse:  

• Caso 1 
  Hay un patrón en el que estos números aparecen entre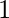  y 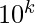 (donde 1<=k<=18). 
  Número de ocurrencias de 
  • 1 – 10 y 1 – 100 son 4
  • 1 – 1000 y 1 – 10000 son 454
  • 1 – 10000 y 1 – 100000 son 45454
• Caso 2 
  • Si el número de dígitos en un número es par, entonces no puede satisfacer la condición dada porque necesitamos un número impar (de dígitos) y un número par (de dígitos) para satisfacer nuestra condición y número impar + número par siempre es impar
  • Entonces, si el número de dígitos para un número dado (digamos n) es par, entonces su número de ocurrencias desde 1 es igual al número de ocurrencias desde 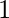 el más grande  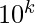(1<=k<=18) que es menor que n

Ejemplo: 
Sea n = 19, el número de dígitos en 19 es 2 
Por lo tanto, el número de ocurrencias de 1 a 19 = número de ocurrencias de 1 a 10 (ya que 10 es el más grande  menor que 19) 
 

• Caso 3 
  Si el número de dígitos para un número dado (por ejemplo, n) es impar, entonces el número de ocurrencias entre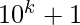  y n es igual a

donde  es el mayor  menor que n.

Implementación: ahora sabemos cómo calcular el número de ocurrencias de 1 a n dado. Por lo tanto, 
Número de ocurrencias de L a R = Número de ocurrencias hasta (R) – Número de ocurrencias hasta (L – 1) donde L no es igual a 1.

A continuación se muestra la implementación del enfoque anterior:  

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
#define ll long long
 
// Pattern table from Case 1
map<ll, ll> values{{1, 0},
                   {10, 4},
                   {100, 4},
                   {1000, 454},
                   {10000, 454},
                   {100000, 45454},
                   {1000000, 45454},
                   {10000000, 4545454},
                   {100000000, 4545454},
                   {1000000000, 454545454},
                   {10000000000, 454545454},
                   {100000000000, 45454545454},
                   {1000000000000, 45454545454},
                   {10000000000000, 4545454545454},
                   {100000000000000, 4545454545454},
                   {1000000000000000, 454545454545454},
                   {10000000000000000, 454545454545454},
                   {100000000000000000, 45454545454545454},
                   {1000000000000000000, 45454545454545454}};
 
// Function that returns the number of
// even and odd digits in val
pair<ll, ll> count_even_odd(ll val)
{
    ll even = 0, odd = 0;
    while (val)
    {
        ll num = val % 10;
        if (num % 2 == 0)
            even++;
        else
            odd++;
        val /= 10;
    }
    return make_pair(even, odd);
}
 
// Function that returns True if num
// satisfies the given condition
bool satisfies_condition(ll num)
{
    pair<ll, ll> answer = count_even_odd(num);
    ll even = answer.first;
    ll odd = answer.second;
 
    if (even % 2 == 1 and
         odd % 2 == 0) return true;
    return false;
}
 
// Function to return the count of
// numbers from 1 to val that
// satisfies the given condition
ll count_upto(ll val)
{
    // If the value is already present
    // in the values dict
    if (values.find(val) != values.end())
        return values[val];
 
    ll index = 1;
    for (int i = 0;
             i < to_string(val).length() - 1;
             i++)
         index *= 10;
 
    // If the value is even
    // Case 2
    if (to_string(val).length() % 2 == 0)
        return values[index];
 
    ll val_len = to_string(val).length();
    ll cnt = values[index];
 
    // Now the problem is to count the desired
    // numbers from 10**(val_len-1) + 1 to val
    ll left_end = index + 1;
 
    // Case 3
    // Eliminating all the even numbers
    cnt += (val - left_end) / 2;
    if (satisfies_condition(val) or
        satisfies_condition(left_end))
        cnt++;
 
    return cnt;
}
 
// Driver Code
int main()
{
    // Input l and r
    ll l = 123, r = 984;
    ll right = count_upto(r);
    ll left = 0;
 
    if (l == '1')
        left = 0;
    else
        left = count_upto(l - 1);
 
    cout << right - left << endl;
    return 0;
}
 
// This code is contributed by
// sanjeev2552

// Java implementation of the approach
import java.io.*;
import java.lang.*;
import java.util.*;
 
class GFG{
 
// Pattern table from Case 1
static HashMap<Long, Long> values = new HashMap<>();
 
public static void intitializeMap()
{
    values = new HashMap<>();
    values.put(1L, 0L);
    values.put(10L, 4L);
    values.put(100L, 4L);
    values.put(1000L, 454L);
    values.put(10000L, 454L);
    values.put(100000L, 45454L);
    values.put(1000000L, 45454L);
    values.put(10000000L, 4545454L);
    values.put(100000000L, 4545454L);
    values.put(1000000000L, 454545454L);
    values.put(10000000000L, 454545454L);
    values.put(100000000000L, 45454545454L);
    values.put(1000000000000L, 45454545454L);
    values.put(10000000000000L, 4545454545454L);
    values.put(100000000000000L, 4545454545454L);
    values.put(1000000000000000L, 454545454545454L);
    values.put(10000000000000000L, 454545454545454L);
    values.put(100000000000000000L, 45454545454545454L);
    values.put(1000000000000000000L, 45454545454545454L);
}
 
// Function that returns the number of
// even and odd digits in val
static long[] count_even_odd(long val)
{
    long even = 0, odd = 0;
    while (val > 0)
    {
        long num = val % 10;
        if (num % 2 == 0)
            even++;
        else
            odd++;
             
        val /= 10;
    }
    return (new long[] { even, odd });
}
 
// Function that returns True if num
// satisfies the given condition
static boolean satisfies_condition(long num)
{
    long[] answer = count_even_odd(num);
    long even = answer[0];
    long odd = answer[1];
 
    if (even % 2 == 1 && odd % 2 == 0)
        return true;
         
    return false;
}
 
// Function to return the count of
// numbers from 1 to val that
// satisfies the given condition
static long count_upto(long val)
{
     
    // If the value is already present
    // in the values dict
    if (values.containsKey(val))
        return values.get(val);
 
    long index = 1;
    for(int i = 0;
            i < Long.toString(val).length() - 1;
            i++)
        index *= 10;
 
    // If the value is even
    // Case 2
    if (Long.toString(val).length() % 2 == 0)
        return values.get(index);
 
    long val_len = Long.toString(val).length();
    long cnt = values.get(index);
 
    // Now the problem is to count the desired
    // numbers from 10**(val_len-1) + 1 to val
    long left_end = index + 1;
 
    // Case 3
    // Eliminating all the even numbers
    cnt += (val - left_end) / 2;
    if (satisfies_condition(val) ||
        satisfies_condition(left_end))
        cnt++;
 
    return cnt;
}
 
// Driver Code
public static void main(String[] args)
{
     
    // Input l and r
    long l = 123, r = 984;
 
    // Function to initialize the Map
    intitializeMap();
 
    long right = count_upto(r);
    long left = 0;
 
    if (l == '1')
        left = 0;
    else
        left = count_upto(l - 1);
 
    System.out.println(right - left);
}
}
 
// This code is contributed by Kingash

# Python3 implementation of the approach
 
# Pattern table from Case 1
values = {
    1: 0,
    10: 4,
    100: 4,
    1000: 454,
    10000: 454,
    100000: 45454,
    1000000: 45454,
    10000000: 4545454,
    100000000: 4545454,
    1000000000: 454545454,
    10000000000: 454545454,
    100000000000: 45454545454,
    1000000000000: 45454545454,
    10000000000000: 4545454545454,
    100000000000000: 4545454545454,
    1000000000000000: 454545454545454,
    10000000000000000: 454545454545454,
    100000000000000000: 45454545454545454,
    1000000000000000000: 45454545454545454,
}
 
# Function that returns the number of
# even and odd digits in val
def count_even_odd(val):
    even = odd = 0
    while val > 0:
        num = val % 10
        if num % 2 == 0:
            even += 1
        else:
            odd += 1
        val //= 10
 
    return even, odd
 
# Function that returns True if num
# satisfies the given condition
def satisfies_condition(num):
    even, odd = count_even_odd(num)
    if even % 2 == 1 and odd % 2 == 0:
        return True
    return False
 
 
# Function to return the count of numbers
# from 1 to val that satisfies the given condition
def count_upto(val):
 
    # If the value is already present in the
    # values dict
    if int(val) in values:
        return values[int(val)]
 
    # If the value is even
    # Case 2
    if len(val) % 2 == 0:
        return values[int('1' + '0' * (len(val) - 1))]
 
    val_len = len(val)
    count = values[int('1' + '0' * (val_len - 1))]
 
    # Now the problem is to count the desired
    # numbers from 10**(val_len-1) + 1 to val
    left_end = int('1' + '0' * (val_len - 1)) + 1
 
    # Case 3
    # Eliminating all the even numbers
    count += (int(val) - left_end) // 2
 
    if satisfies_condition(int(val)) or satisfies_condition(left_end):
        count += 1
    return count
 
 
if __name__ == '__main__':
 
    # Input L and R ( as a string )
    l, r = '123', '984'
 
    right = count_upto(r)
 
    left = 0
    if(l == '1'):
        left = 0
    else:
        left = count_upto(str(int(l)-1))
 
    print(right - left)

// C# implementation of the approach
using System;
using System.Collections.Generic;
 
class GFG{
 
// Pattern table from Case 1
static Dictionary<long,
                  long> values = new Dictionary<long,
                                                long>();
 
public static void intitializeMap()
{
    values = new Dictionary<long, long>();
    values.Add(1L, 0L);
    values.Add(10L, 4L);
    values.Add(100L, 4L);
    values.Add(1000L, 454L);
    values.Add(10000L, 454L);
    values.Add(100000L, 45454L);
    values.Add(1000000L, 45454L);
    values.Add(10000000L, 4545454L);
    values.Add(100000000L, 4545454L);
    values.Add(1000000000L, 454545454L);
    values.Add(10000000000L, 454545454L);
    values.Add(100000000000L, 45454545454L);
    values.Add(1000000000000L, 45454545454L);
    values.Add(10000000000000L, 4545454545454L);
    values.Add(100000000000000L, 4545454545454L);
    values.Add(1000000000000000L, 454545454545454L);
    values.Add(10000000000000000L, 454545454545454L);
    values.Add(100000000000000000L, 45454545454545454L);
    values.Add(1000000000000000000L, 45454545454545454L);
}
 
// Function that returns the number of
// even and odd digits in val
static long[] count_even_odd(long val)
{
    long even = 0, odd = 0;
     
    while (val > 0)
    {
        long num = val % 10;
        if (num % 2 == 0)
            even++;
        else
            odd++;
             
        val /= 10;
    }
    return (new long[]{ even, odd });
}
 
// Function that returns True if num
// satisfies the given condition
static bool satisfies_condition(long num)
{
    long[] answer = count_even_odd(num);
    long even = answer[0];
    long odd = answer[1];
 
    if (even % 2 == 1 && odd % 2 == 0)
        return true;
         
    return false;
}
 
// Function to return the count of
// numbers from 1 to val that
// satisfies the given condition
static long count_upto(long val)
{
     
    // If the value is already present
    // in the values dict
    if (values.ContainsKey(val))
        return values[val];
 
    long index = 1;
    for(int i = 0;
            i < val.ToString().Length - 1;
            i++)
        index *= 10;
 
    // If the value is even
    // Case 2
    if (val.ToString().Length % 2 == 0)
        return values[index];
 
    long val_len = val.ToString().Length;
    long cnt = values[index];
 
    // Now the problem is to count the desired
    // numbers from 10**(val_len-1) + 1 to val
    long left_end = index + 1;
 
    // Case 3
    // Eliminating all the even numbers
    cnt += (val - left_end) / 2;
    if (satisfies_condition(val) ||
        satisfies_condition(left_end))
        cnt++;
 
    return cnt;
}
 
// Driver Code
public static void Main(String[] args)
{
     
    // Input l and r
    long l = 123, r = 984;
 
    // Function to initialize the Map
    intitializeMap();
 
    long right = count_upto(r);
    long left = 0;
 
    if (l == '1')
        left = 0;
    else
        left = count_upto(l - 1);
 
    Console.WriteLine(right - left);
}
}
 
// This code is contributed by umadevi9616

<script>
 
// JavaScript implementation of the approach
 
// Pattern table from Case 1
let values = new Map();
values.set(1, 0)
values.set(10, 4)
values.set(100, 4)
values.set(1000, 454)
values.set(10000, 454)
values.set(100000, 45454)
values.set(1000000, 45454)
values.set(10000000, 4545454)
values.set(100000000, 4545454)
values.set(1000000000, 454545454)
values.set(10000000000, 454545454)
values.set(100000000000, 45454545454)
values.set(1000000000000, 45454545454)
values.set(10000000000000, 4545454545454)
values.set(100000000000000, 4545454545454)
values.set(1000000000000000, 454545454545454)
values.set(10000000000000000, 454545454545454)
values.set(100000000000000000, 45454545454545454)
values.set(1000000000000000000, 45454545454545454)
 
// Function that returns the number of
// even and odd digits in val
function count_even_odd(val)
{
    let even = 0, odd = 0;
    while (val)
    {
        let num = val % 10;
        if (num % 2 == 0)
            even++;
        else
            odd++;
        val = Math.floor(val/10);
    }
    return [even, odd];
}
 
// Function that returns True if num
// satisfies the given condition
function satisfies_condition(num)
{
    let answer = count_even_odd(num);
    let even = answer[0];
    let odd = answer[1];
 
    if (even % 2 == 1 &&
        odd % 2 == 0) return true;
    return false;
}
 
// Function to return the count of
// numbers from 1 to val that
// satisfies the given condition
function count_upto(val)
{
 
    // If the value is already present
    // in the values dict
    if (values.has(val) == true)
        return values.get(val);
 
    let index = 1;
    for (let i = 0;i < val.toString().length - 1;i++)
        index *= 10;
 
    // If the value is even
    // Case 2
    if (val.toString().length % 2 == 0)
        return values.get(index);
 
    let val_len = Number.toString(val).length;
    let cnt = values.get(index);
 
    // Now the problem is to count the desired
    // numbers from 10**(val_len-1) + 1 to val
    let left_end = index + 1;
 
    // Case 3
    // Eliminating all the even numbers
    cnt += Math.floor((val - left_end) / 2);
    if (satisfies_condition(val) ||
        satisfies_condition(left_end))
        cnt++;
 
    return cnt;
}
 
// Driver Code
 
// Input l and r
let l = 123, r = 984;
let right = count_upto(r);
let left = 0;
 
if (l == '1')
    left = 0;
else
    left = count_upto(l - 1);
 
document.write(right - left);
 
// This code is contributed by shinjanpatra
 
</script>

431

Complejidad de tiempo: O(logn)
 Espacio auxiliar: O(19*2)