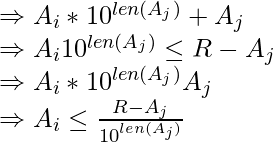Cuente el número en el rango dado generado al concatenar dos elementos de array

Dada una array arr[] de tamaño N y los números enteros L y R que definen el rango dado, la tarea es encontrar la cantidad de elementos en el rango dado que se pueden generar concatenando dos elementos cualesquiera de la array.

Ejemplos:

Entrada:   N = 2, L = 10, R = 52, arr = {2, 5}
Salida:   3
Explicación: Todos los pares disponibles  
(2, 2) => 22 (10 ≤ 22 ≤ 52)
(2, 5) = > 25 (10 ≤ 25 ≤ 52)
(5, 2) => 52 (10 ≤ 52 ≤ 52)
(5, 5) => 55 (10 ≤ 55 > 52) no válido
Por lo tanto, la salida es 3.

Entrada:   N = 3, L = 100, R = 1000, arr = {28, 5, 100}
Salida:   2
Explicación: Los únicos pares válidos disponibles  
(28, 5) => 285 (100 ≤ 285 ≤ 1000)
(5 , 28) => 528 (100 ≤ 528 ≤ 1000)
Resto otros pares se quedan cortos o más altos que el rango dado
Por lo tanto, la salida es 2.

Planteamiento: La idea para resolver el problema se basa en la siguiente observación:

Observaciones:

• La longitud del par válido es crucial ya que puede ayudarnos a distinguir los pares correctos.
• Si se permite la longitud, debemos verificar si cada elemento está en el límite o no.
• Similarmente  

Siga los pasos a continuación para implementar el enfoque anterior:

• Primero ordene la array dada.
• Encuentre la longitud del primer elemento del par.
• Para cualquier par {x, y} , x * 10 ^len(y) + y da el valor de “xy” cuando se concatenan.
• Luego, simplemente itera j de 1 a N : 
  • Use la condición anterior para encontrar el rango donde se encontrará el otro valor (por ejemplo, x ).
  • Use la búsqueda binaria para encontrar cuántos elementos de array posibles hay en el rango que puede asumir el valor x .
  • Incremente el conteo en esa cantidad.
• El conteo final es la respuesta requerida. 

A continuación se muestra la implementación del enfoque anterior:

// C++ code to implement the approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find valid pairs in given range
int ValidPair(int a[], int n, int l, int r)
{
    // Sort the array in the increasing order
    sort(a, a + n);
 
    // Precompute the powers
    // to avoid later calculations
    vector<int> pow10(17, 1);
    for (int i = 1; i <= 16; i++) {
        pow10[i] = pow10[i - 1] * 10;
    }
 
    int ans = 0;
    for (int j = 0; j < n; j++) {
 
        // Determining the length of a[j]
        int len = 0;
        int cur = a[j];
        while (cur) {
            cur /= 10;
            len++;
        }
 
        // Finding out the range
        int right = (r - a[j]) / pow10[len];
        int left = (l - a[j] + pow10[len] - 1) / pow10[len];
 
        // Applying the binary search to find number of
        // elements
        if (left <= right)
            ans += (upper_bound(a, a + n, right)
                    - lower_bound(a, a + n, left));
    }
    return ans;
}
 
// Driver Code
int main()
{
    int N = 2;
    int L = 10, R = 52;
    int arr[2] = { 2, 5 };
    cout << ValidPair(arr, N, L, R) << endl;
    return 0;
}

# Python3 code for the above approach
def upper_bound(arr, X) :
    low = 0
    high = len(arr)
     
    while low < high :
        mid = low + int((high - low) / 2)
         
        if (X >= arr[mid]) :
            low = mid + 1
        else :
            high = mid;
             
    if low < N and arr[low] <= X :
        low+=1
         
    return low
         
def lower_bound(a, val) :
     
    lo = 0
    hi = len(a) - 1
             
    while (lo < hi) :
         
        mid = (lo + int((hi - lo) / 2))
        if (a[mid] < val) :
            lo = mid + 1
        else :
            hi = mid
    return lo
     
# Function to find valid pairs in given range
def ValidPair(a, n, l, r) :
     
    # Sort the array in the increasing order
    a.sort()
     
    # Precompute the powers
    # to avoid later calculations
    #vector<int> pow10(17, 1);
    pow10 = [1]*17
     
    for i in range(1,17) :
        pow10[i] = pow10[i - 1] * 10
         
    ans = 0;
    for j in range(0,n) :
       
      # Determining the length of a[j]
      len = 0
      cur = a[j];
      while (cur>0) :
        cur = int(cur/10)
        len+=1
         
        # Finding out the range
        right = int((r - a[j]) / pow10[len])
        left = int((l - a[j] + pow10[len] - 1) / pow10[len])
         
        # Applying the binary search to find number of
        # elements
        if left <= right :
            ans += (upper_bound(a, right) - lower_bound(a, left))
    return ans
 
# Driver code
if __name__ == "__main__" :
     
    N = 2
    L = 10
    R = 52
    arr = [ 2, 5 ]
   
    # Function call
    print(ValidPair(arr, N, L, R))
 
# This code is contributed by adityapatil12

using System;
 
public class GFG{
 
  // Function to implement lower_bound
  public static int lower_bound(int[] arr, int N, int X)
  {
    int mid;
 
    // Initialise starting index and
    // ending index
    int low = 0;
    int high = N;
 
    // Till low is less than high
    while (low < high) {
      mid = low + (high - low) / 2;
 
      // If X is less than or equal
      // to arr[mid], then find in
      // left subarray
      if (X <= arr[mid]) {
        high = mid;
      }
 
      // If X is greater arr[mid]
      // then find in right subarray
      else {
        low = mid + 1;
      }
    }
 
    // if X is greater than arr[n-1]
    if(low < N && arr[low] < X) {
      low++;
    }
 
    // Return the lower_bound index
    return low;
  }
 
  // Function to implement upper_bound
  public static int upper_bound(int[] arr, int N, int X)
  {
    int mid;
 
    // Initialise starting index and
    // ending index
    int low = 0;
    int high = N;
 
    // Till low is less than high
    while (low < high) {
      // Find the middle index
      mid = low + (high - low) / 2;
 
      // If X is greater than or equal
      // to arr[mid] then find
      // in right subarray
      if (X >= arr[mid]) {
        low = mid + 1;
      }
 
      // If X is less than arr[mid]
      // then find in left subarray
      else {
        high = mid;
      }
    }
 
    // if X is greater than arr[n-1]
    if(low < N && arr[low] <= X) {
      low++;
    }
 
    // Return the upper_bound index
    return low;
  }
 
  // Function to find valid pairs in given range
  public static int ValidPair(int[] a, int n, int l, int r)
  {
    // Sort the array in the increasing order
    Array.Sort(a);
 
    // Precompute the powers
    // to avoid later calculations
    int[] pow10 = new int[17];
    for(int i=0;i<17;i++)
    {
      pow10[i]=1;
    }
    for (int i = 1; i <= 16; i++) {
      pow10[i] = pow10[i - 1] * 10;
    }
 
    int ans = 0;
    for (int j = 0; j < n; j++) {
 
      // Determining the length of a[j]
      int len = 0;
      int cur = a[j];
      while (cur>0) {
        cur /= 10;
        len++;
      }
 
      // Finding out the range
      int right = (r - a[j]) / pow10[len];
      int left = (l - a[j] + pow10[len] - 1) / pow10[len];
 
      // Applying the binary search to find number of
      // elements
      if (left <= right)
        ans += (upper_bound(a,a.Length, right)
                - lower_bound(a, a.Length, left));
    }
    return ans;
  }
 
  static public void Main (){
 
    int N = 2;
    int L = 10;
    int R = 52;
    int[] arr = { 2, 5 };
    Console.WriteLine( ValidPair(arr, N, L, R));
  }
}
 
// This code is contributed by akashish__

<script>
        // JavaScript code for the above approach
        function upper_bound(arr, N, X) {
            let mid;
            let low = 0;
            let high = arr.length;
 
            while (low < high) {
 
                mid = low + (high - low) / 2;
                if (X >= arr[mid]) {
                    low = mid + 1;
                }
 
                else {
                    high = mid;
                }
            }
 
            if (low < N && arr[low] <= X) {
                low++;
            }
 
            return low;
        }
        function lower_bound(a, val) {
            let lo = 0, hi = a.length - 1;
            while (lo < hi) {
                let mid = Math.floor(lo + (hi - lo) / 2);
                if (a[mid] < val)
                    lo = mid + 1;
                else
                    hi = mid;
            }
            return lo;
        }
 
        function ValidPair(a, n, l, r)
        {
            a.sort(function (a, b) { return a - b })
            let pow10 = new Array(17).fill(1);
            for (let i = 1; i <= 16; i++) {
                pow10[i] = pow10[i - 1] * 10;
            }
 
            let ans = 0;
            for (let j = 0; j < n; j++) {
 
                let len = 0;
                let cur = a[j];
                while (cur) {
                    cur = Math.floor(cur / 10);
                    len++;
                }
 
 
                let right = (r - a[j]) / pow10[len];
                let left = (l - a[j] + pow10[len] - 1) / pow10[len];
 
 
                if (left <= right)
                    ans += (upper_bound(a, a + n, right)
                        - lower_bound(a, a + n, left));
            }
            return ans;
        }
 
        let N = 2;
        let L = 10, R = 52;
        let arr = [2, 5];
        document.write(ValidPair(arr, N, L, R) + '<br>');
 
    // This code is contributed by Potta Lokesh
    </script>

3

Complejidad de tiempo: O(N * logN)
Espacio auxiliar: O(1)