Cuente los Nodes en el árbol dado cuyo peso es primo

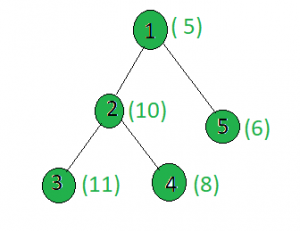
Dado un árbol y los pesos de todos los Nodes, la tarea es contar el número de Nodes cuyo peso es primo.
Ejemplos: 
 

Aporte: 
 

Salida: 2 
Solo los pesos de los Nodes 1 y 3 son primos. 
 

Enfoque: realice dfs en el árbol y para cada Node, verifique si su peso es principal o no.
A continuación se muestra la implementación del enfoque anterior:
 

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
int ans = 0;
 
vector<int> graph[100];
vector<int> weight(100);
 
// Function that returns true
// if n is prime
bool isprime(int n)
{
    for (int i = 2; i * i <= n; i++)
        if (n % i == 0)
            return false;
    return true;
}
 
// Function to perform dfs
void dfs(int node, int parent)
{
    // If weight of node is prime or not
    if (isprime(weight[node]))
        ans += 1;
 
    for (int to : graph[node]) {
        if (to == parent)
            continue;
        dfs(to, node);
    }
}
 
// Driver code
int main()
{
    // Weights of the node
    weight[1] = 5;
    weight[2] = 10;
    weight[3] = 11;
    weight[4] = 8;
    weight[5] = 6;
 
    // Edges of the tree
    graph[1].push_back(2);
    graph[2].push_back(3);
    graph[2].push_back(4);
    graph[1].push_back(5);
 
    dfs(1, 1);
 
    cout << ans;
 
    return 0;
}

// Java implementation of the approach
import java.util.*;
 
class GFG{
  
static int ans = 0;
 
static Vector<Integer>[] graph = new Vector[100];
static int[] weight = new int[100];
  
// Function that returns true
// if n is prime
static boolean isprime(int n)
{
    for (int i = 2; i * i <= n; i++)
        if (n % i == 0)
            return false;
    return true;
}
  
// Function to perform dfs
static void dfs(int node, int parent)
{
    // If weight of node is prime or not
    if (isprime(weight[node]))
        ans += 1;
  
    for (int to : graph[node]) {
        if (to == parent)
            continue;
        dfs(to, node);
    }
}
  
// Driver code
public static void main(String[] args)
{
    for (int i = 0; i < 100; i++)
        graph[i] = new Vector<>();
     
    // Weights of the node
    weight[1] = 5;
    weight[2] = 10;
    weight[3] = 11;
    weight[4] = 8;
    weight[5] = 6;
  
    // Edges of the tree
    graph[1].add(2);
    graph[2].add(3);
    graph[2].add(4);
    graph[1].add(5);
  
    dfs(1, 1);
  
    System.out.print(ans);
}
}
 
// This code is contributed by Rajput-Ji

# Python3 implementation of the approach
ans = 0
 
graph = [[] for i in range(100)]
weight = [0] * 100
 
# Function that returns true
# if n is prime
def isprime(n):
    i = 2
    while(i * i <= n):
        if (n % i == 0):
            return False
        i += 1
    return True
 
# Function to perform dfs
def dfs(node, parent):
    global ans
     
    # If weight of the current node is even
    if (isprime(weight[node])):
        ans += 1;
     
    for to in graph[node]:
        if (to == parent):
            continue
        dfs(to, node)
 
# Driver code
 
# Weights of the node
weight[1] = 5
weight[2] = 10
weight[3] = 11
weight[4] = 8
weight[5] = 6
 
# Edges of the tree
graph[1].append(2)
graph[2].append(3)
graph[2].append(4)
graph[1].append(5)
 
dfs(1, 1)
print(ans)
 
# This code is contributed by SHUBHAMSINGH10

// C# implementation of the approach
using System;
using System.Collections;
using System.Collections.Generic;
using System.Text;
 
class GFG{
     
static int ans = 0;
static ArrayList[] graph = new ArrayList[100];
static int[] weight = new int[100];
 
// Function that returns true
// if n is prime
static bool isprime(int n)
{
    for(int i = 2; i * i <= n; i++)
        if (n % i == 0)
            return false;
             
    return true;
}
 
// Function to perform dfs
static void dfs(int node, int parent)
{
     
    // If weight of node is prime or not
    if (isprime(weight[node]))
        ans += 1;
 
    foreach(int to in graph[node])
    {
        if (to == parent)
            continue;
             
        dfs(to, node);
    }
}
     
// Driver Code
public static void Main(string[] args)
{
    for(int i = 0; i < 100; i++)
        graph[i] = new ArrayList();
     
    // Weights of the node
    weight[1] = 5;
    weight[2] = 10;
    weight[3] = 11;
    weight[4] = 8;
    weight[5] = 6;
 
    // Edges of the tree
    graph[1].Add(2);
    graph[2].Add(3);
    graph[2].Add(4);
    graph[1].Add(5);
 
    dfs(1, 1);
 
    Console.Write(ans);
}
}
 
// This code is contributed by rutvik_56

<script>
 
// Javascript implementation of the approach
     
    let ans=0;
     
    let graph = new Array(100);
     
     
    let weight = new Array(100);
    for(let i=0;i<100;i++)
    {
        graph[i]=[];
        weight[i]=0;
    }
     
    // Function that returns true
    // if n is prime
    function isprime(n)
    {
        for (let i = 2; i * i <= n; i++)
            if (n % i == 0)
                return false;
        return true;
    }
     
    // Function to perform dfs
    function dfs(node,parent)
    {
         // If weight of node is prime or not
        if (isprime(weight[node]))
            ans += 1;
        for(let to=0;to<graph[node].length;to++)
        {
            if(graph[node][to] == parent)
                continue
            dfs(graph[node][to], node);  
        }
         
    }
     
    // Driver code
     
    x = 15;
   
    // Weights of the node
    weight[1] = 5;
    weight[2] = 10;
    weight[3] = 11;
    weight[4] = 8;
    weight[5] = 6;
       
   
    // Edges of the tree
    graph[1].push(2);
    graph[2].push(3);
    graph[2].push(4);
    graph[1].push(5);
     
     
    dfs(1, 1);
   
    document.write( ans);
     
    // This code is contributed by unknown2108
     
</script>

2

Análisis de Complejidad: 
 

• Complejidad de tiempo: O(N*sqrt(V)), donde V es el peso máximo de un Node en el árbol dado. 
  En DFS, cada Node del árbol se procesa una vez y, por lo tanto, la complejidad debida al DFS es O(N) cuando hay N Nodes en total en el árbol. Además, mientras se procesa cada Node, para comprobar si el valor del Node es primo o no, se ejecuta un ciclo hasta sqrt(V), donde V es el peso del Node. Por lo tanto, para cada Node, existe una complejidad adicional de O(sqrt(V)). Por lo tanto, la complejidad del tiempo es O(N*sqrt(V)).
• Espacio Auxiliar: O(1). 
  No se requiere ningún espacio adicional, por lo que la complejidad del espacio es constante.