Dado un número N en base decimal, encuentre el número de sus dígitos en cualquier base (base b)

Dado un número n en base 10, encuentre el número de dígitos en su representación en base b. 
Restricciones:  Ejemplos completos  :
 
 

Input : Number = 48 
        Base = 4
Output: 3
Explanation : (48)10 = (300)4

Input : Number = 1446
        Base = 7
Output: 4
Explanation : (446)10 = (4134)7

Un enfoque simple: convierta el número decimal en la base r dada y luego cuente el número de dígitos.
Un enfoque eficiente : Reside en la relación entre la base del número y el número de dígitos de ese número. 
Típicamente: Sea n un número entero positivo. La  representación base de  tiene  dígitos si  , que es el caso si  o  . Por lo tanto, el número de dígitos en la representación base b de n es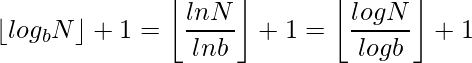 

En la ecuación anterior, se ha utilizado la propiedad logarítmica de cambio de base. Entonces calculamos el logaritmo del número en esa base que queremos calcular el número de dígitos. Y tome su valor mínimo y luego agregue 1. 
Esta idea se puede usar más para encontrar el número de dígitos de un número dado n de base b en base r. Todo lo que hay que hacer es convertir el número en base 10 y luego aplicar la fórmula anterior para encontrar dígitos. Sería más fácil calcular el logaritmo de cualquier base cuando el número está en base 10. 
 

// C++ program to Find Number of digits
// in base b.
#include <iostream>
#include <math.h>
using namespace std;
 
// function to print number of
// digits
void findNumberOfDigits(long n, int base)
{
    // Calculating log using base
    // changing property and then
    // taking it floor and then
    // adding 1.
    int dig = (int)(floor( log(n) /
                         log(base)) + 1);
     
    // printing output
    cout << "The Number of digits of "
         << "Number " << n << " in base "
         << base << " is " << dig;
}
 
// Driver method
int main()
{
    // taking inputs
    long n = 1446;
    int base = 7;
     
    // calling the method
    findNumberOfDigits(n, base);
    return 0;
}
 
// This code is contributed by Manish Shaw
// (manishshaw1)

// Java program to Find Number
// of digits in base b.
class GFG {
     
    // function to print number of digits
    static void findNumberOfDigits(long n, int base)
    {
         
        // Calculating log using base changing
        // property and then taking it
        // floor and then adding 1.
        int dig = (int)(Math.floor(
                        Math.log(n) / Math.log(base))
                        + 1);
         
         
        // printing output
        System.out.println("The Number of digits of Number "
                            + n + " in base " + base
                            + " is " + dig);
    }
 
    // Driver method   
    public static void main(String[] args)
    {
        // taking inputs
        long n = 1446;
        int base = 7;
         
        // calling the method
        findNumberOfDigits(n, base);
    }
}

# Python3 program to Find Number of digits
# in base b.
 
import math
 
# function to print number of
# digits
def findNumberOfDigits(n, base):
     
    # Calculating log using base
    # changing property and then
    # taking it floor and then
    # adding 1.
    dig = (math.floor(math.log(n) /
                 math.log(base)) + 1)
     
    # printing output
    print ("The Number of digits of"
      " Number {} in base {} is {}"
            . format(n, base, dig))
 
# Driver method
 
# taking inputs
n = 1446
base = 7
 
# calling the method
findNumberOfDigits(n, base)
 
# This code is contributed by
# Manish Shaw (manishshaw1)

// C# program to Find Number of digits
// in base b.
using System;
 
class GFG {
     
    // function to print number of
    // digits
    static void findNumberOfDigits(long n,
                                    int b)
    {
        // Calculating log using base
        // changing property and then
        // taking it floor and then
        // adding 1.
        int dig = (int)(Math.Floor(
          Math.Log(n) / Math.Log(b)) + 1);
         
        // printing output
        Console.Write("The Number of digits"
           + " of Number " + n + " in base "
                        + b + " is " + dig);
    }
 
    // Driver method
    public static void Main()
    {
        // taking inputs
        long n = 1446;
        int b = 7;
         
        // calling the method
        findNumberOfDigits(n, b);
    }
}
 
// This code is contributed by Manish Shaw
// (manishshaw1)

<?php
// PHP program to Find Number
// of digits in base b.
     
// function to print
// number of digits
function findNumberOfDigits($n, $b)
{
    // Calculating log using base
    // changing property and then
    // taking it floor and then
    // adding 1.
    $dig = (int)(floor(log($n) /
                       log($b)) + 1);
     
    // printing output
    echo ("The Number of digits".
               " of Number ". $n.
                  " in base ".$b.
                    " is ".$dig);
}
 
// Driver Code
$n = 1446;
$b = 7;
     
// calling the method
findNumberOfDigits($n, $b);
 
// This code is contributed by
// Manish Shaw (manishshaw1)
?>

<script>
 
// Javascript program to Find Number of digits
// in base b.
 
// function to print number of
// digits
function findNumberOfDigits(n, base)
{
    // Calculating log using base
    // changing property and then
    // taking it floor and then
    // adding 1.
    var dig = parseInt(Math.floor( Math.log(n) /
                        Math.log(base)) + 1);
     
    // printing output
    document.write("The Number of digits of "
        + "Number " + n + " in base "
        + base + " is " + dig);
}
 
// Driver method
 
// taking inputs
var n = 1446;
var base = 7;
 
// calling the method
findNumberOfDigits(n, base);
 
</script>

Producción : 
 

The Number of digits of Number 1446 in base 7 is 4

análisis de complejidad Complejidad de
 tiempo : O(logN)

Complejidad del espacio : O(1)