Aprendizaje profundo con PyTorch | Una introducción

PyTorch en muchos sentidos se comporta como las arrays que amamos de Numpy. Estas arrays Numpy, después de todo, son solo tensores. PyTorch toma estos tensores y simplifica su traslado a las GPU para obtener el procesamiento más rápido que se necesita cuando se entrenan redes neuronales. También proporciona un módulo que calcula automáticamente los gradientes (para retropropagación) y otro módulo específico para construir redes neuronales. En conjunto, PyTorch termina siendo más flexible con Python y la pila Numpy en comparación con TensorFlow y otros marcos.

Redes neuronales:
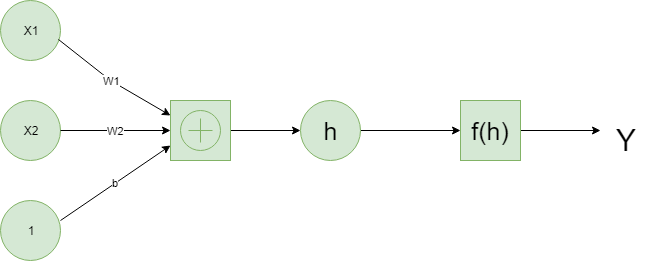
el aprendizaje profundo se basa en redes neuronales artificiales que existen de alguna forma desde finales de la década de 1950. Las redes se construyen a partir de partes individuales que se aproximan a las neuronas, normalmente llamadas unidades o simplemente «neuronas». Cada unidad tiene cierto número de entradas ponderadas. Estas entradas ponderadas se suman (una combinación lineal) y luego pasan a través de una función de activación para obtener la salida de la unidad.
A continuación se muestra un ejemplo de una red neuronal simple.

Tensores:
resulta que los cálculos de redes neuronales son solo un montón de operaciones de álgebra lineal en tensores, que son una generalización de arrays. Un vector es un tensor unidimensional, una array es un tensor bidimensional, una array con tres índices es un tensor tridimensional. La estructura de datos fundamental para las redes neuronales son tensores y PyTorch se basa en tensores.

Es hora de explorar cómo podemos usar PyTorch para construir una red neuronal simple.

# First, import PyTorch
import torch

Defina una función de activación (sigmoide) para calcular la salida lineal

def activation(x):
    """ Sigmoid activation function 
      
        Arguments
        ---------
        x: torch.Tensor
    """
    return 1/(1 + torch.exp(-x))

# Generate some data 
# Features are 3 random normal variables
features = torch.randn((1, 5))
  
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
  
# and a true bias term
bias = torch.randn((1, 1))

features = torch.randn((1, 5))crea un tensor con forma (1, 5), una fila y cinco columnas, que contiene valores distribuidos aleatoriamente según la distribución normal con media cero y desviación estándar uno.

weights = torch.randn_like(features)crea otro tensor con la misma forma que las características, que nuevamente contiene valores de una distribución normal.

Finalmente, bias = torch.randn((1, 1))crea un valor único a partir de una distribución normal.

Ahora calculamos la salida de la red usando la multiplicación de arrays.

y = activation(torch.mm(features, weights.view(5, 1)) + bias)

Así es como podemos calcular la salida de una sola neurona. El verdadero poder de este algoritmo ocurre cuando comienzas a apilar estas unidades individuales en capas y pilas de capas, en una red de neuronas. La salida de una capa de neuronas se convierte en la entrada de la siguiente capa. Con múltiples unidades de entrada y de salida, ahora necesitamos expresar los pesos como una array.

Definimos la estructura de la red neuronal e inicializamos los pesos y sesgos.

# Features are 3 random normal variables
features = torch.randn((1, 3))
  
# Define the size of each layer in our network
  
# Number of input units, must match number of input features
n_input = features.shape[1]     
n_hidden = 2                # Number of hidden units 
n_output = 1                # Number of output units
  
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
  
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
  
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))

Ahora podemos calcular la salida para esta red multicapa utilizando los pesos W1 y W2 y los sesgos B1 y B2.

h = activation(torch.mm(features, W1) + B1)
output = activation(torch.mm(h, W2) + B2)
print(output)