Demostrar que 1/(sen θ + cos θ) + 1/(sen θ – cos θ) = 2 sen θ/(1 – 2 cos2 θ)

La trigonometría es una rama de las matemáticas que generalmente se ocupa de los triángulos y los ángulos asociados con ella. La trigonometría ayuda a comprender las propiedades de los triángulos y la aplicación de las propiedades de los triángulos en la vida real. La trigonometría consta de dos palabras, a saber, trigon y geometría, que a su vez dice el significado en forma simple, es decir, geometría de triángulos (donde trigon se refiere a triángulos).

La trigonometría ayuda a comprender cómo encontrar los ángulos faltantes siempre que se proporcione la longitud de los lados de los triángulos, o también se puede usar para encontrar el valor de ciertos ángulos como 0,30,45,60,90, etc.

razones trigonométricas

Hay seis funciones o razones trigonométricas de un ángulo que están presentes en la trigonometría. Sus nombres y abreviaturas son seno (sin), coseno (cos), tangente (tan), cotangente (cot), secante (sec) y cosecante (csc). Una cosa importante a tener en cuenta aquí es que las fórmulas trigonométricas solo funcionan en el triángulo rectángulo. Veamos la siguiente imagen:

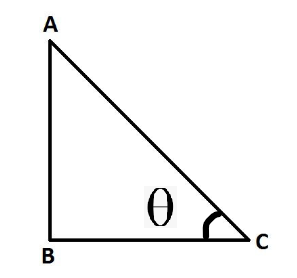
En este triángulo rectángulo, el lado AC se conoce como hipotenusa. El lado BC se conoce como la base del triángulo. El lado AB se conoce como la altura del triángulo. Desde el triángulo anterior, podemos enumerar fórmulas como arriba,

• sen∅ = AB/AC
• cos∅ = BC/AC
• tan∅ = AB/BC
• cuna∅ = BC/AB
• cosec∅ = AC/AB
• seg∅ = AC/BC

Fórmulas básicas de razones trigonométricas

• Tan ∅ = sen ∅/cos ∅
• sen ∅ = 1/coseg ∅
• cos ∅ = 1/seg ∅
• Tan ∅ = 1/cuna ∅
• sin(90° – x) = cos x
• cos(90° – x) = sen x
• tan(90° – x) = cuna x
• cuna(90° – x) = bronceado x
• cos ² x+sen ² x=1
• 1 + cuna ² θ = cosec ² θ
• 1 + bronceado ² θ = segundo ² θ

Demostrar que 1/(sen θ + cos θ) + 1/(sen θ – cos θ) = 2 sen θ/(1 – 2 cos ² θ)

Prueba:

Tomando la LHS de la ecuación,

1/(sen θ + cos θ) + 1/(sen θ – cos θ)

= (senθ – cos θ+sen θ + cos θ)/(sen ² θ – cos ² θ) [tomando mcm de las ecuaciones]

= 2senθ/(sen ² θ – cos ² θ)

en el RHS, el denominador está en términos de coseno. entonces, sustituyendo sen ² θ = 1 – cos ² θ de las fórmulas,

= 2senθ/(1- 2cos ² θ)

= lado derecho

Preguntas similares

Pregunta 1: Demuestre que (1 – cos ² θ) cosec ² θ = 1

Solución:

Tomando la LHS de la ecuación,

(1-cos ² θ)coseg ² θ

= (sen ² θ)coseg ² θ [como cos ² x + sen ² x = 1]

= cosec ² θ / cosec ² θ [como sen ² θ = 1/cosec ² θ]

= 1

= lado derecho

Pregunta 2: Demuestre que sec ² θ + tan ² θ = 2secθ – 1

Solución:

Tomando la LHS de la ecuación,

segundo ² θ + bronceado ² θ

= 1/cos ² θ + sen ² θ/cos ² θ [ como cos ∅ = 1/seg ∅ y Tan ∅ = sen ∅/cos ∅]

= (1+sen ² θ)/cos ² θ [tomando mcm]

= (1+1-cos ² θ )/cos ² θ [como cos ² x+sen ² x = 1]

= (2-cos ² θ )/cos ² θ  

= 2/cos ² θ – cos ² θ/cos ² θ [dividiendo el denominador]

= 2 seg ² θ -1

= lado derecho

Pregunta 3: Demostrar que cotθ + cosecθ = (cosθ + 1)/sinθ

Solución:

Tomando la LHS de la ecuación,

cotθ + cosecθ 

= cosθ/sinθ +1/sinθ [como sin ∅ = 1/coseg ∅ y cot∅ =cos∅ /sin∅ ]

= (cosθ+1)/sinθ [tomando mcm]

= lado derecho

Pregunta 4: Demuestre que tanθ.sinθ + secθ.cos ² θ = secθ 

Solución:

Tomando la LHS de la ecuación,

tanθ.sinθ + secθ.cos ² θ

= sinθ.sinθ/cosθ + cos ² θ/cosθ [como cos ∅ = 1/seg ∅ y Tan ∅ = sin ∅/cos ∅]

= (sen ² θ + cos ² θ)/cos θ [como cos ² x+sen ² x = 1]

= 1/cosθ

= segθ 

= lado derecho