El propio nombre de la trigonometría dice que es un tema que trata sobre la geometría de los triángulos y es muy útil para situaciones en las que se necesita saber cuándo hay algunos lados dados y necesitamos las relaciones entre los lados o los ángulos entre los lados. En trigonometría tenemos diferentes razones que son sen A, cos A, tan A, cot A, sec A, cosec A con la ayuda de las cuales se puede obtener la relación entre los lados y el ángulo entre los lados del triángulo.
Funciones trigonométricas
Las funciones trigonométricas definen la relación entre los lados y los ángulos y los ejemplos son sin A, cos A, tan A, cot A, sec A, cosec A. La relación entre diferentes funciones trigonométricas es una identidad trigonométrica . Las identidades son muy útiles para probar la desigualdad en las ecuaciones trigonométricas.
Los ejemplos son,
- Tan A= sen A/cos A
- sen A = 1/coseg A
- cos A= 1/seg A
- Tan A= 1/cuna A
Demostrar que 2 cos x – 2 cos 3 x = sen x sen 2x
Hay identidades básicas que se requieren para resolver el enunciado del problema anterior, veamos algunas de las identidades básicas de las 6 funciones trigonométricas que se requieren en este caso,
Requisitos previos Identidades utilizadas en la prueba
- sen 2x = 2 × sen x × cos x
- sen 2 x + cos 2 x = 1
- 1 – cos 2 x = sen 2 x
- sen x = 1/coseg x
- cos x – cos y =
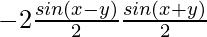
Ecuación trigonométrica dada
2 cos x – 2 cos 3 x= sen x sen 2x
LHS = 2 cos x – 2 cos 3 x
RHS = sen x sen 2x
Derivando prueba de LHS
Dado LHS
2 cos x – 2 cos 3 x
Paso 1
Tomando el 2 cos x que es común en ambos términos
= 2cos x (1-cos 2 x)
Paso 2
Sustituyendo 1-cos 2 x que es igual a sen 2 x
= 2 cos x (sen 2 x)
= (sen x) × (2 × senx × cos x)
Paso 3
Sustituyendo 2 × sen x × cos x que es sen 2x
= sen x × sen 2x
Del paso 3, se puede concluir que LHS = sin x × sin 2x que es igual a RHS y, por lo tanto,
sen x × sen 2x = sen x × sen 2x
LHS = RHS
Por lo tanto Probado.
Derivación de la prueba de la RHS
dado derecho
sen x sen 2x
Paso 1
Sustituyendo la fórmula de sen 2x en el RHS dado
= sen x × (2 senx cos x)
= 2 × sen 2 x × cosx
Paso 2
Sustituyendo la fórmula de sen 2 x que es igual a 1-cos 2 x
= 2 × (1-cos 2 x) × cos x
= 2 cos x – cos 3 x
Del paso 2 se puede concluir que RHS = 2cos x-cos 3 x que es igual a LHS y por lo tanto,
2cos x-cos 3 x = 2cos x-cos 3 x
LHS = RHS
Por lo tanto Probado.
Problemas de muestra
Pregunta 1: Resuelve la identidad trigonométrica: 4cos 2 x-4cos 4 x+cos 2 2x
Solución:
- Tomando 2cosx común en los dos primeros términos obtenemos
= 2cosx (2cosx-2cos 3x ) + cos 2 2x
- De la derivación anterior 2cosx – 2cos 3 x = senxsin2x
= 2cosx(senxsen2x) + cos 2 2x
- De la identidad estándar 2
= sen 2 2x + cos 2 2x
= 1
Pregunta 2: Resuelve la identidad trigonométrica: (1/ 8 × cosecx cosec2x cosx – 8 cosecx cosec2x cos 3 x)
Solución:
- Tomando los 4 cosecx cosec2x comunes en el denominador
= 1/4 cosecx cosec2x (2cosx -2cos 3 x)
- Usando la identidad 4
= (senx sen 2x)/4 × (2cosx -2cos 3 x)
- Por la identidad derivada la ecuación se convierte en
= (senx sen 2x) / (4 × senx sen2x)
= 1/4 = 0,25
Pregunta 3: Resuelve la identidad trigonométrica: (cos 3x – cosx) / (4cos 3 x – 4cosx)
Solución:
- Resolviendo el numerador usando la identidad 5
=
= -2senx sen 2x / 4cos 3 x – 4cosx
- Resolviendo el denominador multiplicando -1 y dividiendo por -1 para obtener el denominador de nuestra identidad derivada
= 2 sen x sen 2x/2(2cos 3 x-2cosx)
= sen x sen 2x/(2cos 3 x-2cosx)
= sen x sen 2x/ sen x sen 2x
= 1
Publicación traducida automáticamente
Artículo escrito por lokeshpotta20 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA