Demostrar que cos2θ (1+tan2θ) = 1

La trigonometría es la rama de las matemáticas que estudia las relaciones entre las proporciones de los lados de un triángulo rectángulo con sus ángulos. Aunque la trigonometría no tiene aplicaciones directas en la resolución de problemas reales, se aplica en una variedad de actividades. Por ejemplo, en la música, el sonido viaja en forma de ondas, y aunque este patrón no es tan regular como una función de seno o coseno, es beneficioso en el desarrollo de la música por computadora.

Funciones trigonométricas

Las funciones trigonométricas, también conocidas como funciones circulares, se definen como las funciones de un ángulo de un triángulo. Esto significa que estas funciones trigonométricas determinan la relación entre los ángulos y los lados de un triángulo. Seno, coseno, tangente, cotangente, secante y cosecante son las funciones trigonométricas básicas.

ecuación trigonométrica

Una ecuación que involucra una o más razones trigonométricas de ángulos desconocidos se conoce como ecuación trigonométrica. Se expresa como razones de ángulos seno (sin), coseno (cos), tangente (tan), cotangente (cot), secante (sec), cosecante (cosec). Por ejemplo, tan ² x – 3 = 0

Fórmulas de ecuaciones trigonométricas

Hay fórmulas básicas definidas para los 6 ángulos trigonométricos con respecto a los lados de un triángulo rectángulo. Si se conoce el ángulo adyacente al ángulo recto, la razón de los lados se puede encontrar fácilmente,

$\sin \theta = \frac{P}{B} \newline \cos \theta = \frac{B}{H} \newline \tan \theta = \frac{P}{B} \newline \cot \theta = \frac{B}{P} \newline \sec \theta = \frac{H}{B} \newline \cosec \theta = \frac{B}{P}$

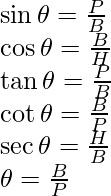
Donde P es la perpendicular, B es la base y H es la hipotenusa.

Identidades trigonométricas

Las identidades trigonométricas son ecuaciones que se relacionan con diferentes funciones trigonométricas y son verdaderas para cualquier valor de la variable que se encuentra en el dominio. A continuación se muestra la relación entre funciones trigonométricas, también conocidas como identidades trigonométricas recíprocas,

$\tan \theta= \frac{\sin \theta}{\cos \theta} \newline \cot \theta= \frac{1}{\tan \theta}=\frac{\cos \theta}{\sin \theta} \newline \sec \theta= \frac{1}{\cos \theta} \newline \cosec \theta= \frac{1}{\sin \theta}$

Identidades trigonométricas pitagóricas

sen ² θ + cos ² θ = 1
segundo ² θ – bronceado ² θ = 1
cosec ² θ – cuna ² θ = 1

Demuestre que cos ² θ (1 + tan ² θ) = 1.

Solución:

Para probar: cos ² θ (1 + tan ² θ) = 1.

Comenzando desde el lado izquierdo

=> cos ² θ (1 + tan ² θ) = 1.

$\sec^2 \theta = 1+\tan^2 \theta$

$=> \cos^2 \theta * (\sec^2 \theta)$

También, $\sec \theta=\frac{1}{\cos \theta}$

$=> cos^2 \theta * (\frac{1}{cos^2 \theta})$

$=> \frac{cos^2 \theta}{cos^2 \theta}=1 =$ lado derecho

A partir de aquí, se ve que el valor del lado izquierdo siempre será igual a 1. Por lo tanto, es independiente del valor de $\theta$ .

Ejemplos de preguntas

Pregunta 1: Demuestra que sen ² θ×(1+cot ² θ)=1

Solución:

Tomando el lado izquierdo

=> Sabemos que, $\cosec^2 \theta=1+cot^2 \theta$

=> $\sin^2 \theta * (\cosec^2 \theta)$

=> También, $\cosec \theta=\frac{1}{\sin \theta}$

=> $\sin^2 \theta * (\frac{1}{\sin^2 \theta})$ =1=lado derecho

Por lo tanto probado.

Pregunta 2: Demuestra que $\mathbf {tan^2 \theta * (cosec^2 \theta-1)=1}$

Solución:

Tomando el lado izquierdo

=> Sabemos que, $\cosec^2 \theta=1+\cot^2 \theta$

$=>\tan^2 \theta * (\cot^2 \theta)$

=> También, $\cot \theta=\frac{1}{\tan \theta}$

=> $\tan^2 \theta * (\frac{1}{\tan^2 \theta})$ =1=lado derecho

Por lo tanto probado.

Pregunta 3: Encuentra el valor de $\mathbf {sin^2 30\degree * (1+cot^2 30\degree)}$

Solución:

=> $sin^2 \theta * (1+cot^2 \theta)=1$ , independiente del valor del valor de $\theta$

Por lo tanto, el valor de $sin^2 30\degree * (1+cot^2 30\degree)$ es 1.

Pregunta 4: Demuestra que $\sec^2\theta*(1-\sin^2\theta)=1$

Solución:

=> $\sec^2\theta*(1-\sin^2\theta)$

=> Sabemos que, $\sin^2 \theta+\cos^2\theta=1$ , por lo tanto, $1-\sin^2 \theta=\cos^2\theta$

=> $\sec^2\theta*\cos^2\theta$

=> También, $\cos \theta=\frac{1}{\sec \theta}$

=> $\sec^2 \theta*\frac{1}{\sec^2 \theta}$ =1