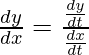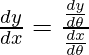Las derivadas de las funciones expresan la tasa de cambio en las funciones. Sabemos cómo calcular las derivadas de funciones estándar. La regla de la string, la regla del producto y la regla de la división se utilizan para calcular las derivadas de las funciones complejas que se componen de la composición de dos o más funciones. Estas funciones tienen dos variables que están relacionadas entre sí de manera implícita o explícita. A veces nos encontramos con funciones en las que las variables no están relacionadas entre sí implícita o explícitamente, sino que están relacionadas entre sí a través de una tercera variable. Veamos cómo calcular las derivadas de tales funciones en detalle.
¿Cómo encontrar derivadas de funciones en formas paramétricas?
Digamos que tenemos dos variables x e y, por lo general, dichas variables están relacionadas entre sí de manera implícita o explícita. Pero en algunos casos, estas variables se relacionan entre sí a través de una tercera variable. Esta forma se llama forma paramétrica de la ecuación y la variable se llama parámetro.
x = f(t) y y = g(t) aquí, t es un parámetro.
La derivada de tales funciones viene dada por la regla de la string,
![]() =
=![]()
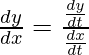 lo que sea
lo que sea![]()
Así, ![]() =
= ![]() (como
(como ![]() y
y ![]() )
)
Problemas de muestra
Pregunta 1: Halla ![]() , si x = acos(
, si x = acos( ![]() ) , y = asen(
) , y = asen( ![]() ).
).
Solución:
x = acos(θ) y y = asen(θ)
Ahora, averigüemos
⇒
⇒
⇒
Pregunta 2: Halla ![]() , si x = acos 2 (
, si x = acos 2 ( ![]() ) , y = asen 2 (
) , y = asen 2 ( ![]() ).
).
Solución:
x = acos 2 (
) , y = asen 2 (
)
Ahora, averigüemos
⇒
⇒
⇒
Pregunta 3: Encuentre ![]() , si x = en 2 + 2t, y = t en t = 0.
, si x = en 2 + 2t, y = t en t = 0.
Solución:
x = en 2 + 2t, y = t
Ahora, averigüemos
⇒
⇒
⇒
Pregunta 4: Encuentre ![]() , si x = en 3 + 2t 2 , y = t 2 en t = 1.
, si x = en 3 + 2t 2 , y = t 2 en t = 1.
Solución:
x = en 3 + 2t 2 , y = t 2
Ahora, averigüemos
⇒
⇒
Pregunta 5: Encuentra ![]() , si x = 4t, y =
, si x = 4t, y = ![]() en t = 1.
en t = 1.
Solución:
x = 4t, y =
Ahora, averigüemos
⇒
⇒
En t = 1
Pregunta 6: Encuentra ![]() , si x = 4e t , y = cos(t) en t = 1.
, si x = 4e t , y = cos(t) en t = 1.
Solución:
x = 4e t , y =cos(t)
Ahora, averigüemos
⇒
En t = 1
⇒
Pregunta 7: Encuentre![]() , si x = e t + sin(t), y = t 2 , at = 0.
, si x = e t + sin(t), y = t 2 , at = 0.
Solución:
x = e t + sen(t), y =t 2
Ahora, averigüemos
⇒
En t = 0
⇒
Pregunta 8: Encuentre ![]() , si x = tsin(t), y = cos(t), en t =
, si x = tsin(t), y = cos(t), en t = ![]() .
.
Solución:
x = tsen(t), y = cos(t)
Ahora, averigüemos
⇒
en t =
⇒
⇒
Pregunta 9: Encuentra ![]() , si x = 4t 2 + 10, y =t 2 en t = 1.
, si x = 4t 2 + 10, y =t 2 en t = 1.
Solución:
x = 4t 2 + 10, y = t 2
Ahora, averigüemos
⇒
⇒
En t = 1
Pregunta 10: Encuentre![]() , si x = en 2 , y = 2 en t = 1.
, si x = en 2 , y = 2 en t = 1.
Solución:
x = en 2 , y = 2 en
Ahora, averigüemos
⇒
⇒
En t = 1
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA