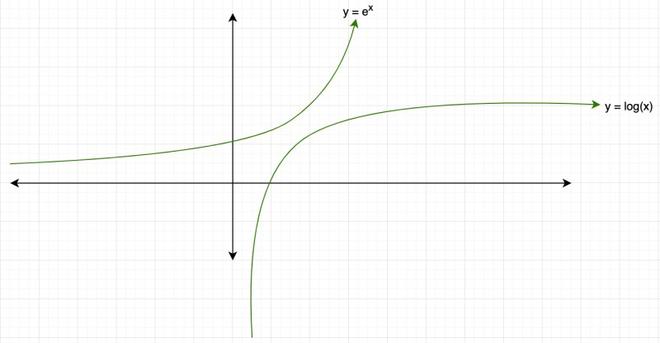
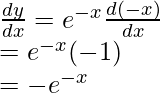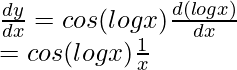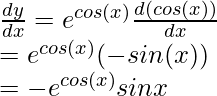Las funciones exponenciales y logarítmicas son una clase de funciones que se utilizan mucho en diferentes áreas de las ciencias. Las funciones exponenciales aumentan muy rápidamente y las funciones logarítmicas tienden a saturarse a medida que aumentan los valores de entrada. En la siguiente figura, se puede observar que a medida que aumenta la potencia de x, las funciones comienzan a crecer más rápido y la gráfica se vuelve más empinada. Las funciones exponenciales vienen en una clase similar de funciones.
La siguiente figura representa la gráfica de una función logarítmica y exponencial.
Derivada de la Función Exponencial
Comencemos mirando la función exponencial,
y = e x
Para su diferenciación, el uso de energía normal que se usa generalmente no funcionará. Entonces, obtengamos la derivada de esto usando límites. La derivada de una función usando límites viene dada por,

Ahora bien, este último límite ![]() es exactamente la definición de la derivada anterior f'(x) en x = 0, es decir, f'(0). Por lo tanto, la derivada se convierte en,
es exactamente la definición de la derivada anterior f'(x) en x = 0, es decir, f'(0). Por lo tanto, la derivada se convierte en,
f'(x) = segundo x f'(0) = segundo x
Entonces, en el caso de funciones exponenciales naturales, f(x) = e x
Nota: En casos exponenciales generales, por ejemplo, y = b x , donde b es un número real. La derivada para este tipo de función es
Pregunta 1: Diferenciar f(x) = 4e x – 5 x
Responder:
La derivación de e x seguirá siendo e x , la derivada de 5 x se convertirá en 5 x ln(5) como se explicó anteriormente.
Por lo tanto, f'(x) = 4e x – 5 x ln(x)
Pregunta 2: Diferenciar ![]()
Responder:
Aquí, siguiendo la regla del cociente, diferencie la función g(x):
Pregunta 3: Encuentra el valor de F'(x) en x=0 cuando f(x) = 7 x + 2e x
Responder:
Derivando: f'(x) = 7 x ln(7) + 2e x
en x=0, f'(0) = 7 0 ln(7) + 2e 0
= ln(7) + 2
= 3.945
Derivada de la función logarítmica
Ahora, veamos cómo se calculan las derivadas de la función logarítmica. Observe el hecho de que estas funciones son en realidad inversas entre sí.
Nota: Si dos funciones son inversas entre sí, entonces,
Es un hecho conocido que la exponencial natural y el logaritmo natural son inversas entre sí. Podemos usar la propiedad anterior para encontrar la derivada de la función logarítmica.
Digamos que f(x) = e x y g(x) = log e x.

Veamos algunos ejemplos de derivadas de ambas funciones,
Pregunta 1: Diferenciar: y(x) = x 5 – e x ln(x)
Responder:
Diferenciando usando la regla de la string:
Pregunta 2: Calcular las derivadas para
(i) e -x (ii) sen(logx) (iii) e cos(x)
Responder:
(i) Sea y = e -x , para encontrar la diferenciación de esta función necesitamos usar la regla de la string.
(ii) y = sen(logx). También requiere la regla de la string para la diferenciación.
(iii) y = e cos(x)
Pregunta 3: Calcula la derivada f(x) = 3e x + 10x 3 log(x).
Responder:
La derivada requiere la regla de la string y las fórmulas estudiadas anteriormente,
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
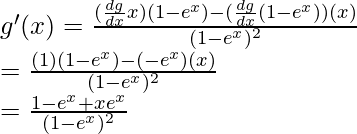
![Rendered by QuickLaTeX.com y'(x)= \frac{dy}{dx}x^5-[(\frac{dy}{dx}e^x)(ln(x))+(\frac{dy}{dx}ln(x))(e^x)]\\=5x^4-e^xln(x)-\frac{e^x}{x}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b01471f7f118daf2475401e20adf94f4_l3.png)