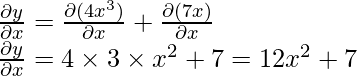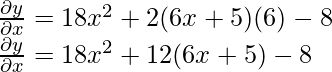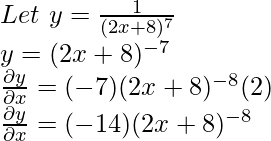Derivadas de funciones polinómicas

Las derivadas se utilizan en Cálculo para medir la tasa de cambio de una función con respecto a una variable. El uso de derivadas es muy importante en Matemáticas. Se utiliza para resolver muchos problemas matemáticos, como averiguar los máximos o mínimos de una función, la pendiente de una función, saber si una función es creciente o decreciente. Si una función se escribe como y = f(x) y queremos encontrar la derivada de esta función, entonces se escribirá como dy/dx y se puede pronunciar como la tasa de cambio de y con respecto a x.

La derivada de una función polinomial

Para calcular la derivada de una función polinomial, primero debes conocer la regla del producto de las derivadas y la regla básica de la derivada.

Regla del producto de la derivada

$\frac{\partial (x^{n})}{\partial x} = n\times x^{n-1}$

(Aquí n puede ser un valor positivo o negativo)

Entiéndase de esta manera: la antigua potencia de la variable se multiplica por el coeficiente de la variable y la nueva potencia de la variable se reduce en 1 a partir de la antigua potencia.

Ejemplo: encontrar la derivada de x ³ ?

Solución:

Sea y = x ³

$=> \frac{\partial y}{\partial x} = 3\times x^{3-1} = 3x^2$

Algunas reglas básicas de la derivada

Si y = cf(x)

$\frac{\partial y}{\partial x} = c\frac{\partial (f(x))}{\partial x}$

Si y = c

$\frac{\partial y}{\partial x} = 0$

$If \ y= f_{1}(x)\pm f_{1}(x)$

$\frac{\partial y}{\partial x} = \frac{\partial (f_{1}(x))}{\partial x}\pm \frac{\partial (f_{1}(x))}{\partial x}\\$

Ejemplo 1: ¿Encontrar la derivada de 4x ³ + 7x?

Solución:

Sea y = 4x ³ + 7x

$\frac{\partial y}{\partial x} = \frac{\partial (4x^{3})}{\partial x}+\frac{\partial (7x)}{\partial x} \\ \frac{\partial y}{\partial x} = 4\times 3\times x^{2} + 7 = 12x^2 + 7$