La derivada de una función f(x), es la tasa a la que cambia el valor de la función cuando cambia la entrada. En este contexto, x se denomina variable independiente y f(x) se denomina variable dependiente. Los derivados tienen aplicaciones en casi todos los aspectos de nuestras vidas. Desde los lanzamientos de cohetes hasta el diseño de nuestro tanque de agua, los profesionales utilizan derivados para medir la tasa de cambio y, a veces, analizar fenómenos físicos desde una perspectiva matemática. Calcular las derivadas de polinomios es bastante simple, las funciones trigonométricas y sus derivadas requieren atención adicional. Veamos cómo calcularlos en detalle.
Derivados
La definición formal y más básica de las derivadas implica límites. Geométricamente, para una función f(x), la derivada en el punto x representa la pendiente de una línea que es tangente a la curva en ese punto en particular. Usando esta intuición, se desarrolló la definición formal de las derivadas usando los límites. La siguiente figura muestra la intuición geométrica de las derivadas.

En esta figura, observe que la línea que une los puntos (x, f(x)) y (x, f(x + h)) es secante a la figura. Pero la suposición es que h se aproxima a cero. Entonces, de esta manera, a medida que el punto (x + h) se acerca más y más al punto x, la secante comienza lentamente a convertirse en una tangente. Por eso se dice que las derivadas no son más que la pendiente de las tangentes a la curva. Usando esta lógica, se da la primera definición de las derivadas.
Para una función f(x), en un punto x = a. La derivada se define como,
También se puede escribir como,
Esta es la definición de las derivadas. También denotamos las derivadas por ![]() o f'(x).
o f'(x).
Regla de la potencia de las derivadas
Esta es la regla más utilizada en derivados. Dice,
![]()
Esto se puede derivar a través de la definición de límite de las derivadas.
(x + h) n se puede abrir a través de la expansión binomial,
⇒
⇒
⇒
⇒
Pregunta 1: Encuentra la derivada de f(x) = √x.
Solución:
⇒
Esta es la forma indeterminada, usando la racionalización.
⇒
⇒
⇒
⇒
⇒
Derivadas de funciones trigonométricas
Primero se calculan las derivadas de la trigonométrica a través de la definición de límite. Antes de calcular estas derivadas y ver sus demostraciones, es necesario revisar algunas identidades de límite relacionadas con funciones trigonométricas.
y
Calculemos las derivadas de las tres funciones trigonométricas más importantes.
Demostrando la derivada de la función seno
![]()
Usando la definición antes mencionada de las derivadas
⇒
⇒
Usando las identidades límite descritas anteriormente,
⇒
Demostrando la derivada de la función coseno
![]()
Usando la definición antes mencionada de las derivadas
⇒
⇒
⇒
⇒
Usando las identidades límite descritas anteriormente,
⇒
Demostrando la derivada de la función tangente
![]()
Ahora que tenemos las derivadas de las funciones seno y coseno. Las derivadas de otras funciones se pueden calcular simplemente a través de las reglas del cociente y del producto.
La regla del cociente dice, para una función f(x) =
, la derivada de esta función está dada por,
En este caso tan(x) =
Así, h(x) = sin(x) y g(x) = cos(x).
⇒
⇒
⇒
Demostrando la derivada de la función secante
![]()
Esto se puede demostrar fácilmente a través de la regla de la string,
⇒
⇒
⇒
Demostrando la derivada de la función cosecante
![]()
Esto se puede demostrar fácilmente a través de la regla de la string,
⇒
⇒
⇒
Regla de prueba de producto
Hay diferentes formas de probar la regla del producto que incluye la definición de la derivación y la diferenciación logarítmica, veamos la última forma,
y= (f(x)g(x))’ = f'(x)g(x)+ f(x)g'(x)
Esto se puede probar fácilmente tomando el logaritmo natural,
ln y’= ln{(f(x)g(x))’} = lnf'(x) + lng'(x)
y’/y= f'(x)/f(x)+ g'(x)/g(x)
Por lo tanto, probado.
Veamos algunos problemas de muestra.
Problemas de muestra
Pregunta 1: Encuentra la derivada de la función f(x) en x = 0.
f(x) = sen 2 (x)
Solución:
Esta derivada es la combinación de la regla de la potencia y la regla de la string.
f'(x) =
⇒f'(x) =
Usando los resultados anteriores para la derivada de sin(x).
⇒f'(x) = 2sen(x)cos(x)
En x = 0
f'(x) = 0
Pregunta 2: Encuentra la derivada de la función f(x) en x = 0.
f(x) = 5seg(x) + 2cos(x)
Solución:
Esta derivada es simple.
f'(x) =
⇒f'(x) =
Usando los resultados anteriores para la derivada de sin(x).
⇒f'(x) = 5sec(x)tan(x) – 2sin(x).
en x = 0
f'(x) = 0
Pregunta 3: Encuentra la derivada de la función f(x) en x = 1.
f(x) = x2 + x4
Solución:
Esta derivada es una simple aplicación de la regla de la potencia.
f'(x) =
⇒f'(x) =
Usando los resultados anteriores para la derivada de sin(x).
⇒f'(x) = 2x + 4x 3
En x = 1
f'(x) = 6
Pregunta 4: Encuentra la derivada de la función f(x).
f(x) = ![]()
Solución:
Esta derivada es una simple aplicación de la regla del cociente.
La regla del cociente dice, para una función f(x) =
, la derivada de esta función está dada por,
Aquí h(x) = e x + 1 y g(x) = x
⇒
Pregunta 5: Usa la regla del Producto para diferenciar la función dada,
y = 5xsenx + 4x 2 cosx
Solución:
Diferenciar usando la regla del producto,
y’= 5senx + 5xcosx + 8xcosx – 4x 2 senx
y’= 5senx + 13xcosx – 4x 2 senx
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
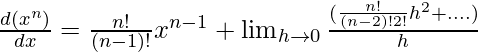
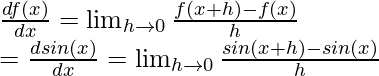
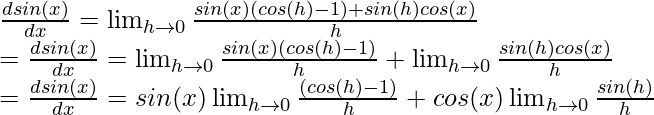
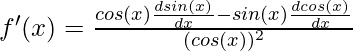
![Rendered by QuickLaTeX.com y'=y[\frac{f'(x)g(x)+ g'(x)f(x)}{f(x)g(x)}]\\ y'=f(x)g(x)[\frac{f'(x)g(x)+ g'(x)f(x)}{f(x)g(x)}]\\ y'= f'(x)g(x)+ g'(x)f(x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b1e3ef1c735f7ee4ae8578a135367b20_l3.png)