Derivados

Posted on by Rudeus Greyrat

Nos encontramos con muchas situaciones en la vida real en las que encontramos alguna variable para la que queremos saber su tasa de cambio. Por ejemplo, vemos un automóvil que circula por la carretera, nos interesa su posición y la velocidad a la que cambia su posición. La tasa de cambio de posición también se llama velocidad. En otro escenario de agua que fluye a través del tanque de agua, podríamos estar interesados ​​en medir la velocidad a la que el agua fluye fuera del tanque. Nuestro objetivo es medir la velocidad a la que están cambiando todas estas variables. Los derivados ayudan a medir la tasa de cambio de las cantidades. Veamos cómo formularlos y usarlos, 

Definición de Derivados

Digamos que tenemos una función f(x), que queremos observar. La derivada de esta función nos dirá la velocidad a la que está cambiando esta función con respecto a su entrada. La derivada de una función f(x) se denota por f'(x) o  \frac{d(f(x))}{dx}. Las derivadas se definen utilizando el concepto de límites. 

Digamos que f es una función de valor real y ‘a’ es un punto en su dominio de definición. La derivada de f en a se define como, 

f'(a) =\lim_{h \to 0} \frac{f(a + h) -f(a)}{h}

Dado que sus límites existen. 

Esto también se conoce como [\frac{df}{dx}]_{x = a}

El diagrama anterior representa la interpretación geométrica de la derivada. Tengamos dos puntos P(a, f(a)) y Q(a + h, f(a + h)) que están cerca uno del otro en el gráfico. Sabemos que según la definición, 

f'(a) =\lim_{h \to 0} \frac{f(a + h) -f(a)}{h}

Del triángulo PQR, es claro que la razón cuyo límite estamos tomando es exactamente igual a tan(QPR) que es la pendiente de la cuerda PQ. En el proceso de limitación, como h tiende a 0, el punto Q tiende a P, y tenemos, 

\lim_{h \to 0} \frac{f(a + h) -f(a)}{h} = lim_{Q \to P}\frac{QP}{QR}

Podemos ver que la cuerda PQ tiende a ser tangente a la curva f(x). El límite es igual a la pendiente de la tangente a la curva en el punto particular. 

Ejemplo: Encuentra la derivada de f(x) = 3x en x = 2. 

Solución: 

f'(2) = \lim_{h \to 0}\frac{f(x + h) - f(x)}{h}  

f'(2) = \lim_{h \to 0}\frac{3(x + h) - 3x}{h}

⇒ f'(2) = \lim_{h \to 0}\frac{3h}{h}

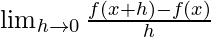
⇒ f'(2) = 3

Álgebra de Derivadas

Dado que las derivadas involucran límites, se espera que sigan las propiedades de los límites. Digamos que tenemos dos funciones «f» y «g». Veamos las propiedades de sus derivados. 

  • La derivada de la suma de dos funciones es igual a la suma de las derivadas de las dos funciones. 

\frac{d}{dx}[f(x) + g(x)] = \frac{d}{dx}f(x) + \frac{d}{dx}g(x)

  • Derivadas de la diferencia entre dos funciones es la diferencia de las derivadas de las dos funciones. 

\frac{d}{dx}[f(x) - g(x)] = \frac{d}{dx}f(x) - \frac{d}{dx}g(x)

  • Las derivadas del producto de dos funciones vienen dadas por las reglas del producto de las derivadas. 

\frac{d}{dx}[f(x).g(x)] = g(x)\frac{d}{dx}f(x) + f(x)\frac{d}{dx}g(x)

  • Derivadas de la división de las dos funciones se da la regla del cociente de las derivadas. 

\frac{d}{dx}[\frac{f(x)}{g(x)}] = \frac{g(x)\frac{d}{dx}f(x) - f(x)\frac{d}{dx}g(x)}{g(x)^2}

Encontrar la ecuación de tangentes usando derivadas

Digamos que tenemos una función y = f(x). Necesitamos encontrar la ecuación de la tangente a esta curva en x = a. Ya sabemos que la derivada en un punto determinado nos da la pendiente de la tangente. Entonces, tenemos los puntos (a, f(a)) y la pendiente de la tangente. Podemos formar la ecuación de la línea como se indica a continuación, 

Digamos la derivada de la función en x = a, . Sabemos que la ecuación de la recta es  \frac{dy}{dx} = f'(x)

y = mx + b, 

donde m = ,  \frac{dy}{dx} = f'(x)

y = x + segundo \frac{dy}{dx}

Ahora sustituyendo el punto (a,f(a)) en lugar de (x,y) en la ecuación anterior. 

f(a) = a+ b \frac{dy}{dx}

⇒ b = f(a) –  \frac{dy}{dx}a

Por lo tanto, la ecuación de la línea se convierte en, 

y = x + f(a) –  a \frac{dy}{dx} \frac{dy}{dx}

Veamos algunos ejemplos de problemas sobre estos conceptos. 

Problemas de muestra

Pregunta 1: Encuentra la derivada de la función f(x) = x 2 en x = 0. 

Solución:

f'(x) = \lim_{h \to 0}\frac{f(x + h) - f(x)}{h}  

f'(x) = \lim_{h \to 0}\frac{(x + h)^2 - x^2}{h}

⇒ f'(x) = \lim_{h \to 0}\frac{(x^2 + h^2 + 2hx - x^2)}{h}

⇒ f'(x) = \lim_{h \to 0}h + 2x

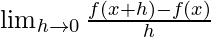
⇒ f'(x) = 2x

f'(0) = 0

Pregunta 2: Encuentra la derivada de la función f(x) = x 2 en x = 2. 

Solución:

f'(x) = \lim_{h \to 0}\frac{f(x + h) - f(x)}{h}  

f'(x) = \lim_{h \to 0}\frac{(x + h)^2 - x^2}{h}

⇒ f'(x) = \lim_{h \to 0}\frac{(x^2 + h^2 + 2hx - x^2)}{h}

⇒ f'(x) = \lim_{h \to 0}h + 2x

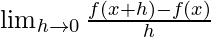
⇒ f'(x) = 2x

f'(2) = 4

Pregunta 3: Encuentra la derivada de la función f(x) = x 2 + x +1 en x = 0. 

Solución:

f'(x) = \lim_{h \to 0}\frac{f(x + h) - f(x)}{h}  

f'(x) = \lim_{h \to 0}\frac{((x + h)^2 + (x +h) + 1) - (x^2 + x + 1)}{h}

⇒ f'(x) = \lim_{h \to 0}\frac{((x^2 + h^2 + 2hx + (x +h) + 1) - (x^2 + x + 1)}{h}

⇒ f'(x) = \lim_{h \to 0}\frac{(h^2 + 2hx +h)}{h}

⇒ f'(x) = \lim_{h \to 0}(h + 2x +1)

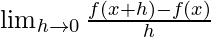
⇒f'(x) = 2x + 1

f'(0) = 1 

Pregunta 4: Encuentra la derivada de la función f(x) = e x en x = 0. 

Solución: 

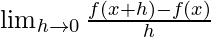
f'(x) = \lim_{h \to 0}\frac{f(x + h) - f(x)}{h}  

f'(x) = \lim_{h \to 0}\frac{e^{(x + h)} - e^x}{h}

⇒ f'(x) = \lim_{h \to 0}\frac{e^xe^h - e^x}{h}

⇒ f'(x) = e^x\lim_{h \to 0}\frac{(e^h - 1)}{h}

Esta es la forma 0/0 del límite. Lo sabemos \lim_{h \to 0}\frac{(e^h - 1)}{h} = 1

⇒ f'(x) = e^x\lim_{h \to 0}\frac{e^h }{1}

⇒ f'(x) = e^x (1)

⇒f'(x) =e x

f'(0) = 1 

Observe que la derivada de la función exponencial es exponencial en sí misma. 

Pregunta 5: Encuentra la ecuación de la tangente en el punto x = 0 para la función dada f(x) = x 2 + 1. 

Solución:

Sabemos que, f(x) =x 2 + 1

f(1) = 2

Entonces, la tangente pasa por (0,2). Ahora, para encontrar la pendiente de la tangente, calculemos la derivada de esta función. 

f'(x) = \lim_{h \to 0}\frac{f(x + h) - f(x)}{h}  

f'(x) = \lim_{h \to 0}\frac{(x+h)^2 + 1 - x^2 -1}{h}

⇒ f'(x) = \lim_{h \to 0}\frac{x^2 +h^2 + 2hx + 1 - x^2 -1}{h}

⇒ f'(x) = \lim_{h \to 0}\frac{h^2 + 2hx}{h}

⇒ f'(x) = \lim_{h \to 0}h + 2x

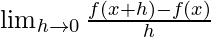
⇒ f'(x) = 2x

f'(1) = 2

Entonces, la pendiente de la tangente = 2. 

Ecuación general de recta 

y = mx + b 

donde m = 2, todavía no sabemos b 

y = 2x + b 

Sabemos que esta recta pasa por (0,2) 

2 = 2(0) + segundo

⇒ 2 = segundo 

Por lo tanto, la ecuación de la tangente es 

y = 2x + 2

Pregunta 6: Encuentra la derivada de f(x) = x 2 + e x . 

Responder:

f(x) = x 2 + e x

Sabemos que esta función está formada por dos términos, por las preguntas anteriores sabemos las derivadas de estos dos términos individualmente. 

Entonces, usando las propiedades mencionadas anteriormente, 

\frac{d}{dx}[f(x) + g(x)] = \frac{d}{dx}f(x) + \frac{d}{dx}g(x)

Podemos descomponer esta función en diferentes funciones, calcular sus derivadas y sumarlas. 

Digamos f(x) = g(x) + h(x) 

Donde g(x) = x 2 y h(x) = e x . Las derivadas de estas funciones ya han sido calculadas en las preguntas anteriores, 

g'(x) = 2x y h'(x) = e x . 

f'(x) = g'(x) + h'(x) 

f'(x) = 2x + e x

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *