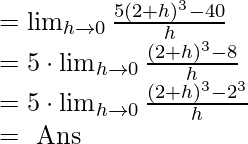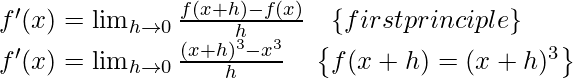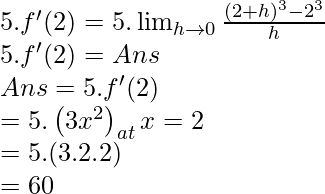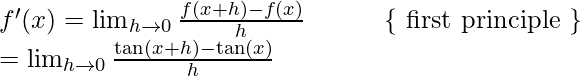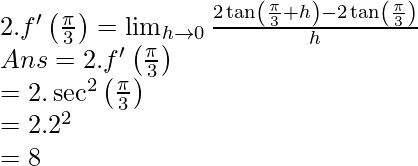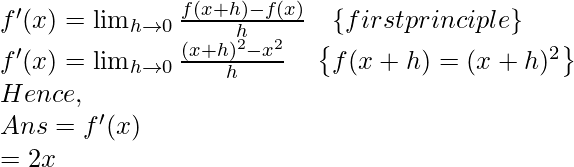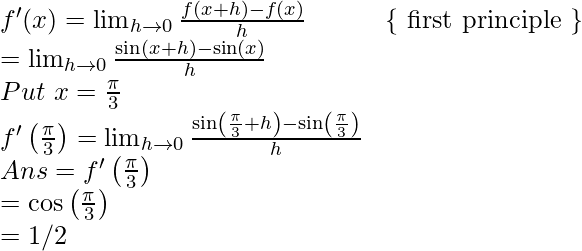Derivados disfrazados: diferenciación avanzada | Clase 12 Matemáticas

El significado del diccionario de » disfrazar» es » irreconocible». Derivado encubierto significa “ derivado no reconocido”. En este tipo de problemas, la definición de derivada se oculta en forma de límite. De un vistazo, el problema parece resolverse usando propiedades límite, pero es mucho más fácil resolverlo usando el primer principio de la derivada. Entonces, este tipo de problemas se conocen como derivados disfrazados.

Antes de continuar, necesitamos revisar el primer principio de la derivada. Encontrar la derivada de una función calculando este límite se conoce como diferenciación a partir de primeros principios. La derivada por primer principio se refiere al uso del álgebra para encontrar una expresión general para la pendiente de una curva. También se conoce como el método delta. La derivada es una medida de la tasa de cambio instantánea, que es igual a

$\begin{aligned} \ \ \ \ \ \ \ \ \ f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \end{aligned}$

Método para resolver

Paso 1. Intenta simplificar la ecuación de tal manera que se asemeje al primer principio de la derivada.

Paso 2. Encuentra el valor de f(x)

Paso 3. Encuentra f'(x) usando el primer principio.

Paso 4. Encuentra el valor de x tal que al sustituirlo se asemeje a la pregunta

Entendámoslo mejor usando un problema de ejemplo.

Ejemplos de problemas sobre derivadas encubiertas

Ejemplo 1.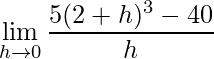 $\begin{aligned} \qquad &\lim _{h \rightarrow 0} \frac{5(2+h)^{3}-40}{h} \end{aligned}$

Solución:

Este tipo de problemas se pueden resolver mediante la evaluación límite y la diferenciación. Entendamos ambas soluciones una por una y luego comparemos cuál es mejor.

Solución usando evaluación límite:

$\\ \begin{array}{l} \qquad =\lim _{h \rightarrow 0} \frac{5\left(2^{3}+h^{3}+3.2 \cdot h(2+h)\right)-40}{h} \\ \qquad =\lim _{h \rightarrow 0} \frac{40+5 h^{3}+30 h(2+h)-40}{h} \\ \qquad =\lim _{h \rightarrow 0} \frac{5 h^{3}+60 h+30 h^{2}}{h} \\ \qquad =\lim _{h \rightarrow 0} 5 h^{2}+60+30 h \\ \qquad =0+60+0 \\ \qquad =60 \end{array}$

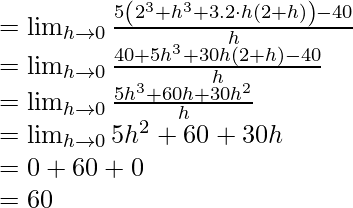
Ahora tenemos la respuesta a nuestro problema, es decir, 60. Esta función no era demasiado complicada y la evaluación de límites no era tan difícil. Entonces, este enfoque funciona bastante bien. Pero en variaciones más duras sería realmente complicado evaluar el límite. Nuestra intención principal en el segundo método sería tratar de simplificar la ecuación de tal manera que se asemeje al primer principio de la derivada.

Solución usando diferenciación:

Simplifique el problema dado:

$\\ \qquad=\lim _{h \rightarrow 0} \frac{5(2+h)^{3}-40}{h} \\ \qquad=5 \cdot \lim _{h \rightarrow 0} \frac{(2+h)^{3}-8}{h} \\ \qquad=5 \cdot \lim _{h \rightarrow 0} \frac{(2+h)^{3}-2^{3}}{h} \\ \qquad=\text { Ans }$
Tomemos f(x)=x ³
$\\ f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \quad\{first principle \} \\f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{(x+h)^{3}-x^{3}}{h} \quad\left\{f(x+h)=(x+h)^{3}\right\}$
Poniendo x=2 en ambos lados,
$\\f^{\prime}(2)=\lim _{h \rightarrow 0} \frac{(2+h)^{3}-2^{3}}{h}$
Multiplique ambos lados por 5,
$\\5 . f^{\prime}(2)=5 . \lim _{h \rightarrow 0} \frac{(2+h)^{3}-2^{3}}{h} \\5 . f^{\prime}(2) =A n s \\ \ \ \ \ \ A n s =5 . f^{\prime}(2) \\ \ \ \ \ \ \ \ \ \ \ =5 .\left(3 x^{2}\right)_{a t} x=2 \\ \ \ \ \ \ \ \ \ \ \ =5 .(3.2 .2) \\ \ \ \ \ \ \ \ \ \ \ =60$

La belleza de este método radica en conocer f(x). El límite de aspecto complicado era un derivado disfrazado. Por lo tanto, si tiene alguna dificultad para comprender el proceso, vuelva a realizarlo. Sería mucho más claro después de resolver algunos ejemplos más.

Ejemplo 2. $\\ \qquad\lim _{h \rightarrow 0} \frac{2 \tan \left(\frac{\pi}{3}+h\right)-2 \tan \left(\frac{\pi}{3}\right)}{h}$

Solución:

Tome f(x) = tan(x)
$\\ \qquad f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\qquad \quad\{\text { first principle }\} \\ \ \ \qquad\qquad=\lim _{h \rightarrow 0} \frac{\tan (x+h)-\tan (x)}{h}$
Ponga x= $\frac{\pi}{3}$ y multiplique ambos lados por 2,
$\\ \qquad2. f^{\prime}\left(\frac{\pi}{3}\right)=\lim _{h \rightarrow 0} \frac{2 \tan \left(\frac{\pi}{3}+h\right)-2 \tan \left(\frac{\pi}{3}\right)}{h}\\ \qquad \qquad A n s =2 . f^{\prime}\left(\frac{\pi}{3}\right) \\ \qquad \qquad \qquad =2 . \sec ^{2}\left(\frac{\pi}{3}\right) \\ \qquad \qquad \qquad =2.2^{2} \\ \qquad \qquad \qquad =8$

Ejemplo 3.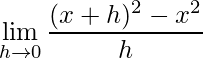 $\\ \begin{aligned} \qquad &\lim _{h \rightarrow 0} \frac{(x+h)^{2}-x^2}{h} \end{aligned}$

Solución:

Tomemos f(x) = x ²
$\\ f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \quad\{first principle \} \\f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{(x+h)^{2}-x^{2}}{h} \quad\left\{f(x+h)=(x+h)^{2}\right\} \\Hence, \\ \qquad Ans=f'(x) \\ \qquad \qquad \ =2x$

Ejemplo 4. $\\ \lim _{h \rightarrow 0} \frac{ \sin \left(\frac{\pi}{3}+h\right)- \sin \left(\frac{\pi}{3}\right)}{h}$

Solución:

Tome f(x) = sen(x)
$\\ \qquad f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\qquad \quad\{\text { first principle }\} \\ \ \ \qquad\qquad=\lim _{h \rightarrow 0} \frac{\sin (x+h)-\sin (x)}{h} \\ \qquad Put\ x=\frac{\pi}{3}\ \\ \qquad f^{\prime}\left(\frac{\pi}{3}\right)=\lim _{h \rightarrow 0} \frac{ \sin \left(\frac{\pi}{3}+h\right)- \sin \left(\frac{\pi}{3}\right)}{h} \\ \qquad \qquad A n s = f^{\prime}\left(\frac{\pi}{3}\right) \\ \qquad \qquad \qquad = \cos\left(\frac{\pi}{3}\right) \\ \qquad \qquad \qquad =1/2$

Publicación traducida automáticamente

Artículo escrito por rathoreatul27 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Método para resolver

Ejemplos de problemas sobre derivadas encubiertas

Deja una respuesta Cancelar la respuesta