Los codificadores automáticos variacionales beta fueron propuestos por investigadores de Deepmind en 2017. Fue aceptado en la Conferencia internacional sobre representaciones de aprendizaje (ICLR) 2017. Antes de aprender el codificador automático variacional beta, consulte este artículo para conocer el codificador automático variacional.
Si en el codificador automático variacional, si cada variable es sensible a solo una característica/propiedad del conjunto de datos y relativamente invariable a otra propiedad, entonces se llama representación desenredada del conjunto de datos. La ventaja de tener una representación desenredada es que el modelo es fácil de generalizar y tiene buena interpretabilidad. Este es el objetivo principal de los autocodificadores variacionales beta, es decir, lograr el desenredo. Por ejemplo, una red neuronal entrenada en los rostros humanos para determinar el género de esa persona necesita capturar diferentes características del rostro (como el ancho del rostro, el color del cabello, el color de los ojos) en dimensiones separadas para asegurar el desenredo.
B-VAE agrega un parámetro B al autocodificador variacional que actúa como equilibrio entre la capacidad latente del Node y la restricción independiente con precisión de reconstrucción. La motivación detrás de agregar este hiperparámetro es maximizar la probabilidad de generar un conjunto de datos reales mientras que minimizar la probabilidad de datos reales a estimados es pequeña, por debajo de 
.
Para escribir la siguiente ecuación, necesitamos usar la condición de Kuhn-Tucker.
![\mathcal{F}\left(\theta, \phi, \beta; \mathbf{x}, \mathbf{z}\right) = \mathbb{E}_{q_{\phi}\left(\mathbf{z}|\mathbf{x}\right)}\left[\log{p}_{\theta}\left(\mathbf{x}\mid\mathbf{z}\right)\right] - \beta\left[D_{KL}\left(\log{q}_{\theta}\left(\mathbf{z}\mid\mathbf{x}\right)||p\left(\mathbf{z}\right)\right) - \epsilon\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2952a8bb42594611463bfdabfc5a492c_l3.png "Rendered by QuickLaTeX.com")
donde el multiplicador KKT 
es el coeficiente de regularización que restringe la capacidad del canal latente z y ejerce una presión de independencia implícita sobre el posterior aprendido debido a la naturaleza isotrópica del previo gaussiano p(z) .
Ahora, escribimos esto nuevamente usando la suposición de holgura complementaria anterior para obtener la fórmula Beta-VAE:
![\mathcal{F}\left(\theta, \phi, \beta; \mathbf{x}, \mathbf{z}\right) \geq \mathcal{L}\left(\theta, \phi, \beta; \mathbf{x}, \mathbf{z}\right) = \mathbb{E}_{q_{\phi}\left(\mathbf{z}|\mathbf{x}\right)}\left[\log{p}_{\theta}\left(\mathbf{x}\mid\mathbf{z}\right)\right] - \beta{D}_{KL}\left(\log{q}_{\theta}\left(\mathbf{z}\mid\mathbf{x}\right)||p\left(\mathbf{z}\right)\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72576b03ea1ccbf25fe1d9d23d48cf63_l3.png "Rendered by QuickLaTeX.com")
Beta-VAE intenta aprender una representación desenredada mediante factores generativos de datos condicionalmente independientes mediante la optimización de una divergencia KL muy penalizadora entre las distribuciones anterior y aproximada mediante un hiperparámetro β > 1 .
![max_{\phi,\theta}E_{x \propto D}\left [ E_{z \sim q_{\phi}(z|x)} log p_{\theta} (x|z) \right ] \\ subject \, to \, D_{Kl}(q_{\phi}(z|x) || p_{\theta} (z) ) < \delta](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a908d03535315a3068332d1b2b17d330_l3.png "Rendered by QuickLaTeX.com")
Podemos reescribir la ecuación anterior con el multiplicador Beta de Lagrange bajo la condición kkT. La ecuación anterior es igual a la siguiente condición de optimización:
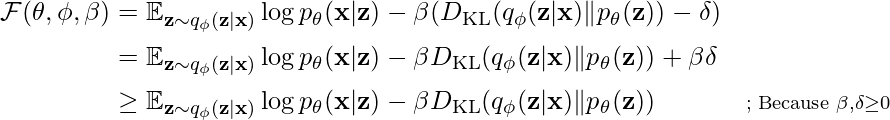
Arquitectura:
La arquitectura Beta codificador automático variacional tiene una arquitectura similar en comparación con el codificador automático variacional (excepto por el parámetro beta). La configuración completa contiene dos codificadores y decodificadores de redes. El codificador toma una imagen como entrada y genera la representación latente, mientras que el decodificador toma esa representación latente e intenta reconstruir la imagen. Aquí, las representaciones latentes están representadas por la distribución normal que contiene dos variables: media y varianza. Pero el decodificador requiere solo una representación latente. Esto se hace tomando muestras de la distribución normal.
Arquitectura Beta-VAE
Desenredo en B-VAE:
El B-VAE está estrechamente relacionado con el principio InfoGAIN, lo que significa que la máxima información que se puede almacenar es:
![max[I(Z;Y) - \beta I(Z;Y)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-427fd728fa229ea330616c36bcbef4b6_l3.png "Rendered by QuickLaTeX.com")
donde, I es información mutua y beta es el multiplicador de Lagrange, aquí el objetivo de esta función es maximizar la información latente entre el cuello de botella latente Z y la tarea Y mientras se descarta toda la información irrelevante sobre Y que podría estar presente en la entrada.
Los autores experimentaron con la arquitectura considerando la distribución posterior q(z|x) como un cuello de botella de información para la tarea de reconstrucción. Llegaron a la conclusión de que la distribución posterior transmite de manera eficiente información sobre el punto de datos x al minimizar el término KL ponderado β y maximizar la probabilidad de registro de datos.
En este VAE, se recomienda que la distribución posterior coincida con la unidad anterior gaussiana (distribución normal). Dado que el posterior y el anterior están factorizados, el posterior se puede calcular utilizando el truco de la reparametrización, podemos adoptar una perspectiva de teoría de la información y pensar en q(z|x) como un conjunto de canales de ruido gaussiano blanco aditivos independientes z i , cada uno ruidosamente transmitiendo información sobre las entradas de datos x n .
Ahora, el término de divergencia KL del objetivo β-VAE 
es un límite superior en la cantidad de información que se puede transmitir a través de los canales latentes por muestra de datos. La divergencia KL es cero cuando
q( zi |x) = p (z) , es decir, µi siempre es cero, y σi es siempre 1, lo que significa que los canales latentes zi tienen capacidad cero .
Por lo tanto, la capacidad de los canales latentes solo se puede aumentar dispersando las medias posteriores a través de los puntos de datos o disminuyendo las variaciones posteriores, que aumentan el término de divergencia KL.