Dada una array A[] que consta de los caracteres ‘U’ , ‘D’ , ‘L’ y ‘R’ que representan direcciones arriba , abajo , izquierda y derecha , y otra array B[] que consta de N enteros positivos, la tarea es encontrar el desplazamiento de un robot, comenzando su viaje desde (0, 0) mirando hacia el norte , después de N movimientos , donde en el i -ésimo movimiento , el robot se mueve una distancia B[i] en la dirección A[i].
Ejemplos:
Entrada: A[] = {U, R, R, R, R}, B[] = {1, 1, 1, 1, 0}
Salida: 0 Norte
Explicación:
Inicialmente, el robot está en (0, 0) mirando al norte.
Después del primer movimiento, la posición es (0, 1) mirando al Norte.
Después del segundo movimiento, la posición es (1, 1) mirando hacia el Este.
Después del tercer movimiento, la posición es (1, 0) mirando al Sur.
Después del cuarto movimiento, la posición es (0, 0) mirando hacia el Oeste.
Después del quinto movimiento, la posición es (0, 0) mirando al Norte.Por lo tanto, el desplazamiento es 0 y la dirección final es el Norte.
Entrada: A[] = {U, L, R, D, R}, B[] = {5, 5, 5, 5, 5}
Salida: 11 Oeste
Enfoque: el problema dado se puede resolver atravesando la array dada y manteniendo la pista de la dirección y la distancia recorrida en la dirección Norte (N) , Sur (S) , Este (E) y Oeste (O) . Siga los pasos a continuación para resolver el problema:
- Inicialice las variables, digamos N , S , E y W que almacenan las distancias recorridas en las direcciones Norte , Sur , Este y Oeste , respectivamente, después de un conjunto dado de movimientos.
- Inicialice una variable, digamos P como Norte , que almacene la dirección final después de realizar el conjunto de movimientos dado.
- Recorra las arrays dadas A[] y B[] simultáneamente y actualice el valor de la distancia recorrida en todas las direcciones con la dirección actual.
- Ahora, el desplazamiento vertical viene dado por (N – S) y el desplazamiento horizontal viene dado por (E – S) .
- Después de completar los pasos anteriores, imprima el desplazamiento final como
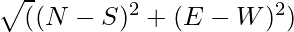y la dirección final almacenada en P .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to find the displacement
// from the origin and direction after
// performing the given set of moves
void finalPosition(char a[], int b[],
int M)
{
// Stores the distances travelled
// in the directions North, South,
// East, and West respectively
int n = 0, s = 0, e = 0, w = 0;
// Store the initial
// position of robot
char p = 'N';
// Traverse the array B[]
for (int i = 0; i < M; i++) {
// If the current
// direction is North
if (p == 'N') {
if (a[i] == 'U') {
p = 'N';
n = n + b[i];
}
else if (a[i] == 'D') {
p = 'S';
s = s + b[i];
}
else if (a[i] == 'R') {
p = 'E';
e = e + b[i];
}
else if (a[i] == 'L') {
p = 'W';
w = w + b[i];
}
}
// If the current
// direction is South
else if (p == 'S') {
if (a[i] == 'U') {
p = 'S';
s = s + b[i];
}
else if (a[i] == 'D') {
p = 'N';
n = n + b[i];
}
else if (a[i] == 'R') {
p = 'W';
w = w + b[i];
}
else if (a[i] == 'L') {
p = 'E';
e = e + b[i];
}
}
// If the current
// direction is East
else if (p == 'E') {
if (a[i] == 'U') {
p = 'E';
e = e + b[i];
}
else if (a[i] == 'D') {
p = 'W';
w = w + b[i];
}
else if (a[i] == 'R') {
p = 'S';
s = s + b[i];
}
else if (a[i] == 'L') {
p = 'N';
n = n + b[i];
}
}
// If the current
// direction is West
else if (p == 'W') {
if (a[i] == 'U') {
p = 'W';
w = w + b[i];
}
else if (a[i] == 'D') {
p = 'E';
e = e + b[i];
}
else if (a[i] == 'R') {
p = 'N';
n = n + b[i];
}
else if (a[i] == 'L') {
p = 'S';
s = s + b[i];
}
}
}
// Stores the total
// vertical displacement
int ver_disp = n - s;
// Stores the total
// horizontal displacement
int hor_disp = e - w;
// Find the displacement
int displacement = floor(
sqrt((ver_disp * ver_disp)
+ (hor_disp * hor_disp)));
// Print the displacement and
// direction after N moves
cout << displacement << " " << p;
}
// Driver Code
int main()
{
char A[] = { 'U', 'R', 'R', 'R', 'R' };
int B[] = { 1, 1, 1, 1, 0 };
int N = sizeof(A) / sizeof(B[0]);
finalPosition(A, B, N);
return 0;
}
Java
// Java program for the above approach
class GFG{
// Function to find the displacement
// from the origin and direction after
// performing the given set of moves
static void finalPosition(char[] a, int[] b, int M)
{
// Stores the distances travelled
// in the directions North, South,
// East, and West respectively
int n = 0, s = 0, e = 0, w = 0;
// Store the initial
// position of robot
char p = 'N';
// Traverse the array B[]
for(int i = 0; i < M; i++)
{
// If the current
// direction is North
if (p == 'N')
{
if (a[i] == 'U')
{
p = 'N';
n = n + b[i];
}
else if (a[i] == 'D')
{
p = 'S';
s = s + b[i];
}
else if (a[i] == 'R')
{
p = 'E';
e = e + b[i];
}
else if (a[i] == 'L')
{
p = 'W';
w = w + b[i];
}
}
// If the current
// direction is South
else if (p == 'S')
{
if (a[i] == 'U')
{
p = 'S';
s = s + b[i];
}
else if (a[i] == 'D')
{
p = 'N';
n = n + b[i];
}
else if (a[i] == 'R')
{
p = 'W';
w = w + b[i];
}
else if (a[i] == 'L')
{
p = 'E';
e = e + b[i];
}
}
// If the current
// direction is East
else if (p == 'E')
{
if (a[i] == 'U')
{
p = 'E';
e = e + b[i];
}
else if (a[i] == 'D')
{
p = 'W';
w = w + b[i];
}
else if (a[i] == 'R')
{
p = 'S';
s = s + b[i];
}
else if (a[i] == 'L')
{
p = 'N';
n = n + b[i];
}
}
// If the current
// direction is West
else if (p == 'W')
{
if (a[i] == 'U')
{
p = 'W';
w = w + b[i];
}
else if (a[i] == 'D')
{
p = 'E';
e = e + b[i];
}
else if (a[i] == 'R')
{
p = 'N';
n = n + b[i];
}
else if (a[i] == 'L')
{
p = 'S';
s = s + b[i];
}
}
}
// Stores the total
// vertical displacement
int ver_disp = n - s;
// Stores the total
// horizontal displacement
int hor_disp = e - w;
// Find the displacement
int displacement = (int)Math.ceil(Math.sqrt(
(ver_disp * ver_disp) + (hor_disp * hor_disp)));
// Print the displacement and
// direction after N moves
System.out.print(displacement + " " + p);
}
// Driver Code
public static void main(String args[])
{
char[] A = { 'U', 'R', 'R', 'R', 'R' };
int[] B = { 1, 1, 1, 1, 0 };
int N = 1;
finalPosition(A, B, N);
}
}
// This code is contributed by abhinavjain194
Python3
# Python3 program for the above approach from math import sqrt, floor # Function to find the displacement # from the origin and direction after # performing the given set of moves def finalPosition(a, b, M): # Stores the distances travelled # in the directions North, South, # East, and West respectively n = 0 s = 0 e = 0 w = 0 # Store the initial # position of robot p = 'N' # Traverse the array B[] for i in range(M): # If the current # direction is North if (p == 'N'): if (a[i] == 'U'): p = 'N' n = n + b[i] elif (a[i] == 'D'): p = 'S' s = s + b[i] elif (a[i] == 'R'): p = 'E' e = e + b[i] elif (a[i] == 'L'): p = 'W' w = w + b[i] # If the current # direction is South elif (p == 'S'): if (a[i] == 'U'): p = 'S' s = s + b[i] elif(a[i] == 'D'): p = 'N' n = n + b[i] elif(a[i] == 'R'): p = 'W' w = w + b[i] elif(a[i] == 'L'): p = 'E' e = e + b[i] # If the current # direction is East elif(p == 'E'): if (a[i] == 'U'): p = 'E' e = e + b[i] elif (a[i] == 'D'): p = 'W' w = w + b[i] elif (a[i] == 'R'): p = 'S' s = s + b[i] elif (a[i] == 'L'): p = 'N' n = n + b[i] # If the current # direction is West elif (p == 'W'): if (a[i] == 'U'): p = 'W' w = w + b[i] elif (a[i] == 'D'): p = 'E' e = e + b[i] elif (a[i] == 'R'): p = 'N' n = n + b[i] elif (a[i] == 'L'): p = 'S' s = s + b[i] # Stores the total # vertical displacement ver_disp = n - s # Stores the total # horizontal displacement hor_disp = e - w # Find the displacement displacement = floor(sqrt((ver_disp * ver_disp) + (hor_disp * hor_disp)) + 1) # Print the displacement and # direction after N moves print(displacement,p) # Driver Code if __name__ == '__main__': A = [ 'U', 'R', 'R', 'R', 'R' ] B = [ 1, 1, 1, 1, 0 ] N = len(A) finalPosition(A, B, N) # This code is contributed by ipg2016107
C#
// C# program for the above approach
using System;
class GFG{
// Function to find the displacement
// from the origin and direction after
// performing the given set of moves
static void finalPosition(char[] a, int[] b, int M)
{
// Stores the distances travelled
// in the directions North, South,
// East, and West respectively
int n = 0, s = 0, e = 0, w = 0;
// Store the initial
// position of robot
char p = 'N';
// Traverse the array B[]
for(int i = 0; i < M; i++)
{
// If the current
// direction is North
if (p == 'N')
{
if (a[i] == 'U')
{
p = 'N';
n = n + b[i];
}
else if (a[i] == 'D')
{
p = 'S';
s = s + b[i];
}
else if (a[i] == 'R')
{
p = 'E';
e = e + b[i];
}
else if (a[i] == 'L')
{
p = 'W';
w = w + b[i];
}
}
// If the current
// direction is South
else if (p == 'S')
{
if (a[i] == 'U')
{
p = 'S';
s = s + b[i];
}
else if (a[i] == 'D')
{
p = 'N';
n = n + b[i];
}
else if (a[i] == 'R')
{
p = 'W';
w = w + b[i];
}
else if (a[i] == 'L')
{
p = 'E';
e = e + b[i];
}
}
// If the current
// direction is East
else if (p == 'E')
{
if (a[i] == 'U')
{
p = 'E';
e = e + b[i];
}
else if (a[i] == 'D')
{
p = 'W';
w = w + b[i];
}
else if (a[i] == 'R')
{
p = 'S';
s = s + b[i];
}
else if (a[i] == 'L')
{
p = 'N';
n = n + b[i];
}
}
// If the current
// direction is West
else if (p == 'W')
{
if (a[i] == 'U')
{
p = 'W';
w = w + b[i];
}
else if (a[i] == 'D')
{
p = 'E';
e = e + b[i];
}
else if (a[i] == 'R')
{
p = 'N';
n = n + b[i];
}
else if (a[i] == 'L')
{
p = 'S';
s = s + b[i];
}
}
}
// Stores the total
// vertical displacement
int ver_disp = n - s;
// Stores the total
// horizontal displacement
int hor_disp = e - w;
// Find the displacement
int displacement = (int)Math.Ceiling(Math.Sqrt(
(ver_disp * ver_disp) + (hor_disp * hor_disp)));
// Print the displacement and
// direction after N moves
Console.WriteLine(displacement + " " + p);
}
// Driver Code
public static void Main()
{
char[] A = { 'U', 'R', 'R', 'R', 'R' };
int[] B = { 1, 1, 1, 1, 0 };
int N = 1;
finalPosition(A, B, N);
}
}
// This code is contributed by ukasp
Javascript
<script>
// Javascript program for the above approach
// Function to find the displacement
// from the origin and direction after
// performing the given set of moves
function finalPosition(a, b, M)
{
// Stores the distances travelled
// in the directions North, South,
// East, and West respectively
let n = 0, s = 0, e = 0, w = 0;
// Store the initial
// position of robot
let p = 'N';
// Traverse the array B[]
for(let i = 0; i < M; i++)
{
// If the current
// direction is North
if (p == 'N')
{
if (a[i] == 'U')
{
p = 'N';
n = n + b[i];
}
else if (a[i] == 'D')
{
p = 'S';
s = s + b[i];
}
else if (a[i] == 'R')
{
p = 'E';
e = e + b[i];
}
else if (a[i] == 'L')
{
p = 'W';
w = w + b[i];
}
}
// If the current
// direction is South
else if (p == 'S')
{
if (a[i] == 'U')
{
p = 'S';
s = s + b[i];
}
else if (a[i] == 'D')
{
p = 'N';
n = n + b[i];
}
else if (a[i] == 'R')
{
p = 'W';
w = w + b[i];
}
else if (a[i] == 'L')
{
p = 'E';
e = e + b[i];
}
}
// If the current
// direction is East
else if (p == 'E')
{
if (a[i] == 'U')
{
p = 'E';
e = e + b[i];
}
else if (a[i] == 'D')
{
p = 'W';
w = w + b[i];
}
else if (a[i] == 'R')
{
p = 'S';
s = s + b[i];
}
else if (a[i] == 'L')
{
p = 'N';
n = n + b[i];
}
}
// If the current
// direction is West
else if (p == 'W')
{
if (a[i] == 'U')
{
p = 'W';
w = w + b[i];
}
else if (a[i] == 'D')
{
p = 'E';
e = e + b[i];
}
else if (a[i] == 'R')
{
p = 'N';
n = n + b[i];
}
else if (a[i] == 'L')
{
p = 'S';
s = s + b[i];
}
}
}
// Stores the total
// vertical displacement
let ver_disp = n - s;
// Stores the total
// horizontal displacement
let hor_disp = e - w;
// Find the displacement
let displacement = Math.ceil(Math.sqrt(
(ver_disp * ver_disp) + (hor_disp * hor_disp)));
// Print the displacement and
// direction after N moves
document.write(displacement + " " + p);
}
let A = [ 'U', 'R', 'R', 'R', 'R' ];
let B = [ 1, 1, 1, 1, 0 ];
let N = 1;
finalPosition(A, B, N);
// This code is contributed by suresh07.
</script>
Producción:
1 N
Complejidad temporal: O(N)
Espacio auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por bhavanikonderu y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA