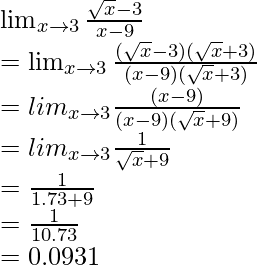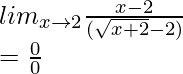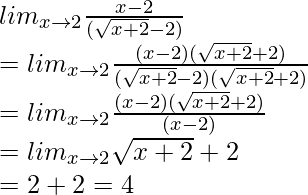Determinación de límites usando manipulación algebraica

se mueve

Un límite es un valor al que se acerca la función o la secuencia cuando la entrada o el índice se acercan a algún valor. Estos conceptos son esenciales en cálculo y análisis real, ya que nos ayudan a definir continuidad, diferenciabilidad e integrales. En la fórmula, el límite para una función f(x) en un punto x = c generalmente se denota como,

$\lim_{x \to c} f(x)$

A menudo, solo el método de sustitución es suficiente para calcular el límite. Pero a veces algunos límites pueden evaluar formas indeterminadas.

Formas indeterminadas

Por lo general, se encuentra una forma indeterminada cuando el límite involucra más de una función. Se define como una expresión que involucra a dos o más cuyo límite no puede determinarse únicamente a partir de las funciones individuales.

Las formas indeterminadas más comunes se generan a partir de los límites de razón de funciones, $\frac{f(x)}{g(x)}$ , cuando ambas funciones se evalúan como 0 o ∞ generando los límites de la forma $\frac{0}{0}$ o $\frac{\infty}{\infty}$ . Otras formas indeterminadas incluyen 0 x ∞, ∞ – ∞, 0 ^∞ etc.

Ciertos métodos algebraicos pueden ayudarnos a evitar estas formas.

Límites mediante manipulación algebraica

Estas técnicas del álgebra pueden ayudar a evitar las formas indeterminadas en los límites. Algunas de estas formas incluyen la evaluación de límites mediante la factorización y, a veces, la racionalización. En el caso de las funciones trigonométricas, algunos otros trucos como usar la identidad de Pitágoras o el límite trigonométrico usando la identidad de doble ángulo pueden ayudarnos a resolver estos límites.

Límites por factorización

Por lo general, en las funciones de razón que consisten en polinomios, la forma indeterminada proviene de uno de los factores que aparecen en la expresión. Por ejemplo, en la función f(x) dada a continuación, la forma indeterminada se debe al factor (x – 1).

$\lim_{x \to 1}\frac{x^2 - 1}{x - 1}$

En tales casos, factorizamos ambos polinomios de modo que el factor común se cancela.

$\lim_{x \to 1}\frac{x^2 - 1}{x - 1}$

⇒ $\lim_{x \to 1}\frac{(x - 1)(x + 1)}{x - 1}$

⇒ $\lim_{x \to 1}(x + 1)$

⇒ $\lim_{x \to 1}(1 + 1)$

⇒ 2

Límites por racionalización

En este método, la forma indeterminada se trata mediante la racionalización de la función.

$\lim_{x \to \infty} \sqrt{x^2 + x + 1} - \sqrt{x^2 + 1}$

Note que esto genera la forma indeterminada de ∞ – ∞.

En tales casos, racionalizamos la expresión.

$\lim_{x \to \infty} \sqrt{x^2 + x + 1} - \sqrt{x^2 + 1}$

⇒ $\lim_{x \to \infty} (\sqrt{x^2 + x + 1} - \sqrt{x^2 + 1})\frac{(\sqrt{x^2 + x + 1} + \sqrt{x^2 + 1})}{(\sqrt{x^2 + x + 1} + \sqrt{x^2 + 1})}$

⇒ $\lim_{x \to \infty} \frac{(x^2 + x + 1 - (x^2 + 1))}{(\sqrt{x^2 + x + 1} + \sqrt{x^2 + 1})}$

⇒ $\lim_{x \to \infty} \frac{x}{(\sqrt{x^2 + x + 1} + \sqrt{x^2 + 1})}$

⇒ $\lim_{x \to \infty} \frac{x}{(x\sqrt{1 + \frac{1}{x} + \frac{1}{x^2}} + \sqrt{1 + \frac{1}{x^2}})}$

⇒ $\lim_{x \to \infty} \frac{1}{(\sqrt{1 + \frac{1}{x} + \frac{1}{x^2}} + \sqrt{1 + \frac{1}{x^2}})}$

⇒ $\frac{1}{(\sqrt{1 + \frac{1}{\infty} + \frac{1}{\infty^2}} + \sqrt{1 + \frac{1}{\infty^2}})}$

⇒ $\frac{1}{2}$

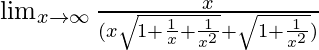
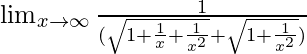
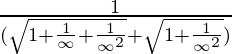
Límites trigonométricos utilizando identidades pitagóricas

Las identidades pitagóricas consisten en las siguientes tres identidades:

sen ² x + cos ² x = 1

1 + bronceado ² x = segundo ² x

1 + cuna ² x = cosec ² x

Estas identidades pueden usarse para sustituir en las funciones cuando las funciones trigonométricas muestran formas indeterminadas.

Identidades de doble ángulo

Las siguientes identidades de doble ángulo también se pueden usar para la sustitución en funciones trigonométricas:

cos2x = 2cos ² x – 1 = 1 – 2sen ² x

sen2x = 2senxcosx

Veamos algunos ejemplos de estos conceptos.

Problemas de muestra

Pregunta 1: Averigüe el siguiente límite.

$\lim_{x \to 1}\frac{x^2 -3x + 2}{x^2 - 1}$

Solución:

$\lim_{x \to 1}\frac{x^2 -3x + 2}{x^2 - 1}$

Este límite es de la forma 0/0. La factorización se puede utilizar aquí.

$\lim_{x \to 1}\frac{x^2 -3x + 2}{x^2 - 1}$

⇒ $\lim_{x \to 1}\frac{x^2 -2x -x + 2}{x^2 - 1^2}$

⇒ $\lim_{x \to 1}\frac{x(x -2) -1(x - 2)}{(x- 1)(x + 1)}$

⇒ $\lim_{x \to 1}\frac{(x - 1)(x -2)}{(x- 1)(x + 1)}$

⇒ $\lim_{x \to 1}\frac{(x -2)}{(x + 1)}$

⇒ $\lim_{x \to 1}\frac{(1 -2)}{(1 + 1)}$

⇒ $\frac{-1}{2}$

Pregunta 2: Averigüe el siguiente límite.

$\lim_{x \to 2}\frac{x^2 -5x + 6}{x^2 -3x +2}$

Solución:

$\lim_{x \to 2}\frac{x^2 -5x + 6}{x^2 -3x +2}$

Este límite es de la forma 0/0. La factorización se puede utilizar aquí.

$\lim_{x \to 2}\frac{x^2 -5x + 6}{x^2 -3x +2}$

⇒ $\lim_{x \to 2}\frac{x^2 -3x -2x + 6}{x^2 -x -2x +2}$

⇒ $\lim_{x \to 2}\frac{(x -3)(x -2)}{(x -1)(x-2)}$

⇒ $\lim_{x \to 2}\frac{(x -3)}{(x -1)}$

⇒ $\lim_{x \to 2}\frac{(2 -3)}{(2 -1)}$

⇒ -1

Pregunta 3: Averigüe el siguiente límite.

$\lim_{x \to 3}\frac{\sqrt{x} - 3}{x -9}$

Solución:

$\lim_{x \to 3}\frac{\sqrt{x} - 3}{x -9}$

Este límite es de forma indeterminada. La racionalización se puede utilizar aquí.

$\lim_{x \to 3}\frac{\sqrt{x} - 3}{x -9}\\=\lim_{x\to3}\frac{(\sqrt{x}-3)(\sqrt{x}+3)}{(x-9)(\sqrt{x}+3)}\\=lim_{x\to3}\frac{(x-9)}{(x-9)(\sqrt{x}+9)}\\=lim_{x\to3}\frac{1}{\sqrt{x}+9}\\=\frac{1}{1.73+9}\\=\frac{1}{10.73}\\=0.0931$

Pregunta 4: Averigüe el límite de,

$lim_{x\to2}\frac{x-2}{(\sqrt{x+2}-2)}$

Solución:

Poniendo el límite x tiende a 2 para ver el valor obtenido,

$lim_{x\to2}\frac{x-2}{(\sqrt{x+2}-2)}\\=\frac{0}{0}\\$

= Indefinido.

Como es claro que la respuesta es indefinida, racionaliza el denominador,

$lim_{x\to2}\frac{x-2}{(\sqrt{x+2}-2)}\\=lim_{x\to2}\frac{(x-2)(\sqrt{x+2}+2)}{(\sqrt{x+2}-2)(\sqrt{x+2}+2)}\\=lim_{x\to2}\frac{(x-2)(\sqrt{x+2}+2)}{(x-2)}\\=lim_{x\to2}\sqrt{x+2}+2\\=2+2=4$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Límites mediante manipulación algebraica

Problemas de muestra

Deja una respuesta Cancelar la respuesta