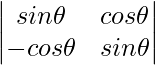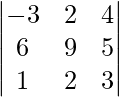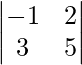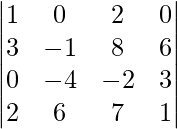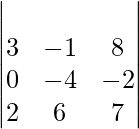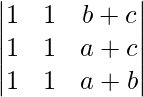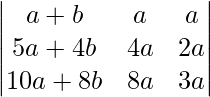La array es uno de los temas esenciales en matemáticas. Comprender el determinante de una array requiere un conocimiento básico de filas, columnas, etc. similares a arrays. El determinante de array se usa en varias fórmulas, como encontrar el inverso de una array y muchas más. Es fácil encontrar determinantes usando la fórmula del determinante. Tiene varias propiedades. Comprendamos cómo se determina el determinante de una array con la ayuda de la fórmula del determinante.
Determinante
El determinante de una array es un número único asociado con esa array cuadrada. El determinante de una array se puede calcular solo para una array cuadrada. Si A =[a ij ] es una array cuadrada de orden n, entonces el determinante de A está representado por det A o |A|. La representación general del determinante de la array A es,
det A o |A| o 
Fórmula determinante
- Determinante de una array cuadrada de orden 1
Si A = [a ij ] es una array cuadrada de orden 1, entonces el determinante de A se define como,
|A| = un 11
- Determinante de una array cuadrada de orden 2
Si A = 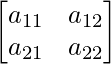 es una array cuadrada de orden 2, entonces el determinante se define como,
es una array cuadrada de orden 2, entonces el determinante se define como,
|A| = un 11 un 22 – un 12 un 21
- Determinante de una array cuadrada de orden 3
Si A =  es una array cuadrada de orden 2, entonces el determinante se define como,
es una array cuadrada de orden 2, entonces el determinante se define como,
|A| = 
|A| = (-1) 1+1 a 11  + (-1) 1+2 a 12
+ (-1) 1+2 a 12 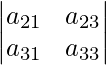 + (-1) 1+3 a 13
+ (-1) 1+3 a 13 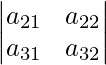
|A| = un 11  – un 12
– un 12 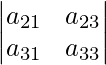 + un 13
+ un 13 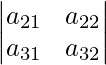
|A| = un 11 (un 22 un 33 – un 23 un 32 ) – un 12 (un 33 un 21 – un 23 un 31 ) + un 13 (un 32 un 21 – un 22 un 31 ) ⇢ (1)
|A| = un 11 un 22 un 33 + un 12 un 23 un 31 + un 13 un 32 un 21 – un 11 un 23 un 32 – un 22 un 13 un 31 – un 12 un 21 un 33
Así, el determinante de una array cuadrada de orden 3 es la suma del producto de los elementos a ij en la i -ésima fila con (-1) i+j por el determinante de una subarray de 2 x 2 obtenida al dejar la i- ésima fila y j -ésima columna que pasa por el elemento. La expansión se realiza a través de los elementos de i- ésima fila. Entonces, se conoce como la expansión a lo largo de la i- ésima fila. La expansión anterior (1) de |A| se conoce como la expansión a lo largo de la primera fila.
Nota
- Solo las arrays cuadradas tienen determinantes. Las arrays que no son cuadradas no tienen determinantes.
- El determinante de orden tres se puede expandir a lo largo de cualquier fila y columna.
- Si una fila o columna de un determinante son todos ceros, entonces el determinante es cero.
Menor
Considere una array cuadrada A =[a ij ] de orden n. El menor M ij de a ij en A determina la subarray cuadrada de orden (n – 1) que se obtiene al salir de la i-ésima fila y la j-ésima columna de A.
cofactor
Considere una array cuadrada A = [aij] de orden n. El cofactor C ij de a ij en A es igual a (-1)i + j por el menor M ij de a ij .
C ij = Cofactor de a ij en A = (-1) i+j M ij
Donde M ij es el menor de a ij en A.
Cij = _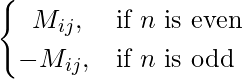
Array singular
Se dice que una array cuadrada es singular si su determinante es cero. De lo contrario, es no singular.
Propiedades del Determinante
Sea A una array cuadrada de orden n,
- La suma del producto de los elementos de cualquier fila (columna) con sus cofactores es igual a |A|.
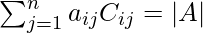 y
y 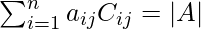
- La suma del producto de los elementos de cualquier fila(columna) con los cofactores de los elementos correspondientes de alguna otra fila(columna) es cero.
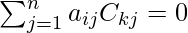 y
y 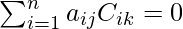
- El determinante permanece sin cambios si sus filas y columnas se intercambian (transposición). |A| =|A T |
- Si se intercambian dos filas (columnas), el determinante cambia por un signo menos. |B| = -|A| (B es una array obtenida al intercambiar dos filas (columnas) de A).
- Si dos filas o columnas de A son iguales, entonces su determinante es cero. |A| = 0
- Si B es la array obtenida al multiplicar el valor escalar k en cada elemento de la fila o columna de la array A, entonces |B| = k|A| .
- Si cada elemento de fila (o columna) es cero, entonces el determinante es cero.
- Si A es una array diagonal, entonces |A| = un 11 × un 22 × …. un nn _
- Si A y B son arrays cuadradas del mismo orden, entonces |AB| = |A||B|.
- Si cada elemento de una fila (columna) se puede expresar como la suma de dos o más términos, entonces el determinante se puede expresar como la suma de dos o más determinantes.
- Si B es una array obtenida sumando a una fila (columna) de A un múltiplo escalar de otra fila (columna) de A, entonces |B| = |A|.
Evaluación de Determinante
La evaluación del determinante de una array de orden 2 es fácil. Aun así, para una array de orden superior, la evaluación del determinante se puede hacer más accesible al realizar una operación de fila o columna para hacer que toda la fila o columna sea cero o idéntica o para hacer que más elementos sean cero para que el cálculo en la evaluación del determinante se vuelve más fácil.
Ejemplos de preguntas
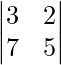
Pregunta 1: Evaluar:
Solución:
= (-2) × 3 – 6 × 4 = -30
= sen 2 θ – (-cos 2 θ) = sen 2 θ + cos 2 θ = 1
Pregunta 2: Evaluar:
- D =
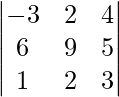 expandir a lo largo de la primera fila.
expandir a lo largo de la primera fila. - D=
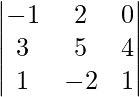 expandir a lo largo de la segunda columna.
expandir a lo largo de la segunda columna.
Solución:
- re=
= (-1) 1 + 1 (-3)
+ (-1) 1+2 (2)
+ (-1) 1+3 (4)
= -3
– 2
+ 4
= -3[9 × 3 – 5 × 10 ] – 2[6 × 3 – 5 × 1] + 4[6 × 2 – 9 × 1] = -3[27 -10] – 2[18 -5] + 4[12 -9] = -3 × 17 – 2 × 13 + 4 × 3 = -51 -26 +12 = -65
- re =
= (-1) 1 + 2 (2)
+ (-1) 2+2 (5)
+ (-1) 3+2 (-2)
= -2
+ 5
+ 2
= -2[3 × 1 – 4 × 1] + 5[1 × 1 – 1 × 0] + 2[(-1) × 5 – 2 × 3] = -2[3 – 4] + 5[1 – 0] + 2[-5 – 6] = (-2) × (-1) + 5 × 1 + 2 × (-11) = (-2) × (-1) + 5 × 1 + 2 × (- 11)
= 2 + 5 – 22 = -15
Pregunta 3: Evaluar: D = 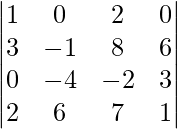 expandir a lo largo de la primera fila.
expandir a lo largo de la primera fila.
Solución:
re =
D = (-1) 1+1 (1)
+ (-1) 1+2 (0)
+ (-1) 1+3 (2)
+ (-1) 1+4 (0)
D = 1[(-1) 1+1 (-1)
+ (-1) 1+2 (8)
+(-1) 1+3 (6)
] – 0 +2[(-1) 1+1 (3)
+ (-1) 1+2 (-1)
+(-1) 1+3 (6)
] – 0
D = 1[(-1){(-2} × 1 – 3 × 7} – 8{(-4) × 1 – 6 × 3} + 6{(-4) × 7 – 6 × (-2) }] + 2[3{(-4} × 1 – 6 × 3} + 1{0 × 1 – 3 × 2} + 6{0 × 6 -(-4) × 2}]
D = [-1 × (-2 – 21) – 8 × (-4 – 18) + 6(-28 + 12)] + 2[3 × (-4 – 18) + (0 – 6) + 6 × (0 + 8)]
re = [-1 × (-23) – 8 × (-22) + 6 × (-16)] + 2[3 × (-22) -6 + 48]
D = [23 + 176 – 96] + 2[-66 – 6 + 48]
D = 103 + 2 × (-24) = 103 – 48
re = 55
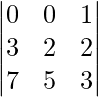
Pregunta 4: Encuentra el valor de x para el cual la array A =  es singular.
es singular.
Solución:
La array A es singular, si |A| = 0
= 0
⇒ 1
+ 2
+ 3
= 0
⇒ (-6 – 2) + 2(-3 – x) + 3(2 – 2x) = 0
⇒ -8 – 6 – 2x + 6 – 6x = 0
⇒ -8x – 8 = 0
⇒ x = -1
Pregunta 5: Demuestra que 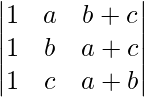 =0.
=0.
Solución:
re =
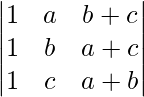
Aplicar C 2 ⇢ C 2 + C 3
re =
D = (a+ b+ c)
D = (a+ b+ c) x 0 = 0 [Dado que C 1 y C 2 son idénticos, entonces determinante = 0 (Propiedad del determinante)]
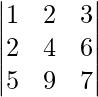
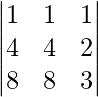
Pregunta 6: Evaluar: 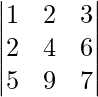
Solución:
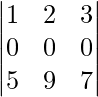
re =
R 2 ⇢ R 2 – 2R 1
re =
[Puesto que todos los elementos de R2 son 0 entonces, D = 0]
re = 0
Pregunta 7: Demostrar que : 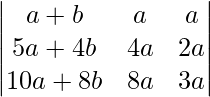 = a 3
= a 3
Solución:
Sea D =
Dado que C 2 contiene la suma de dos elementos, se puede representar como la suma de dos determinantes.
re =
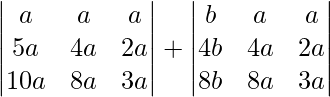
Tomando a y b comunes de filas y columnas.
D = a 3
+ ba 2
Como C 1 y C 2 en el segundo determinante son iguales, su determinante es cero.
re = un 3
+ ba 2 × 0
Aplicando C 1 ⇢ C 1 – C 3 , C 2 ⇢ C 2 – C 3
re = un 3
re = un 3 × 1 ×
re = un 3 (15 – 14) = un 3
Publicación traducida automáticamente
Artículo escrito por aayushi2402 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA