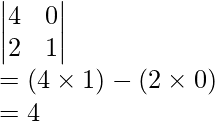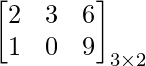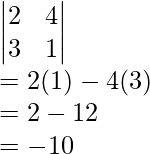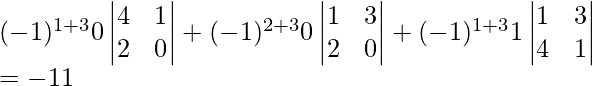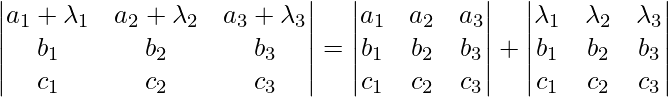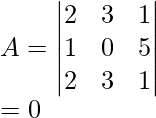Determinante de una array

Posted on by Rudeus Greyrat

En el estudio de álgebra y arrays, un sistema de ecuaciones lineales suele expresarse en forma de arrays. Por ejemplo, 

un 1 x + segundo 1 y + c 1 = 0

un 2 x + segundo 2 x + c 2 = 0 

Un sistema como este también se puede expresar como, 

\begin{bmatrix} a_{1} & b_{1}\\ a_{2} & b_{2} \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} =\begin{bmatrix} c_{1}\\ c_{2} \end{bmatrix}

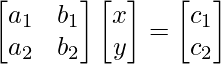
Ahora bien, este sistema de ecuaciones tiene solución única o no, está determinada por el número a 1 b 2 – a 2 b 1 . Esta cantidad que determina la unicidad de la solución se llama determinante. Se utiliza ampliamente en los campos de la informática y la ingeniería eléctrica. Los determinantes también nos dan una idea sobre el área o el volumen del espacio. Para resolver Determinantes, primero debemos comprender algunos términos, como Menores y Cofactores . Aprendamos sobre ellos.

menores

Se requiere Minor para encontrar el determinante de los elementos individuales (cada elemento) de la array. Son los determinantes de cada elemento obtenidos al eliminar las filas y columnas de ese elemento. Si la array dada es:

\begin{bmatrix}a_{11} & a_{12} &a_{13}\\a_{21} & a_{22} & a_{23}\\a_{31} & a_{32} & a_{33}\end{bmatrix}

El Menor de un 12 será el determinante:

\begin{vmatrix}a_{21} & a_{23}\\a_{31} & a_{33}\end{vmatrix}

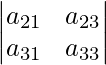
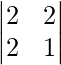
Pregunta: Encuentra el Menor de 5 en el determinante 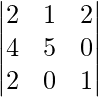\begin{vmatrix}2 & 1 & 2\\4 & 5 & 0\\2 & 0 & 1\end{vmatrix}

Responder: 

El menor de 5 será el determinante de \begin{vmatrix}2 & 2\\2 & 1\end{vmatrix}

Calculando el determinante, el menor se obtiene como: 

(2 × 1) – (2 × 2) = -2

cofactores

Los cofactores están relacionados con los menores por una pequeña fórmula, para un elemento a ij , el cofactor de este elemento es C ij y el menor es M ij entonces, el cofactor se puede escribir como: 

C ij = (-1) i+j M ij

Pregunta: Encuentra el cofactor del elemento colocado en la primera fila y segunda columna del determinante:

\begin{vmatrix}2 & 1 & 2\\4 & 5 & 0\\2 & 0 & 1\end{vmatrix}

Responder: 

Para encontrar el cofactor del elemento de la primera fila y la segunda columna, es decir, el cofactor de 1. Primero averigüe el menor de 1, que será: 

\begin{vmatrix}4 & 0\\2 & 1\end{vmatrix} \\ = (4 \times 1) - (2 \times 0) \\ = 4

METRO 12 = 4

Ahora, aplicando la fórmula para el cofactor: 

C 12 = (-1) 1 + 2 METRO 12

⇒ C12 = (-1) 3 × 4

⇒ C12 = -4

adjunto

La Adjunta de una array de orden n se puede definir como la transpuesta de sus cofactores. Para una array A:

adj. A = [ Cij ] n×n T

Transposición de una array

La transposición de una array A se denota como AT o A’. Es claro que el lado vertical en la array se conoce como columna y el lado horizontal se conoce como fila, Transponer una Array significa reemplazar las Filas por columnas y Viceversa, ya que las Filas y las Columnas van cambiando, el Orden de Matrix también cambia.

 Si una Array se da como A= [a ij ] m×n , entonces su Transposición se convertirá en A T o A’ = [a ji ] n×m

Pregunta: ¿Cuál será la transposición de la Matrix:

\begin{bmatrix}2 & 1\\3 & 0\\6 & 9\end{bmatrix}_{2\times3}

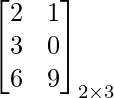
Responder: 

Intercambio de filas y columnas, AT = \begin{bmatrix}2 & 3 & 6\\1 & 0 & 9\end{bmatrix}_{3\times2}

 Determinante

Un determinante es un número asociado a toda array cuadrada A = [a ij ] de orden n. El determinante de la array A se denota por |A| o det(A). 

Si A =  \begin{bmatrix} a & b \\ c & d \end{bmatrix}, su determinante se denota por \begin{vmatrix} a & b \\ c & d \end{vmatrix}

Importancia física del determinante

Considere una array 2D, cada columna de esta array se puede considerar como un vector en el plano xy. Entonces, el determinante entre dos vectores en un plano 2d nos da el área encerrada entre ellos. Si ampliamos este concepto, en 3D el determinante nos dará el volumen encerrado entre dos vectores. 

Área encerrada entre dos vectores en 2D

Determinante de una array de Orden Uno

Sea X = [a] la array de orden uno, entonces su determinante viene dado por det(X) = a. 

Determinante de una array de Orden Dos

Sea X =  \begin{bmatrix} a & b \\ c & d \end{bmatrix}, su determinante viene dado por la multiplicación cruzada de sus elementos. 

det(X) = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc

Pregunta: Evalúa A = 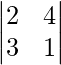\begin{vmatrix} 2 & 4 \\ 3 & 1 \end{vmatrix}

Responder: 

un = \begin{vmatrix} 2 & 4 \\ 3 & 1 \end{vmatrix} \\ = 2(1) - 4(3) \\ = 2 - 12 \\ = -10

Determinante de una array de Orden 3×3

Se puede determinar expresándolo en términos de determinantes de segundo orden. Se puede expandir a lo largo de filas (R1, R2 o R3) o columnas (C1, C2 o C3). Considere una array A de orden 3. 

un = 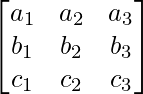\begin{bmatrix} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{bmatrix}  

Paso 1: Multiplicar el primer elemento a11 de la fila R1 por (-1)(1 + 1)[(-1)suma de sufijos en a11] y con el determinante de segundo orden obtenido al eliminar los elementos de la fila R1 y C1 de A ya que a11 se encuentra en R1 y C1. 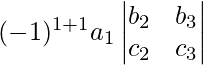(-1)^{1 + 1}a_{1}\begin{vmatrix} b_{2} & b_{3} \\ c_{2} & c_{3} \end{vmatrix}

Paso 2: Del mismo modo, multiplica el segundo elemento de la primera fila R1, con el determinante obtenido después de eliminar la primera fila y la segunda columna. (-1)^{1 + 2}a_{12}\begin{vmatrix} b_{1} & b_{3} \\ c_{1} & c_{3} \end{vmatrix}

Paso 3: Multiplique el tercer elemento de la fila R1 con el determinante obtenido después de eliminar la primera fila y la tercera columna. 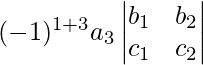(-1)^{1 + 3}a_{3}\begin{vmatrix} b_{1} & b_{2} \\ c_{1} & c_{2} \end{vmatrix}

Paso 4: Ahora la expansión del determinante de A, que es |A| se puede escribir como |A| = 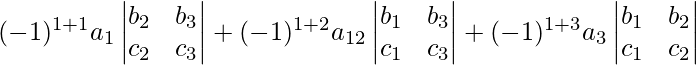 (-1)^{1 + 1}a_{1}\begin{vmatrix} b_{2} & b_{3} \\ c_{2} & c_{3} \end{vmatrix} + (-1)^{1 + 2}a_{12}\begin{vmatrix} b_{1} & b_{3} \\ c_{1} & c_{3} \end{vmatrix} + (-1)^{1 + 3}a_{3}\begin{vmatrix} b_{1} & b_{2} \\ c_{1} & c_{2} \end{vmatrix}

De igual forma, de esta forma, podemos expandirlo a lo largo de cualquier fila y cualquier columna. 

Pregunta: Evalúa el determinante det(A) = 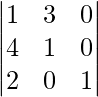\begin{vmatrix} 1 & 3 & 0 \\ 4 & 1 & 0 \\ 2 & 0 & 1 \end{vmatrix}

Responder: 

Vemos que la tercera columna tiene la mayor cantidad de ceros, por lo que será más fácil expandirse a lo largo de esa columna. 

det(A) = (-1)^{1 + 3}0\begin{vmatrix}4 & 1 \\ 2 & 0 \end{vmatrix} + (-1)^{2 + 3}0\begin{vmatrix}1 & 3 \\ 2 & 0 \end{vmatrix} + (-1)^{1 + 3}1\begin{vmatrix}1 & 3 \\ 4 & 1 \end{vmatrix} \\ = -11

Propiedades de los Determinantes

  • Propiedad de reflexión : el valor del determinante permanece sin cambios incluso después de intercambiar filas y columnas. Ese determinante de una array, y su transposición, sigue siendo el mismo.
  • Propiedad de cambio: si se intercambian dos filas o columnas cualesquiera de un determinante, entonces cambia el signo del determinante.

Por ejemplo: \begin{vmatrix} 3 & 3 & 0 \\ 2 & 1 & 1 \\ 5 & 0 & 1 \end{vmatrix}

det. A = [3×{(1×1)-(0×1)}]-[3×{(2×1)-(5×1)}]+[0×{(2×0)-(5 ×1)}]

= {3×(1-0)}-{3×(2-5)+0

= [3-{3(-3)}+0]

= (3+9)

=12

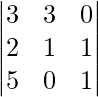
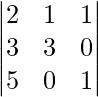
Ahora, intercambiando la fila 1 con la fila 2, el determinante será:

\begin{vmatrix} 2 & 1 & 1 \\ 3 & 3 & 0 \\ 5 & 0 & 1 \end{vmatrix}

det. A = [2×{(3×1)-(0×0)}]-[1×{(3×1)-(5×0)}]+[1×{(3×0)-(5 ×3)}]

= (6-3-15)

= -12

  • Propiedad de repetición/Propiedad de proporcionalidad: si dos filas o dos columnas de un determinante son idénticas, entonces el valor del determinante se convierte en cero.
  • Propiedad múltiple escalar: si cada elemento de una fila (o una columna) de un determinante se multiplica por una constante k, entonces su valor se multiplica por k

 \begin{vmatrix} ka & kb \\ c & d \end{vmatrix} = k\begin{vmatrix} a & b \\ c & d \end{vmatrix}

  • Propiedad de la suma : si algunos o todos los elementos de una fila o columna pueden expresarse como la suma de dos o más términos, entonces el determinante también puede expresarse como la suma de dos o más determinantes.

 \begin{vmatrix} a_{1} + \lambda_{1} & a_{2} + \lambda_{2} & a_{3} + \lambda_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{vmatrix} = \begin{vmatrix} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{vmatrix} + \begin{vmatrix} \lambda_{1} & \lambda_{2} & \lambda_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{vmatrix}

Ejemplos de propiedades

Pregunta 1: Si x, y, z son diferentes. y A = \begin{vmatrix} x & x^{2} & 1 + x^{3} \\ y & y^{2} & 1 + y^{3} \\ z & z^{2} & 1 + z^{3} \end{vmatrix} = 0 , luego demuestre que 1 + xyz = 0. 

Responder: 

Usando la propiedad de la suma:

 \begin{vmatrix} x & x^{2} & 1 + x^{3} \\ y & y^{2} & 1 + y^{3} \\ z & z^{2} & 1 + z^{3} \end{vmatrix} = \begin{vmatrix} x & x^{2} & 1 \\ y & y^{2} & 1\\ z & z^{2} & 1 \end{vmatrix} + \begin{vmatrix} x & x^{2} & x^{3} \\ y & y^{2} & y^{3} \\ z & z^{2} & z^{3} \end{vmatrix} \text{} \\ = (-1)^{2}\begin{vmatrix} 1 & x & x^{2} \\ 1 & y & y^{2}\\ 1 & z & z^{2} \end{vmatrix} + xyz\begin{vmatrix} 1 & x & x^{2} \\ 1 & y & y^{2}\\ 1 & z & z^{2} \end{vmatrix} \\ = (1 + xyz) \begin{vmatrix} 1 & x & x^{2} \\ 1 & y & y^{2}\\ 1 & z & z^{2} \end{vmatrix} = 0 

Al resolver este determinante y expandirlo, 

A = (1 + xyz)(y-x)(zy)(zx) 

Dado que se da en la pregunta, todos los x, y y z tienen valores diferentes y A = 0. Entonces, el único término que puede ser cero es 1 + xyz. 

Por lo tanto, 1 + xyz = 0

Pregunta 2: Evaluar  \begin{vmatrix} 102 & 18 & 36 \\ 1 & 3 & 4 \\ 17 & 3 & 6 \\ \end{vmatrix}. 

Responder: 

Uso de la propiedad múltiple escalar y la propiedad de repetición: 

 \begin{vmatrix} 102 & 18 & 36 \\ 1 & 3 & 4 \\ 17 & 3 & 6 \\ \end{vmatrix} = \begin{vmatrix} 17(6) & 6(3) & 6(6) \\ 1 & 3 & 4 \\ 17 & 3 & 6 \\ \end{vmatrix} \\ = 6\begin{vmatrix} 17 & 3 & 6 \\ 1 & 3 & 4 \\ 17 & 3 & 6 \\ \end{vmatrix} = 0 \text{}

Pregunta 3: Evalúa el determinante A. A = \begin{vmatrix} 2 & 3 & 1 \\ 1 & 0 & 5 \\ 2 & 3 & 1 \end{vmatrix} \\

Responder: 

Usando la propiedad de proporcionalidad:

Dos de las filas de la array son idénticas. 

Asi que, A = \begin{vmatrix} 2 & 3 & 1 \\ 1 & 0 & 5 \\ 2 & 3 & 1 \end{vmatrix} \\ = 0 \text{}

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *