Antes de entrar en el diagrama de riesgo de Weibull, primero comprendamos qué es una función de riesgo.
Función de riesgo (h(t)): Nos informa sobre la medida del riesgo de falla. Nos da información sobre la probabilidad de falla del objeto en un estudio en (t+1) tiempo, suponiendo que haya sobrevivido hasta el tiempo t. Entonces, cuanto mayor sea el valor de peligro, mayor será el riesgo de falla del objeto en estudio. Una función de peligro para cualquier objeto se representa como:
Diagrama de riesgo acumulativo: es una representación gráfica que proporciona información sobre la confiabilidad del modelo ajustado en el conjunto de datos dado. (es decir, al observar este gráfico, podemos encontrar fácilmente el tiempo de falla apropiado para un modelo. La función de riesgo acumulativo para la distribución de Weibull viene dada por:
![]()
where, H(t) -> failure rate t -> failure at time t γ -> shape parameter α -> scale parameter
Función de riesgo de Weibull
La distribución de weibull también tiene una función de riesgo h(t), que esencialmente nos brinda información previa sobre un evento que aún está por ocurrir. Pongamos un ejemplo para una mejor comprensión. Pongamos un ejemplo para una mejor comprensión.
Digamos que tenemos una antorcha que hemos estado usando durante el tiempo t. La probabilidad de que falle en algún momento entre t y t + dt horas de operación está dada por la función de riesgo de weibull. Con base en el diagrama de riesgo de Weibull, la función de riesgo para la antorcha se puede describir como:
![]()
Al igual que en el diagrama PPCC de Weibull, la función de riesgo h(t) también varía con el cambio en el parámetro de forma (γ) de la distribución. (Ver figura 1)

Figura 1: Gráfica H(t) vs t
Este gráfico funciona muy bien para las distribuciones de weibull de 2 parámetros que se han discutido en el artículo ‘Gráfico de Weibull’.
Estructura
El gráfico de riesgo de weibull tiene los siguientes parámetros en los ejes: (Ver Fig. 2)
Eje y: Logaritmo de la función de riesgo, ln(H(t)) .
Eje x: Logaritmo del tiempo, ln(t/α) .
γ sirve como la pendiente de este gráfico lineal.

Fig. 2: Estructura del diagrama de riesgo de Weibull
Trazado manual de un gráfico de riesgo de Weibull
Sabemos que la función de riesgo de Weibull es
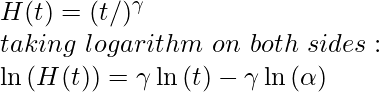
Al calcular los valores logarítmicos y trazar ln(H(t)) vs ln(t) plot , obtenemos un gráfico de tipo lineal. Por lo tanto, podemos determinar una buena estimación del valor del parámetro de forma γ a medida que se convierte en la pendiente de esa gráfica.
Implementación de código
Aquí está la implementación del código que muestra un diagrama de weibull y un diagrama de riesgo de weibull correspondiente.
import weibull as wb
# Creating a custom random data for failure points.
fails = [5002.7, 6203.4, 14367.2, 11144.6, 7332.0,
3044.4, 12330.2, 1234.5, 2553.9, 3632.1]
# analysis contains the data to be fit into the weibull plot.
Weibull_Analysis = wb.Analysis(fails, unit='minutes')
# fit() method used for fitting
# the data into weibull plot.
Weibull_Analysis.fit()
# printing the values of beta and eta (instances of Weibull_Analysis)
print(f'beta: {Weibull_Analysis.beta: .03f}')
print(f'eta: {Weibull_Analysis.eta: .03f}')
# probplot() method used
# for plotting the weibull distribution
Weibull_Analysis.probplot()
# hazard() method used for plotting
# Weibull Hazard Plot
print(Weibull_Analysis.hazard())
Producción

Salida 1: Diagrama de Weibull

Salida 2: Diagrama de riesgo de Weibull
Publicación traducida automáticamente
Artículo escrito por prakharr0y y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA