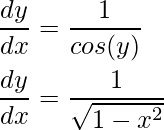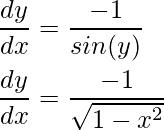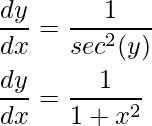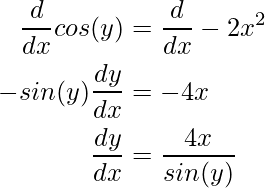En este artículo, exploraremos la aplicación de la derivación implícita para encontrar la derivada de funciones trigonométricas inversas. Pero antes de continuar, repasemos el concepto de diferenciación implícita y trigonometría inversa.
trigonometría inversa
Las funciones trigonométricas inversas son las funciones inversas de las razones trigonométricas, es decir, sin, cos, tan, cot, sec, cosec. Estas funciones se utilizan ampliamente en campos como la física, las matemáticas, la ingeniería y otros campos de investigación. Así como la suma y la resta son inversas entre sí, lo mismo ocurre con la inversa de las funciones trigonométricas.
sen θ = x
⇒ θ
Representación de funciones trigonométricas inversas
Se representan sumando arco en el prefijo o sumando -1 a la potencia.
El seno inverso se puede escribir de dos formas:
- pecado -1 x
- arcosen x
Lo mismo ocurre con cos y bronceado.
Nota: No confundas sen -1 x con (sen x) -1 . Ellos son diferentes. Escribir sen -1 x es una forma de escribir seno inverso mientras que (sen x) -1 significa 1/sen x.
Diferenciación implícita
La diferenciación implícita es un método que utiliza la regla de la string para diferenciar funciones implícitamente definidas. Por lo general, no es fácil encontrar la función explícitamente y luego diferenciarla. En cambio, podemos derivar totalmente f(x, y) y luego resolver el resto de la ecuación para encontrar el valor de f'(x). Incluso cuando es posible resolver explícitamente la ecuación original, la fórmula resultante de la diferenciación total es, en general, mucho más simple y fácil de usar. Diferenciamos algunas de las funciones trigonométricas inversas.
Ejemplo 1: ¿Derivar sen -1 (x)?
Solución:
Dejar,
Tomando seno en ambos lados de la ecuación da,
Por la propiedad de la trigonometría inversa sabemos,
Ahora diferenciando ambos lados con respecto a x,
Podemos simplificarlo más usando la siguiente observación:
Sustituyendo el valor, obtenemos
Ejemplo 2: ¿Derivar cos -1 (x)?
Solución:
Dejar,
Tomando coseno en ambos lados de la ecuación da,
Por la propiedad de la trigonometría inversa sabemos,
Ahora diferenciando ambos lados con respecto a x,
Podemos simplificarlo más usando la siguiente observación:
Sustituyendo el valor, obtenemos
Ejemplo 3: Diferenciar tan -1 (x)?
Solución:
Dejar,
Tomando tan en ambos lados de la ecuación da,
Por la propiedad de la trigonometría inversa sabemos,
Ahora diferenciando ambos lados con respecto a x,
Podemos simplificarlo más usando la siguiente observación:
Sustituyendo el valor, obtenemos
Algunos ejemplos avanzados de diferenciación de funciones de trigonometría inversa
Ejemplo 1: y = cos -1 (-2x 2 ). ¿Encuentra dy/dx en x = 1/2?
Solución:
Método 1 (usando diferenciación implícita)
Dado,
Diferenciando ambos lados wrt x
simplificando
Poniendo el valor obtenido obtenemos,
Método 2 (Usando la regla de la string ya que conocemos la diferenciación de arccos x)
Dado,
Diferenciando ambos lados wrt x
Ejemplo 2: Diferenciar  ?
?
Dejar,
Diferenciando ambos lados wrt x
|
Función |
Derivado |
|---|---|
Publicación traducida automáticamente
Artículo escrito por rathoreatul27 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA