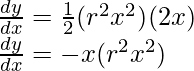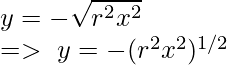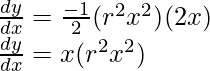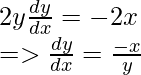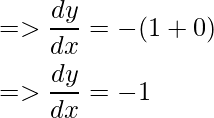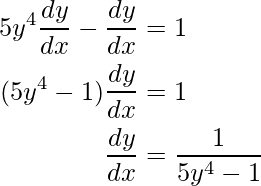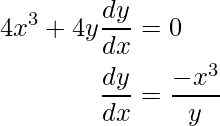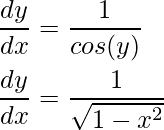Diferenciación implícita – Part 1

La diferenciación implícita es un método que utiliza la regla de la string para diferenciar funciones implícitamente definidas. Por lo general, no es fácil encontrar la función explícitamente y luego diferenciarla. En cambio, podemos derivar totalmente f(x, y) y resolver el resto de la ecuación para encontrar el valor de dy/dx. Incluso cuando es posible resolver explícitamente la ecuación original, la fórmula resultante de la diferenciación total es, en general, mucho más simple y fácil de usar. Antes de saltar al tema, echemos un vistazo a un problema de muestra. Esto te ayudará a entender los conceptos muy fácilmente.

Pregunta: ¿Encuentra la ecuación de la pendiente de la tangente en cualquier punto del círculo con centro en el origen?

Solución:

Para resolver este problema, necesitamos encontrar la ecuación de la función en términos de x (es decir, y = f(x)) y luego encontrar f'(x). Primero escribamos la ecuación general para un círculo.

x ² + y ² = r ²

En esta forma de la ecuación, la función se expresa en términos de y y x. Esta función se conoce como función implícita ya que y no se define explícitamente como una función de x, es decir, esta función no tiene la forma y = f(x). Encontremos la derivada explícitamente. Para resolver esto explícitamente,

Resolver la ecuación para y

diferenciar la función

Sustituir atrás y

En este caso,

x ² + y ² = r ²

Resta x ² de ambos lados:

y ² = r ² – x ²

Sacando raíz cuadrada en ambos lados:

y = ± $\sqrt{r^2 − x^2}$

Caso 1:

$y = +\sqrt{r^2 − x^2}$

=> y = ( r ² − x ² ) ^1/2

Derivada por regla de la string:

$\frac{dy}{dx} =\frac{1}{2}(r^2 − x^2)^{−½}(−2x)\\ \frac{dy}{dx} =-x(r^2 − x^2)^{−½}$

Ya que, $y = +\sqrt{r^2 − x^2} \\$

$=> \ \frac{dy}{dx} =\frac{-x}{y}$

Caso 2:

$y = -\sqrt{r^2 − x^2} \\=> \ y=-({r^2 − x^2})^{1/2} \\$

Derivada por regla de la string:

$\frac{dy}{dx} =\frac{-1}{2}(r^2 − x^2)^{−½}(−2x)\\ \frac{dy}{dx} =x(r^2 − x^2)^{−½}$

Ya que, $y = -\sqrt{r^2 − x^2} \\$

$\frac{dy}{dx} =\frac{x}{-y}$

En cualquier caso, la respuesta es la misma, es decir , dy/dx = – x/y

Pero nuestra intención principal en este artículo sería tratar de resolver el problema sin encontrar explícitamente el valor de f(x). En este caso, encontrar la función f(x) fue bastante fácil, pero no sería el mismo caso en otros lugares.

Prerrequisito Básico

Regla de la string: La regla de la string es una fórmula para calcular la derivada de una función compuesta. Es decir, si f y g son funciones diferenciables, entonces la regla de la string expresa la derivada de su compuesto f ∘ g como: f(g(x))’ = f'(g(x)) * g'(x)
Función implícita vs explícita: una función puede ser explícita o implícita:
- Explícito: y = f(x) ej. y = x ²
- Implícito: f(x, y) = 0 ej. y + x ² = 5

Aquí tomamos solo 2 variables x e y para definir la función implícita. Pero puede tener cualquier número de variables.

Método para resolver la diferenciación implícita

Derive ambos lados de la ecuación con respecto a x.
Sigue las reglas de diferenciación.
Usa la regla de la string para diferenciar expresiones que involucran y.
Resuelve la ecuación para dy/dx.

Ahora, resolveremos la pregunta anterior usando diferenciación implícita.

Solución:

Dada la ecuación anterior es:

x ² + y ² = r ²

Paso 1: Diferenciar ambos lados con respecto ax y seguir la diferenciación

$\frac{d}{dx}({x^2}+y^2) =\frac{d}{dx}r^2$

Paso 2: Usando la regla de la string

$2x+2y\frac{dy}{dx}=0$

Paso 3: simplifica la ecuación

$2y\frac{dy}{dx}=-2x \\ => \frac{dy}{dx}=\frac{-x}{y}$

Obtuvimos la misma respuesta esperada que en el caso de diferenciación explícita.

Hemos demostrado con éxito que la diferenciación implícita y explícita da el mismo resultado. Veamos algunos ejemplos más para entender el concepto claramente. A veces, la forma implícita funciona cuando la forma explícita es difícil o imposible. En todos los ejemplos siguientes tenemos que encontrar el valor de dy/dx.

Ejemplos

Ejemplo 1: ¿Encontrar la derivada de y + x + 5 = 0?

Solución:

Usando diferenciación explícita:

y + x + 5 = 0

=> y = -(x + 5)

$\begin{aligned}\\ => \frac{dy}{dx}&=-(1+0) \\=> \frac{dy}{dx}&=-1 \end{aligned}$

Usando diferenciación implícita:

y + x + 5 = 0

Diferenciando ambos lados wrt x

$\frac{dy}{dx}+1+0=0$

Aislar dy/dx

$\frac{dy}{dx}=-1$

Ejemplo 2: Encuentra la derivada de y ⁵ – y = x?

Solución:

Ecuación dada:

y ⁵ – y = x

$\begin{aligned} 5y^4\frac{dy}{dx}-\frac{dy}{dx}&=1 \\ (5y^4-1)\frac{dy}{dx}&=1 \\ \frac{dy}{dx}&=\frac{1}{5y^4-1} \end{aligned}$

Ejemplo 3: ¿Encuentra la derivada de 10x ⁴ – 18xy ² + 10y ³ = 48?

Solución:

Ecuación dada:

10x ⁴ – 18xy ² + 10y ³ = 48

Diferenciando ambos lados wrt x

$10(4x^3) − 18(x.2y\frac{dy}{dx} + y^2) + 10(3y^2 \frac{dy}{dx}) = 0$

(la diferenciación del término xy ² se explica a continuación)

Al simplificar obtenemos:

$40x^3 − 36xy \frac{dy}{dx} − 18y^2 + 30y^2 \frac{dy}{dx} = 0$

Manteniendo todos los términos relacionados con dy/dx a la izquierda y los demás términos a la derecha de la ecuación:

$−36xy \frac{dy}{dx} + 30y^2 \frac{dy}{dx} = −40x^3+ 18y^2$

$(30y^2−36xy)\frac{dy}{dx}= 18y^2 − 40x^3$

Dividiendo ambos lados por 2

$(15y^2−18xy) \frac{dy}{dx}=9y^2 − 20x^3$

Finalmente aislar dy/dx

$\bold{\frac{dy}{dx}=\frac{9y^2 − 20x^3}{15y^2−18xy}}$

Para el término xy ² usamos la regla del producto: (fg)’ = f g’ + f’ g

$\begin{aligned} (xy^2)' &= x(y^2)' + (x)'y^2 \\ &=x({2y\frac{dy}{dx}})+y^2 \\ &=2xy\frac{dy}{dx}+y^2 \end{aligned}$

Ejemplo 4: ¿Encontrar la derivada de x ⁴ + 2y ² = 8?

Solución:

Ecuación dada:

x4 ⁺ 2y2 = ⁸

$\begin{aligned} 4x^3+4y\frac{dy}{dx}&=0 \\ \frac{dy}{dx}&=\frac{-x^3}{y} \end{aligned}$

Ejemplo 5: ¿Encontrar la derivada de y = sen ^-1 (x)?

Solución:

Ecuación dada:

y = sen ^-1 (x)

=> sen y = x

$\begin{aligned} \frac{d}{dx}sin (y)&= \frac{d}{dx}x \\ cos (y)\frac{dy}{dx} &= 1 \\ \frac{dy}{dx}&=\frac{1}{cos(y)} \\ \end{aligned}$

Podemos simplificarlo más usando la siguiente observación:

sen ² ( y ) + cos ² ( y )

sabemos , _

pecado ( y ) = x

=> x ² + cos ² ( y ) = 1

=> cos ² ( y ) = 1 – x ²

=> porque ( y ) = $\sqrt{1-x^2}$

Sustituyendo el valor, obtenemos

$\begin{aligned} \frac{dy}{dx}&=\frac{1}{cos(y)} \\ \frac{dy}{dx}&=\frac{1}{\sqrt{1-x^2}} \end{aligned}$

Resumen

Para encontrar la derivada implícitamente (útil cuando una función no se puede resolver fácilmente para y):

Diferenciar con respecto a x
Recoge todos los dy/dx en un lado
Resolver para dy/dx

La diferenciación implícita puede ayudarnos a resolver funciones inversas. Para derivar una función inversa, repítela sin la inversa y luego usa la diferenciación implícita.

Publicación traducida automáticamente

Artículo escrito por rathoreatul27 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Prerrequisito Básico

Método para resolver la diferenciación implícita

Ejemplos

Resumen

Deja una respuesta Cancelar la respuesta