El método para encontrar la derivada de una función tomando primero el logaritmo y luego diferenciando se llama diferenciación logarítmica. Este método se utiliza especialmente cuando la función es de tipo . En este tipo de problema donde y es una función compuesta, primero necesitamos tomar un logaritmo, haciendo la función . Esto crea una situación en la que la diferenciación de la función del exponente fue bastante difícil, pero después de tomar el registro en ambos lados de la ecuación, podemos diferenciarla fácilmente usando las propiedades del logaritmo y la regla de la string. Este método también se conoce como diferenciación de funciones exponenciales compuestas. Este enfoque nos permite calcular la derivada de funciones exponenciales complejas de manera eficiente.
Fórmula de diferenciación logarítmica
La única restricción para usar reglas de diferenciación logarítmica es que f(x) y u(x) deben ser positivas ya que las funciones logarítmicas solo se definen para valores positivos.
Pasos para resolver problemas de diferenciación logarítmica
Estos son los pasos que se dan aquí para resolver encontrar la diferenciación de funciones logarítmicas:
- Toma de registro en ambos lados.
- Use la propiedad de registro para eliminar el exponente.
- Ahora diferencia la ecuación.
- Simplifica la ecuación obtenida.
- Vuelva a sustituir el valor de y.
A veces puede ser un poco complicado, pero mantén la calma y solo diferencia. Los siguientes son algunos ejemplos de diferenciación logarítmica.
Ejemplo 1: Encuentra la derivada de x x ?
Solución:
Sea y = x x
Paso 1: Tomando registro en ambos lados
Use la propiedad de registro para eliminar el exponente
ahora diferencia la ecuacion
Paso 4:
Paso 5:
Ejemplo 2: Encuentra la derivada de 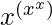 ?
?
Dado,
y =
Ejemplo 3: Encuentra la derivada de y = (log x) x ?
Ejemplo 4: Encuentra la derivada de y = x √x ?
Publicación traducida automáticamente
Artículo escrito por rathoreatul27 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA





