La palabra continuidad significa algo que es de naturaleza continua. El flujo de agua es continuo, el tiempo en la vida real es continuo y muchos más casos muestran la continuidad en la vida real. En matemáticas, la función continua es aquella que cuando se dibuja en un gráfico no muestra interrupciones y es de naturaleza continua. La diferenciabilidad de la función es posible solo y solo si es de naturaleza continua. La diferenciación logarítmica es un tema aparte debido a sus múltiples propiedades y para una mejor comprensión de Log.
Continuidad y Diferenciabilidad
La continuidad de una función muestra dos cosas, la propiedad de la función y el valor funcional de la función en cualquier punto. Se dice que una función es continua en x = a, si su valor permanece igual en x=a-, x=a+ y x=a. Más formalmente, se puede escribir como,
Se dice que una función es continua en el intervalo cerrado [a, b], si
- f es continua en (a, b)
- sigue

- sigue
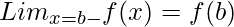
Diferenciabilidad significa que una función es diferenciable, si se dice que una función es diferenciable en x=a, significa que f'(a) [la derivada de la función] existe en todos y cada uno de los puntos de ese dominio.
Diferenciabilidad⇢ ![]()
Diferenciación logarítmica
La diferenciación logarítmica tiene su uso en muchos lugares de la física y las matemáticas, ya sea para resolver errores o resolver funciones muy complejas, se prefiere la diferenciación logarítmica a la diferenciación simple. El método tiene propiedades y reglas que cuando se aplican simplifican el cálculo, aplicar la regla del cociente y el producto no es práctico en funciones muy complejas, en este punto, optar por la diferenciación logarítmica es una mejor opción.
Método de resolución de Diferenciación Logarítmica
- Primero, tome el logaritmo natural en ambos lados de la ecuación dada.
- Aplique diferentes propiedades de log para romper la función y hacerla más fácil de resolver.
- Diferenciar la función aplicando reglas, como la regla de la string.
- Multiplique el RHS con la Función misma ya que estaba en el denominador del LHS.
Derivado de logₐx (para cualquier base positiva a≠1)
Se sabe que la diferenciación de logx es 1/x, pero esta es la diferenciación de logaritmo natural (es decir, base e), ¿es posible tener diferentes bases y su diferenciación también es posible? SÍ. Con la ayuda de 2 propiedades simples de log, se puede derivar.
Averigüemos la derivada de Log a x (donde a es cualquier número entero positivo a≠ 1),
d/dx(lnx)= 1/x
Cuando se cambian las bases, se pueden escribir como,
![]()
Por lo tanto, escribir log a x en la forma dada arriba y luego diferenciarlo dará,
![]()
Diferenciando ambos lados,
![Rendered by QuickLaTeX.com d/dx[log_ax]=d/dx[\frac{logx}{loga}]\\=\frac{1}{loga}d/dx[logx]\\=\frac{1}{xloga}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a5400032b7ee5bb2a411a4e36a68c418_l3.png)
Ejemplo 1: Encuentra la diferenciación para log 9 x
Responder:
d/dx[log 9 x]= d/dx[logx/log9]
Ejemplo 2: Diferenciar -5log 6 x
Responder:
Ejemplo 3: Diferenciar log 4 (x 2 +x)
Solución:
Como es claro, que la función dada es una función compuesta. Por lo tanto, la regla de la string es esencial para ser aplicada aquí.
y= logaritmo 4 (x 2 +x)
Supongamos que x 2 +x sea p(x)
p'(x)= 2x+1
Para la función de registro, llamémosla q(x)
q(x)= log 4 (x)
q'(x)=1/x.log4
y es la función completa que ahora se puede escribir como,
y= q(p(x))
y’= q'(p(x))× p'(x)
dy/dx=
Los ejemplos anteriores están relacionados con la diferenciación de log a x y también con la diferenciación de números compuestos.
Algunas propiedades básicas de Log
| Propiedad/Regla | Fórmula |
| Producto | ln(xy)= ln(x)+ ln(y) |
| Registro recíproco | ln(1/x)= -ln(x) |
| Registro de 1 | ln(1)= 0 |
| Registro de e | ln(e)= 1 |
| Registro de poder | ln(x) y = yln(x) |
| Cociente | ln(x/y)= ln(x)-ln(y) |
Ahora echemos un vistazo a algunos otros ejemplos basados en las propiedades del logaritmo.
Problemas de muestra
Pregunta 1: Diferenciar, ![]()
Solución:
diferenciando,
Suponga, 1-3x 3 = v(x)
Donde, v(x) también es una función de x, por lo tanto, también es necesario diferenciarla.
Pregunta 2: Diferenciar, h(x)= 5ln(x)
Solución:
d/dx[ln(x)]= 1/(x)
Por lo tanto, d/dx[h(x)] = h'(x)= d/dx[5/x]
h'(x)= 5/x
Pregunta 3: Diferenciar, y= ln(4+ 7x 5 )
Solución:
y’= d[y]/dx =d/dx[ln(4+7x 5 )]
dy/dx=
Pregunta 4: Diferenciar, y = cosx × cos3x × cos5x
Solución:
Agregue registro en ambos lados,
Logia= log{cosx × cos3x × cos5x}
Logia= log(cosx) × log(cos3x) × log(cos5x)
Diferenciando en ambos lados,
d/dx[logía]= d/dx[log(cosx) × log(cos3x) × log(cos5x)]
1/y × dy/dx = [(1/cosx) × d(cosx)/dx] + [1/cos3x × d(cos3x)/dx] + [1/cos5x × d(cos5x)/dx]
1/y × dy/dx = -senx/cosx -3sen3x/cos3x -5 sen5x/cos5x
dy/dx= y × {-tanx-3tan3x-5tan5x}
dy/dx= {cosx× cos3x × cos5x} × {-tanx -3tan3x -5tan5x}
Pregunta 5: ¿Cuál es el significado de Log de un número?
Responder:
Un Log o Logaritmos es la potencia a la que se debe elevar un número para obtener otro número. Por ejemplo, el logaritmo de base 10 para 1000 es 3, el logaritmo de base 10 de 10000 es 4, y así sucesivamente. El registro se usa para encontrar la asimetría en valores grandes y para mostrar el cambio porcentual de múltiples factores.
Pregunta 6: Diferenciar, ![]()
Responder:
Agregar registro en ambos lados,
Logy= (Senx)Log{log(x)}
Diferenciar con respecto a x en ambos lados,
1/a dy/dx=
dy/dx= y ×
dy/dx= logx senx
Pregunta 7: Explique en pasos para resolver la Diferenciación Logarítmica.
Responder:
Los pasos para resolver la diferenciación logarítmica son muy fáciles y cortos,
- Tome registro en ambos lados de la ecuación
- Utilice las propiedades de Log y simplifique RHS
- Diferencie ambos lados, aplique la regla de la string en RHS
- Pon el valor de la función en ambos lados
Pregunta 8: Diferenciar , ![]()
Responder:
Aplicar registro en ambos lados,
1/año dy/dx= d/dx {log(x+5) -log(x 3 + 3)}
1/año dy/dx = 1/(x+5) – 3x/(x 3 +3)
dy/dx= y [1/(x+5) – 3x/(x 3 +3)]
dy/dx=
Pregunta 9: Diferenciar , ![]()
Responder:
Tomando registro en ambos lados,
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com d/dx[log_9x]=d/dx[\frac{logx}{log9}]\\=\frac{1}{log9}d/dx[logx]\\=\frac{1}{xlog9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7855cfe82853ffba1db63d69f777d903_l3.png)
![Rendered by QuickLaTeX.com d/dx[-5log_6x]=-5[d/dx[\frac{logx}{log6}]]\\=-5[\frac{1}{log6}d/dx[logx]]\\=\frac{-5}{xlog9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-decff17cf29ad3e7c45ad72b3d1a9f7c_l3.png)
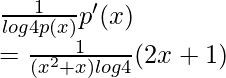
![Rendered by QuickLaTeX.com d/dx[f(x)]=d/dx[ log_2{(1-3x^3)}]\\=d/dx[ log_2{(v(x))}] \\=\frac{v'(x)}{log2{(v(x))}}\\= \frac{-9x^2}{log2(1-3x^3)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-327bf88eba4af65c91eb3fea6e37b7fd_l3.png)
![Rendered by QuickLaTeX.com \frac{d/dx[4+7x^5]}{4+7x^5}\\=\frac{35x^4}{4+7x^5}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8836b2c2b2a3ae41a2d951007bbe7f4b_l3.png)
![Rendered by QuickLaTeX.com logy=log [\frac{(x+3)(x^5-2)}{(x+10)(x^2+1)}]\\=log(x+3)+log(x^5-2)-log(x+10)-log(x^2+1) \\\frac{dy}{dx}\frac{1}{y}=\frac{1}{x+3}+\frac{5x^4}{x^5-2}-\frac{1}{x+10}-\frac{2x}{x^2+1} \\dy/dx=y[\frac{1}{x+3}+\frac{5x^4}{x^5-2}-\frac{1}{x+10}-\frac{2x}{x^2+1}] \\dy/dx= [\frac{(x+3)(x^5-2)}{(x+10)(x^2+1)}][\frac{1}{x+3}+\frac{5x^4}{x^5-2}-\frac{1}{x+10}-\frac{2x}{x^2+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0ac90f8ee22968cf6823ca7d280763d_l3.png)