Distancia chi-cuadrado en Python

El cálculo de la distancia chi-cuadrado es un método estadístico, generalmente mide la similitud entre 2 arrays de características. Dicha distancia se usa generalmente en muchas aplicaciones, como la recuperación de imágenes similares, la textura de imágenes, la extracción de características, etc. 
 

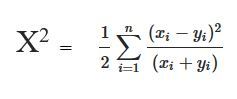
En este artículo, aprenderemos cómo calcular la distancia Chi-cuadrado usando Python. A continuación se dan 2 métodos diferentes para calcular la distancia Chi-cuadrado. Veamos ambos con ejemplos. 
Método #1: Cálculo de la distancia chi – cuadrada manualmente usando la fórmula anterior. 
 

# importing numpy library
import numpy as np
 
# Function to calculate Chi-distance
def chi2_distance(A, B):
 
    # compute the chi-squared distance using above formula
    chi = 0.5 * np.sum([((a - b) ** 2) / (a + b)
                      for (a, b) in zip(A, B)])
 
    return chi
 
# main function
if __name__== "__main__":
    a = [1, 2, 13, 5, 45, 23]
    b = [67, 90, 18, 79, 24, 98]
 
    result = chi2_distance(a, b)
    print("The Chi-square distance is :", result)

Input : a = [1, 2, 13, 5, 45, 23]
        b = [67, 90, 18, 79, 24, 98] 
Output : The Chi-square distance is : 133.55428601494035

Input : a = [91, 900, 78, 30, 602, 813]
        b = [57, 49, 36, 759, 234, 928]
Output :  The Chi-square distance is : 814.776999405035

  
 
Método #2: Usar el método scipy.stats.chisquare()
 

Sintaxis: scipy.stats.chisquare(f_obs, f_exp=None, ddof=0, axis=0) 
Parámetros: 
==> f_obs : array1 
==> f_exp : array2, opcional 
==> ddof(Delta grados de libertad – ajuste para valor p): int, opcional 
==> eje: int o Ninguno, opcional 
El valor predeterminado de ddof y eje es 0.
Devuelve: 
==> chisq: float o ndarray 
==> valor p de la prueba: float o ndarray 
 

# importing scipy
from scipy.stats import chisquare
 
k = [3, 4, 6, 2, 9, 5, 2]
print(chisquare(k))

Producción : 
 

Power_divergenceResult(statistic=8.516129032258064, pvalue=0.20267440425509237)