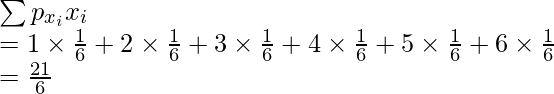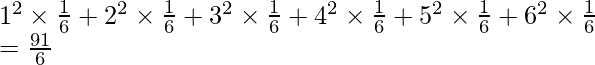Distribución de probabilidad

Distribución de probabilidad para una variable aleatoria muestra cómo se distribuyen las probabilidades para diferentes valores de la variable aleatoria. Cuando todos los valores de la variable aleatoria se alinean en un gráfico, los valores de sus probabilidades generan una forma. La distribución de probabilidad tiene varias propiedades (ejemplo: valor esperado y varianza) que se pueden medir.

En la distribución de probabilidad, el resultado de una variable aleatoria es incierto. Aquí, la observación del resultado se conoce como Realización. Es una función que mapea el espacio de muestra en un espacio de número real, conocido como espacio de estado. Pueden ser Discretos o Continuos.

Variables aleatorias

La variable aleatoria es un concepto importante en probabilidad y estadística. Necesitamos entenderlo intuitiva y matemáticamente para obtener una comprensión más profunda de las distribuciones de probabilidad que nos rodean en la vida cotidiana.

Es una función que asocia un número real con un evento.

A veces estamos interesados no solo en las probabilidades de los eventos en los experimentos sino también en algunos números asociados con el experimento. Aquí es cuando sentimos la necesidad de variables aleatorias.

Tomemos un ejemplo de los lanzamientos de monedas. Comenzaremos lanzando una moneda y lo averiguaremos. Usaremos H para significar ‘cara’ y T para ‘cruz’.

Así que ahora lanzamos nuestra moneda 5 veces y queremos responder algunas preguntas.

1. ¿Cuál es la probabilidad de obtener exactamente 3 caras?

2. ¿Cuál es la probabilidad de obtener menos de 4 caras?

3. ¿Cuál es la probabilidad de obtener más de 1 cara?

Entonces nuestra forma general de escribir sería:

· P(Probabilidad de obtener exactamente 3 caras cuando lanzamos una moneda 5 veces)

· P(Probabilidad de obtener menos de 4 caras cuando lanzamos una moneda 5 veces)

· P(Probabilidad de obtener más de 1 cara cuando lanzamos una moneda 5 veces)

En un escenario diferente, supongamos que estamos lanzando dos dados y nos interesa saber la probabilidad de obtener dos números tales que su suma sea 6.

Entonces, en ambos casos, las variables aleatorias vienen a nuestro rescate. Primero, definamos matemáticamente qué es una variable aleatoria.

Definición

Es una asignación de un valor (número) a cada resultado posible. En términos más matemáticos, es una función del espacio muestral Ω a los números reales. Podemos elegir nuestra variable aleatoria según nuestras necesidades.

Una variable aleatoria es una función de valor real cuyo dominio es el espacio muestral de un experimento aleatorio

Para hacer esto más intuitivo, consideremos el experimento de lanzar una moneda dos veces seguidas.

El espacio muestral del experimento es S = {HH, HT, TH, TT} . Definamos una variable aleatoria para contar eventos de cara o cruz según nuestra necesidad, sea X el número de caras obtenidas. Para cada resultado, sus valores son los siguientes:

X(HH) = 2, X (HT) = 1, X (TH) = 1, X (TT) = 0 .

Se puede definir más de una variable aleatoria en el mismo espacio muestral. Por ejemplo, sea Y el número de caras menos el número de cruces para cada resultado del espacio muestral S anterior.

Y(HH) = 2, Y (HT) = 0, Y (TH) = 0, Y (TT) = – 2

Por lo tanto, X e Y son dos variables aleatorias diferentes definidas en la misma muestra.

Nota: más de un evento puede asignarse al mismo valor de variable aleatoria.

Tipos de Variables Aleatorias en la Distribución de Probabilidad

Variables aleatorias discretas
Variables aleatorias continuas

Variables Aleatorias Discretas en Distribución de Probabilidad

Una variable aleatoria discreta solo puede tomar un número finito de valores. Para comprender mejor esto, veamos algunos ejemplos de variables aleatorias discretas:

X = {suma de los resultados cuando se lanzan dos dados}. Aquí, X solo puede tomar valores como {2, 3, 4, 5, 6….10, 11, 12}.
X = {Número de caras en 100 lanzamientos de moneda}. Aquí, X solo puede tomar valores enteros de [0,100].

Variable aleatoria continua en distribución de probabilidad

Una variable aleatoria continua puede tomar infinitos valores en un dominio continuo. Veamos un ejemplo de un juego de dardos.

Supongamos que tenemos un juego de dardos en el que lanzamos un dardo donde el dardo puede caer en cualquier lugar entre [-1,1] en el eje x. Entonces, si definimos nuestra variable aleatoria como la coordenada x de la posición del dardo, X puede tomar cualquier valor entre [-1,1]. Hay infinitos valores posibles que X puede tomar. (X = {0,1, 0,001, 0,01, 1,2, 2,112121… y así sucesivamente}.

Distribución de probabilidad de una variable aleatoria

Ahora viene la pregunta, ¿cómo describir el comportamiento de una variable aleatoria ?

Supongamos que nuestra variable aleatoria solo toma valores finitos, como x ₁ , x ₂ , x ₃ …. y xn _.Es decir, el rango de X es el conjunto de n valores {x ₁ , x ₂ , x ₃ …. y xn _} .

Así, el comportamiento de X se describe completamente dando probabilidades para todos los valores de la variable aleatoria X

Evento	Probabilidad
x1 _{_}	Pr(X = x ₁ )
x2 _{_}	Pr(X = _x2 )
x3 _{_}	Pr(X = _x3 )

La función de probabilidad de una variable aleatoria discreta X es la función p(x) que satisface

p(x) = Pr(X = x)

Veamos un ejemplo:

Pregunta: Sacamos dos cartas sucesivamente con reposición de un mazo bien barajado de 52 cartas. Encuentra la distribución de probabilidad de encontrar ases.

Responder:

Definamos una variable aleatoria “X”, que significa número de ases. Entonces, dado que solo estamos sacando dos cartas del mazo, X solo puede tomar tres valores: 0, 1 y 2. También sabemos que estamos sacando cartas con reemplazo, lo que significa que los dos sorteos pueden considerarse experimentos independientes.

P(X = 0) = P(ambas cartas no son ases)

= P(sin as) x P(sin as)

= $\frac{48}{52} \times \frac{48}{52} = \frac{144}{169}$

P(X = 1) = P(una de las cartas en as)

= P(sin as y luego as) + P(as y luego sin as)

= P(sin as) x P(as) + P(as) x P(sin as)

= $\frac{48}{52} \times \frac{4}{52} + \frac{4}{52} \times \frac{48}{52} = \frac{24}{169}$

P(X = 2) = P(Ambas cartas son ases)

= P(as) x P(as)

= $\frac{4}{52} \times \frac{4}{52} = \frac{1}{169}$

Ahora tenemos probabilidades para cada valor de variable aleatoria. Como es discreta, podemos hacer una tabla para representar esta distribución. La tabla se muestra a continuación.

X	0	1	2
PR	$\frac{144}{169}$	$\frac{24}{169}$	$\frac{1}{169}$

Expectativa (media) y varianza de una variable aleatoria

Supongamos que tenemos un experimento de probabilidad que estamos realizando y hemos definido alguna variable aleatoria (RV) de acuerdo con nuestras necesidades (como hicimos en algunos ejemplos anteriores). Ahora, cada vez que se realiza un experimento, nuestro RV toma un valor diferente. Pero queremos saber que si seguimos haciendo el experimento mil veces o un número infinito de veces, ¿cuál será el valor promedio de la variable aleatoria?

Expectativa

La media, el valor esperado o la expectativa de una variable aleatoria X se escribe como E( X ) o $\mu_{\textbf{X}}$ . Si observamos N valores aleatorios de X , entonces la media de los N valores será aproximadamente igual a E(X) para N grande.

Para una variable aleatoria X que toma valores x ₁ , x _2, x _{3 …} x _n con probabilidades p ₁ , p ₂ , p ₃ … p _n . La expectativa de X se define como,

$\sum_{i=1}^{N} x_{i}p_{i}$

es decir, es la media ponderada de todos los valores que puede tomar X, ponderada por la probabilidad de cada valor.

Para verlo de manera más intuitiva, echemos un vistazo a este gráfico a continuación,

Ahora, en la figura anterior, podemos ver que ambas variables aleatorias tienen casi la misma ‘media’, pero ¿eso significa que son iguales? No. Para describir completamente las propiedades/comportamiento de una variable aleatoria, necesitamos algo más, ¿no?

Necesitamos observar la dispersión de la distribución de probabilidad, una de ellas está concentrada, pero la otra está muy dispersa cerca de un solo valor. Entonces necesitamos una métrica para medir la dispersión en el gráfico.

Diferencia

En Estadística, hemos estudiado que la varianza es una medida de la dispersión o dispersión en los datos. Asimismo, la variabilidad o dispersión en los valores de una variable aleatoria puede medirse por varianza.

Para una variable aleatoria X que toma valores x ₁ , x ₂ , x ₃ … x _n con probabilidades p ₁ , p ₂ , p ₃ … p _n y la expectativa es E[X]

La varianza de X o Var( X ) se denota por, $E[X - u]^{2} = \sum (x_{i}-\mu)^{2}p_{x_{i}} = E[X^{2}] - (E[X])^ {2}$

Calculemos la media y la varianza de una distribución de probabilidad de variable aleatoria a través de un ejemplo:

Pregunta: Encuentre la varianza y la media del número obtenido en un lanzamiento de un dado no sesgado.

Responder:

Sabemos que el espacio muestral de este experimento es {1,2,3,4,5,6}

Definamos nuestra variable aleatoria X, que representa el número obtenido en un lanzamiento.

Entonces, las probabilidades de los valores que puede tomar nuestra variable aleatoria son,

P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = $\frac{1}{6}$

Por lo tanto, la distribución de probabilidad de la variable aleatoria es,

X 1 2 3 4 5 6

probabilidades $\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{6}$ $\frac{1}{6}$

E[X] = $\sum p_{x_{i}}x_{i} \\ \hspace{0.9cm} = 1 \times \frac{1}{6} + 2 \times \frac{1}{6} + 3 \times \ frac{1}{6} + 4 \times \frac{1}{6} + 5 \times \frac{1}{6} + 6 \times \frac{1}{6} \\ \hspace{0,9 cm } = \frac{21}{6}$

Además, E[X ² ] = $1^{2} \times \frac{1}{6} + 2^{2}\times\frac{1}{6} + 3^{2}\times\frac{1}{6} + 4^{2}\times\frac{1}{6} + 5^{2}\times\frac{1}{6} + 6^{2}\times\frac{1}{6} \\ \hspace{0.9cm} = \frac{91}{6} \\$

Así, Var(X) = E[X ² ] – (E[X]) ²

= $(\frac{91}{6}) - (\frac{21}{6})^{2} = \frac{91}{6} - \frac{441}{36} = \frac{35}{12}$

Entonces, por lo tanto, la media es $\frac{21}{6}$ y la varianza es $\frac{35}{12}$

Diferentes tipos de distribuciones de probabilidad

Hemos visto qué son las distribuciones de probabilidad, ahora veremos diferentes tipos de distribuciones de probabilidad. El tipo de distribución de probabilidad está determinado por el tipo de variable aleatoria. Hay dos tipos de distribuciones de probabilidad:

Distribuciones de probabilidad discretas para variables discretas
Funciones de densidad de probabilidad para variables continuas

Estudiaremos en detalle dos tipos de distribuciones de probabilidad discretas, otras están fuera del alcance de la clase 12.

Distribuciones de probabilidad discretas

Las funciones de probabilidad discreta asumen un número discreto de valores. Por ejemplo, los lanzamientos de monedas y el conteo de eventos son funciones discretas. Estas son distribuciones discretas porque no hay valores intermedios. Podemos tener cara o cruz en un lanzamiento de moneda.

Para funciones de distribución de probabilidad discretas, cada valor posible tiene una probabilidad distinta de cero. Además, las probabilidades de todos los valores de las variables aleatorias deben sumar uno. Por ejemplo, la probabilidad de sacar un número específico en un dado es 1/6. La probabilidad total para los seis valores es igual a uno. Cuando lanzamos un dado, solo obtenemos cualquiera de estos valores.

Pruebas de Bernoulli y distribuciones binomiales

Muchos experimentos solo tienen uno de dos resultados. Por ejemplo, una moneda lanzada al aire muestra ‘cara’ o ‘cruz’, un artículo fabricado puede ser ‘defectuoso’ o ‘no defectuoso’. En estos casos, podemos llamar a uno de estos resultados “éxito” ya otro “fracaso”. Digamos que en el experimento de lanzar una moneda, si la aparición de cara se considera un éxito, entonces la aparición de cruz es un fracaso.

Cada vez que lanzamos una moneda o tiramos un dado o realizamos cualquier otro experimento, lo llamamos prueba. Ahora sabemos que en nuestros experimentos de prueba de lanzamiento de monedas, el resultado de cualquier prueba es independiente del resultado de cualquier otra prueba. En cada uno de estos ensayos, la probabilidad de éxito o fracaso permanece constante. Estos ensayos independientes que tienen solo dos resultados, generalmente denominados «éxito» o «fracaso», se denominan ensayos de Bernoulli.

Definición:

Las pruebas del experimento aleatorio se conocen como pruebas de Bernoulli, si cumplen las siguientes condiciones:

Se requiere un número finito de ensayos.

Todos los ensayos deben ser independientes.

Toda prueba tiene dos resultados: éxito o fracaso.

La probabilidad de éxito sigue siendo la misma en cada ensayo.

Tomemos el ejemplo del experimento en el que lanzamos un dado, lanzar un dado 50 veces puede considerarse como un caso de 50 intentos de Bernoulli, donde el resultado de cada intento es un éxito (supongamos que obtener un número par es un éxito) o un fracaso ( de manera similar, obtener un número impar es fallar) y la probabilidad de éxito (p) es la misma para los 50 lanzamientos. Obviamente, los lanzamientos sucesivos del dado son ensayos independientes. Si el dado es justo y tiene seis números del 1 al 6 escritos en seis caras, entonces p = 1/2 y q = 1 – p = 1/2 = probabilidad de fracaso.

Pregunta: Una urna contiene 8 bolas rojas y 10 bolas negras. Sacamos seis bolas de la urna sucesivamente. Tienes que decir si las pruebas de sacar bolas son o no pruebas de Bernoulli cuando después de cada sorteo, la bola extraída es:

sustituido
no reemplazado en urna.

Responder:

Sabemos que el número de ensayos es finito. Cuando se extrae con reemplazo, la probabilidad de éxito (por ejemplo, bola roja) es p = 8/18, que será la misma para los seis intentos. Entonces, el sorteo de bolas con reemplazos son pruebas de Bernoulli.

Si el sorteo se realiza sin reemplazo, la probabilidad de éxito (es decir, bola roja) en el primer intento es 8/18, en el segundo intento es 7/17 si la primera bola extraída es roja o 10/18 si la primera bola extraída es negra. y así. Claramente, las probabilidades de éxito no son las mismas para todas las pruebas. Por lo tanto, las pruebas no son pruebas de Bernoulli.

Distribución binomial

Es una variable aleatoria que representa el número de éxitos en “N” ensayos independientes sucesivos del experimento de Bernoulli. Se utiliza en una gran cantidad de casos, como incluir el número de caras en lanzamientos de moneda «N», y así sucesivamente.

Sean P y Q el éxito y el fracaso en el juicio de Bernoulli. Supongamos que estamos interesados en encontrar diferentes formas en las que tenemos 1 éxito en las seis pruebas.

Claramente, hay seis casos disponibles como se enumeran a continuación:

PQQQQQ, QPQQQQ, QQPQQQ, QQQPQQ, QQQQPQ, QQQQQP

Asimismo, 2 éxitos y 4 fracasos mostrarán $\frac{6!}{4! 2!}$ combinaciones. Tantas combinaciones son muy difíciles de enumerar. De ahora en adelante, calcular las probabilidades de 0, 1, 2,…, n número de éxitos puede ser largo y llevar mucho tiempo. Para evitar un cálculo tan extenso junto con una lista de todos los casos posibles, para las probabilidades del número de éxitos en las pruebas de n-Bernoulli, se elabora una fórmula:

Si Y es una variable aleatoria binomial, denotamos esta Y∼ Bin(n, p), donde p es la probabilidad de éxito en un intento dado, q es la probabilidad de fracaso, Sea ‘n’ el número total de intentos y ‘x’ sea el número de éxitos. Una variable aleatoria binomial tiene las siguientes propiedades:

P(Y) = norte C _x q ⁿ^–x pag ^x

Ahora la función de probabilidad P(Y) se conoce como la función de probabilidad de la distribución binomial.

Pregunta: Cuando se lanza una moneda justa 10 veces, la probabilidad de:

exactamente seis cabezas
al menos seis cabezas

Respuesta :

Cada moneda lanzada al aire puede considerarse como el juicio de Bernoulli. Suponga que X es el número de cabezas en este experimento:

Ya sabemos, n = 10

pag = 1/2

Entonces, P(X = x) = ⁿ C _x p ^n-x (1-p) ^x , x= 0,1,2,3,….n

P(X = x) = ¹⁰ C _x p ^10-x (1-p) ^x

Cuando x = 6,

(i) P(x = 6) = ¹⁰ C ₆ p ⁴ (1-p) ⁶

= $\frac{10!}{6!4!}(\frac{1}{2})^{6}(\frac{1}{2})^{4}\\ \hspace{0.4cm} = \frac{7\times8\times9\times10}{2\times3\times4}\times\frac{1}{64}\times\frac{1}{16} \\ \hspace{0.4cm} = \frac{105}{512}$

(ii) P(al menos 6 caras) = P(X >= 6) = P(X = 6) + P(X=7) + P(X=8)+ P(X=9) + P(X =10)

= ¹⁰ C ₆ p ⁴ (1-p) ⁶ + ¹⁰ C ₇ p ³ (1-p) ⁷ + ¹⁰ C ₈ p ² (1-p) ⁸ + ¹⁰ C ₉ p ¹ (1-p) ⁹ + ¹⁰ C ₁₀ (1-p) ¹⁰ =

$\frac{10!}{6!4!}(\frac{1}{2})^{10} + \frac{10!}{7!3!}(\frac{1}{2})^{10} + \frac{10!}{8!2!}(\frac{1}{2})^{10} + \frac{10!}{9!1!}(\frac{1}{2})^{10} + \frac{10!}{10!}(\frac{1}{2})^{10}\\ \hspace{0.5cm} = (\frac{10!}{6!4!} + \frac{10!}{7!3!}+ \frac{10!}{8!2!} + \frac{10!}{9!1!}+ \frac{10!}{10!})(\frac{1}{2})^{10} \\ \hspace{0.5cm} = \frac{193}{512}$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Variables aleatorias

Definición

Tipos de Variables Aleatorias en la Distribución de Probabilidad

Variables Aleatorias Discretas en Distribución de Probabilidad

Variable aleatoria continua en distribución de probabilidad

Distribución de probabilidad de una variable aleatoria

Expectativa (media) y varianza de una variable aleatoria

Expectativa

Diferencia

Diferentes tipos de distribuciones de probabilidad

Distribuciones de probabilidad discretas

Pruebas de Bernoulli y distribuciones binomiales

Distribución binomial

Deja una respuesta Cancelar la respuesta