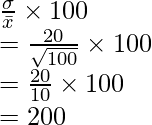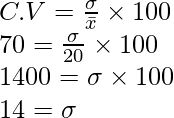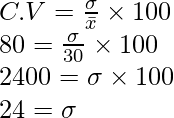Distribuciones de frecuencia

La distribución de frecuencias ocurre en todas partes de nuestras vidas. Departamento meteorológico, científicos de datos, ingenieros civiles, casi todas las profesiones utilizan distribuciones de frecuencia en sus profesiones. Estas distribuciones nos permiten obtener información de cualquier dato, ver las tendencias y predecir los próximos valores o la dirección en la que irán los datos. Hay dos tipos de distribuciones de frecuencia: agrupadas y no agrupadas. Su uso depende de los datos sobre los que estemos trabajando. Su análisis es una parte muy importante de la probabilidad y la estadística. Veamos estos conceptos en detalle.

Distribuciones de frecuencia

Las distribuciones de frecuencia nos dicen cómo se distribuyen las frecuencias sobre los valores. Eso es cuántos valores se encuentran entre diferentes intervalos. Nos dan una idea sobre el rango donde caen la mayoría de los valores y los rangos donde los valores son escasos.

Una distribución de frecuencia es una descripción general de todos los valores de alguna variable y la cantidad de veces que ocurren.

Las distribuciones de frecuencia son de tipos:

Distribuciones de frecuencia agrupadas : los valores se dividen entre diferentes intervalos y luego se cuentan sus frecuencias.
Distribuciones de frecuencia no agrupadas: se mencionan todos los valores distintos de la variable y se cuentan sus frecuencias.

Pregunta: Digamos que tenemos datos de los goles marcados por un equipo en 10 partidos diferentes.

1, 0, 0, 3, 2, 0, 2, 3, 1, 1

Dibuja una tabla de frecuencias para representar estos datos.

Solución:

Dado que hay menos número de valores distintos. No tenemos que agrupar los datos. Solo podemos contar los distintos valores y su frecuencia.

Número de goles Frecuencia

0 3

1 3

2 2

3 2

Total 10

Esta tabla de frecuencias también se puede representar en forma de gráfico de barras.

Una distribución de frecuencia también se puede representar mediante una línea curva. La figura que se muestra a continuación representa la línea de curva para el problema anterior.

Del mismo modo, si hay muchos valores distintos, podemos agruparlos y hacer distribuciones de frecuencia agrupadas como en el caso anterior.

Distribución de frecuencia acumulada

La frecuencia acumulada se define como la suma de todas las frecuencias en los valores o intervalos anteriores hasta el actual. Las distribuciones de frecuencia que representan las distribuciones de frecuencia utilizando frecuencias acumulativas se denominan distribuciones de frecuencia acumulativas. Hay dos tipos de distribuciones de frecuencia acumulada:

Menos que tipo: sumamos todas las frecuencias antes del intervalo actual.
Más que tipo: sumamos todas las frecuencias después del intervalo actual.

Veamos cómo representar una distribución de frecuencia acumulada a través de un ejemplo,

Pregunta 1: La siguiente tabla muestra los valores de las carreras anotadas por Virat Kohli en los últimos 25 partidos de T-20. Representar los datos en forma de distribución de frecuencia acumulada menor que tipo:

45	34	50	75	22
56	63	70	49	33
0	8	14	39	86
92	88	70	56	50
57	45	42	12	39

Solución:

Dado que hay muchos valores distintos, lo expresaremos en forma de distribuciones agrupadas con intervalos como 0-10, 10-20, etc. Primero representemos los datos en forma de distribución de frecuencia agrupada.

Carreras Frecuencia

0-10 2

10-20 2

20-30 1

30-40 4

40-50 4

50-60 5

60-70 1

70-80 2

80-90 2

90-100 1

Ahora convertiremos esta distribución de frecuencias en una distribución de frecuencias acumulada sumando los valores del intervalo actual y todos los intervalos anteriores.

Carreras Frecuencia

0-10 2

10-20 4

20-30 5

30-40 9

40-50 13

50-60 18

60-70 19

70-80 21

80-90 23

90-100 25

Esta tabla representa la distribución de frecuencia acumulada.

Pregunta 2: Representa la tabla de distribución de frecuencia acumulada anterior en forma de curva de línea de distribución de frecuencia acumulada.

Solución:

Para trazar la curva de línea de la tabla anterior, use el punto medio de cada intervalo y el valor correspondiente.

Coeficiente de variación

Sabemos cómo medir la dispersión de una serie. Podemos usar la media y la desviación estándar para describir la dispersión en los valores. Pero a veces, comparar las dos series o distribuciones de frecuencia se vuelve un poco difícil, ya que a veces ambas tienen unidades diferentes.

Por ejemplo: Digamos que tenemos dos series, sobre las alturas de los alumnos de una clase. Ahora una serie mide la altura en cm y la otra en metros. Idealmente, ambos deberían tener la misma dispersión, pero los métodos de medición de la dispersión dependen de las unidades en las que estamos midiendo. Esto hace que tales comparaciones sean difíciles. Para tratar con tales problemas, definimos el Coeficiente de Variación.

El coeficiente de variación se define como,

$\frac{\sigma}{\bar{x}} \times 100$

Aquí, $\sigma$ y $\bar{x}$ son la desviación estándar y la media de la serie.

Se dice que la serie que tiene mayor CV es más variable que la otra. Se dice que la serie que tiene menor CV es más consistente que la otra.

Comparación de dos distribuciones de frecuencia con la misma media

Tenemos dos distribuciones de frecuencia. Digamos que $\sigma_{1}$ y $\bar{x}_1$ son la desviación estándar y la media de la primera serie y $\sigma_2$ y $\bar{x}_2$ son la desviación estándar y la media de la segunda serie.

CV de la primera serie = $\frac{\sigma_1}{\bar{x}_1} \times 100$

CV de la segunda serie = $\frac{\sigma_2}{\bar{x}_2} \times 100$

Se nos da que ambas series tienen la misma media, es decir

$\bar{x}_2 = \bar{x}_1 = \bar{x}$

Entonces, ahora el CV para ambas series es,

CV de la primera serie = $\frac{\sigma_1}{\bar{x}} \times 100$

CV de la segunda serie = $\frac{\sigma_2}{\bar{x}} \times 100$

Observe que ahora ambas series se pueden comparar solo con el valor de la desviación estándar. Por tanto, podemos decir que para dos series con la misma media, la serie con mayor desviación puede considerarse más variable que la otra.

Veamos algunos ejemplos de estos conceptos:

Problemas de muestra

Pregunta 1: Supongamos que tenemos una serie, con una media de 20 y una varianza de 100. Averigüe el coeficiente de variación.

Solución:

Conocemos la fórmula del coeficiente de variación,

$\frac{\sigma}{\bar{x}} \times 100$

Dada la media $\bar{x}$ = 20 y la varianza $\sigma^2$ = 100.

Sustituyendo los valores en la fórmula,

$\frac{\sigma}{\bar{x}} \times 100 \\ = \frac{20}{\sqrt{100}} \times 100 \\ = \frac{20}{10} \times 100 \\ = 200$

Pregunta 2: Dadas dos series con Coeficiente de Variación 70 y 80. Las medias son 20 y 30. Encuentra los valores de desviación estándar para ambas series.

Solución:

En esta pregunta necesitamos aplicar la fórmula para CV y sustituir los valores dados.

Desviación estándar de la primera serie.

$C.V = \frac{\sigma}{\bar{x}} \times 100 \\ 70 = \frac{\sigma}{20} \times 100 \\ 1400 = \sigma \times 100 \\ 14 = \sigma$

Por lo tanto, la desviación estándar de la primera serie = 14.

Desviación estándar de la segunda serie.

$C.V = \frac{\sigma}{\bar{x}} \times 100 \\ 80 = \frac{\sigma}{30} \times 100 \\ 2400 = \sigma \times 100 \\ 24 = \sigma$

Por lo tanto, la desviación estándar de la primera serie = 24.

Pregunta 3: Dibuje la tabla de distribución de frecuencias y la curva de distribución de frecuencias para los siguientes datos:

2, 3, 1, 4, 2, 2, 3, 1, 4, 4, 4, 2, 2, 2

Solución:

Dado que solo hay muy pocos valores distintos en la serie, trazaremos la distribución de frecuencias no agrupadas.

Valor Frecuencia

1 2

2 6

3 2

4 4

Total 14

La siguiente figura representa la curva de línea para la tabla dada.

Pregunta 4: La siguiente tabla muestra los valores de temperatura registrados en Hyderabad durante 25 días en verano. Representar los datos en forma de distribución de frecuencia acumulada menor que tipo:

37	34	36	27	22
25	25	24	26	28
30	31	29	28	30
32	31	28	27	30
30	32	35	34	29

Solución:

Como hay tantos valores distintos aquí, usaremos una distribución de frecuencia agrupada. Digamos que los intervalos son 20-25, 25-30, 30-35. La tabla de distribución de frecuencias se puede hacer contando el número de valores que se encuentran en estos intervalos.

La temperatura Número de días

20-25 2

25-30 10

30-35 13

Esta es la tabla de distribución de frecuencias agrupadas. Se puede convertir en distribución de frecuencia acumulada sumando los valores anteriores.

La temperatura Número de días

20-25 2

25-30 12

30-35 25

La tabla anterior es la distribución de frecuencia acumulada de los datos anteriores. Ahora representemos esto en forma de curva de línea para la distribución de frecuencia acumulada.

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA