El autómata finito determinista (DFA) se puede utilizar para comprobar si un número «num» es divisible por «k» o no. Si el número no es divisible, el resto también se puede obtener mediante DFA.
Consideramos la representación binaria de ‘num’ y construimos un DFA con k estados. El DFA tiene una función de transición para 0 y 1. Una vez que se crea el DFA, procesamos ‘num’ sobre el DFA para obtener el resto.
Veamos un ejemplo. Supongamos que queremos comprobar si un número dado ‘num’ es divisible por 3 o no. Cualquier número se puede escribir en la forma: num = 3*a + b donde ‘a’ es el cociente y ‘b’ es el resto.
Para 3, puede haber 3 estados en DFA, cada uno correspondiente al resto 0, 1 y 2. Y cada estado puede tener dos transiciones correspondientes a 0 y 1 (considerando la representación binaria de ‘num’ dado).
La función de transición F(p, x) = q dice que al leer el alfabeto x, pasamos del estado p al estado q. Llamemos a los estados como 0, 1 y 2. El estado inicial siempre será 0. El estado final indica el resto. Si el estado final es 0, el número es divisible.
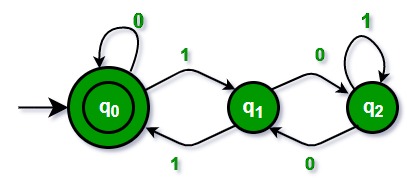
En el diagrama anterior, el estado de doble círculo es el estado final.
1. Cuando estamos en el estado 0 y leemos 0, nos quedamos en el estado 0.
2. Cuando estamos en el estado 0 y leemos 1, pasamos al estado 1, ¿por qué? El número así formado (1) en decimal da resto 1.
3. Cuando estamos en el estado 1 y leemos 0, pasamos al estado 2, ¿por qué? El número así formado (10) en decimal da resto 2.
4. Cuando estamos en el estado 1 y leemos 1, pasamos al estado 0, ¿por qué? El número así formado (11) en decimal da resto 0.
5. Cuando estamos en el estado 2 y leemos 0, pasamos al estado 1, ¿por qué? El número así formado (100) en decimal da resto 1.
6. Cuando estamos en el estado 2 y leemos 1, permanecemos en el estado 2, ¿por qué? El número así formado (101) en decimal da el resto 2.
La tabla de transición se parece a la siguiente:
state 0 1 _____________ 0 0 1 1 2 0 2 1 2
Comprobemos si 6 es divisible por 3.
La representación binaria de 6 es 110
estado = 0
1. estado=0, leemos 1, nuevo estado=1
2. estado=1, leemos 1, nuevo estado=0
3. estado=0, leemos 0, nuevo estado= 0
Como el estado final es 0, el número es divisible por 3.
Tomemos otro número de ejemplo como 4
estado=0
1. estado=0, leemos 1, nuevo estado=1
2. estado=1, leemos 0, nuevo estado=2
3. estado=2, leemos 0, nuevo estado=1
Dado que el estado final no es 0, el número no es divisible por 3. El resto es 1.
Tenga en cuenta que el estado final da el resto.
Podemos extender la solución anterior para cualquier valor de k. Para un valor k, los estados serían 0, 1,…. , k-1. ¿Cómo calcular la transición si el equivalente decimal de los bits binarios vistos hasta ahora cruza el rango k? Si estamos en el estado p, hemos leído p (en decimal). Ahora leemos 0, el nuevo número de lectura se convierte en 2*p. Si leemos 1, el nuevo número de lectura se convierte en 2*p+1. El nuevo estado se puede obtener restando k de estos valores (2p o 2p+1) donde 0 <= p < k.
Basado en el enfoque anterior, el siguiente es el código de trabajo:
C++
#include <bits/stdc++.h>
using namespace std;
// Function to build DFA for divisor k
void preprocess(int k, int Table[][2])
{
int trans0, trans1;
// The following loop calculates the
// two transitions for each state,
// starting from state 0
for (int state = 0; state < k; ++state)
{
// Calculate next state for bit 0
trans0 = state << 1;
Table[state][0] = (trans0 < k) ?
trans0 : trans0 - k;
// Calculate next state for bit 1
trans1 = (state << 1) + 1;
Table[state][1] = (trans1 < k) ?
trans1 : trans1 - k;
}
}
// A recursive utility function that
// takes a 'num' and DFA (transition
// table) as input and process 'num'
// bit by bit over DFA
void isDivisibleUtil(int num, int* state,
int Table[][2])
{
// process "num" bit by bit
// from MSB to LSB
if (num != 0)
{
isDivisibleUtil(num >> 1, state, Table);
*state = Table[*state][num & 1];
}
}
// The main function that divides 'num'
// by k and returns the remainder
int isDivisible (int num, int k)
{
// Allocate memory for transition table.
// The table will have k*2 entries
int (*Table)[2] = (int (*)[2])malloc(k*sizeof(*Table));
// Fill the transition table
preprocess(k, Table);
// Process ‘num’ over DFA and
// get the remainder
int state = 0;
isDivisibleUtil(num, &state, Table);
// Note that the final value
// of state is the remainder
return state;
}
// Driver Code
int main()
{
int num = 47; // Number to be divided
int k = 5; // Divisor
int remainder = isDivisible (num, k);
if (remainder == 0)
cout << "Divisible\n";
else
cout << "Not Divisible: Remainder is "
<< remainder;
return 0;
}
// This is code is contributed by rathbhupendra
C
#include <stdio.h>
#include <stdlib.h>
// Function to build DFA for divisor k
void preprocess(int k, int Table[][2])
{
int trans0, trans1;
// The following loop calculates the two transitions for each state,
// starting from state 0
for (int state=0; state<k; ++state)
{
// Calculate next state for bit 0
trans0 = state<<1;
Table[state][0] = (trans0 < k)? trans0: trans0-k;
// Calculate next state for bit 1
trans1 = (state<<1) + 1;
Table[state][1] = (trans1 < k)? trans1: trans1-k;
}
}
// A recursive utility function that takes a 'num' and DFA (transition
// table) as input and process 'num' bit by bit over DFA
void isDivisibleUtil(int num, int* state, int Table[][2])
{
// process "num" bit by bit from MSB to LSB
if (num != 0)
{
isDivisibleUtil(num>>1, state, Table);
*state = Table[*state][num&1];
}
}
// The main function that divides 'num' by k and returns the remainder
int isDivisible (int num, int k)
{
// Allocate memory for transition table. The table will have k*2 entries
int (*Table)[2] = (int (*)[2])malloc(k*sizeof(*Table));
// Fill the transition table
preprocess(k, Table);
// Process ‘num’ over DFA and get the remainder
int state = 0;
isDivisibleUtil(num, &state, Table);
// Note that the final value of state is the remainder
return state;
}
// Driver program to test above functions
int main()
{
int num = 47; // Number to be divided
int k = 5; // Divisor
int remainder = isDivisible (num, k);
if (remainder == 0)
printf("Divisible\n");
else
printf("Not Divisible: Remainder is %d\n", remainder);
return 0;
}
Javascript
// JavaScript program to implement the approach
// Function to build DFA for divisor k
function preprocess(k, Table)
{
let trans0, trans1;
// The following loop calculates the
// two transitions for each state,
// starting from state 0
for (let state = 0; state < k; ++state)
{
// Calculate next state for bit 0
trans0 = state << 1;
Table[state][0] = (trans0 < k) ?
trans0 : trans0 - k;
// Calculate next state for bit 1
trans1 = (state << 1) + 1;
Table[state][1] = (trans1 < k) ?
trans1 : trans1 - k;
}
}
// A recursive utility function that
// takes a 'num' and DFA (transition
// table) as input and process 'num'
// bit by bit over DFA
function isDivisibleUtil(num, state, Table)
{
// process "num" bit by bit
// from MSB to LSB
if (num != 0)
{
state = isDivisibleUtil(num >> 1, state, Table);
state = Table[state][num & 1];
}
return state;
}
// The main function that divides 'num'
// by k and returns the remainder
function isDivisible (num, k)
{
// Allocate memory for transition table.
// The table will have k*2 entries
Table = new Array(k);
for (let i = 0; i < k; i++)
Table[i] = [0, 0];
// Fill the transition table
preprocess(k, Table);
// Process ‘num’ over DFA and
// get the remainder
let state = 0;
state = isDivisibleUtil(num, state, Table);
// Note that the final value
// of state is the remainder
return state;
}
// Driver Code
let num = 47; // Number to be divided
let k = 5; // Divisor
let remainder = isDivisible (num, k);
if (remainder == 0)
console.log("Divisible");
else
console.log("Not Divisible: Remainder is " + remainder);
// This is code contributed by phasing17
Python3
# Python3 program to implement the approach
# Function to build DFA for divisor k
def preprocess(k, Table):
# The following loop calculates the
# two transitions for each state,
# starting from state 0
for state in range(k):
# Calculate next state for bit 0
trans0 = state << 1
if (trans0 < k):
Table[state][0] = trans0
else:
Table[state][0] = trans0 - k
# Calculate next state for bit 1
trans1 = (state << 1) + 1
if trans1 < k:
Table[state][1] = trans1
else:
Table[state][1] = trans1 - k
# A recursive utility function that
# takes a 'num' and DFA (transition
# table) as input and process 'num'
# bit by bit over DFA
def isDivisibleUtil(num, state, Table):
# process "num" bit by bit
# from MSB to LSB
if (num != 0):
state = isDivisibleUtil(num >> 1, state, Table)
state = Table[state][num & 1]
return state
# The main function that divides 'num'
# by k and returns the remainder
def isDivisible(num, k):
# Allocate memory for transition table.
# The table will have k*2 entries
Table = [None for i in range(k)]
for i in range(k):
Table[i] = [0, 0]
# Fill the transition table
preprocess(k, Table)
# Process ‘num’ over DFA and
# get the remainder
state = 0
state = isDivisibleUtil(num, state, Table)
# Note that the final value
# of state is the remainder
return state
# Driver Code
num = 47 # Number to be divided
k = 5 # Divisor
remainder = isDivisible(num, k)
if (remainder == 0):
print("Divisible")
else:
print("Not Divisible: Remainder is", remainder)
# This is code contributed by phasing17
Producción:
Not Divisible: Remainder is 2
Complejidad de tiempo: O(k)
La división basada en DFA puede ser útil si tenemos una secuencia binaria como entrada y queremos verificar la divisibilidad del valor decimal de la secuencia en cualquier momento.
Artículos relacionados:
Verificar la divisibilidad en un flujo binario
Verificar si un flujo es múltiplo de 3
Este artículo fue compilado por Aashish Barnwal y revisado por el equipo de GeeksforGeeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA