Ecuación de una Línea en 3D

Todos conocemos la ecuación muy popular de la línea recta Y = m. X + C que es una línea recta en un plano. Pero aquí vamos a discutir la ecuación de una línea recta en un espacio tridimensional. Una Línea Recta se caracteriza de forma única si pasa por los dos puntos únicos o si pasa por un punto único en una dirección definida. En la geometría tridimensional, las líneas (líneas rectas) se representan generalmente en las dos formas Forma cartesiana y Forma vectorial. Aquí vamos a discutir la forma de dos puntos de una línea recta en 3 dimensiones utilizando tanto la forma cartesiana como la vectorial.

Ecuación de una Línea Recta en Forma Cartesiana

Para escribir la ecuación de una línea recta en forma cartesiana necesitamos las coordenadas de un mínimo de dos puntos por donde pasa la línea recta. Digamos que (x ₁ , y ₁ , z ₁ ) y (x ₂ , y ₂ , z ₂ ) son las coordenadas de posición de los dos puntos fijos en el espacio tridimensional a través del cual pasa la línea.

Ahora para obtener la ecuación tenemos que seguir estos tres pasos:

• Paso 1: encuentre las DR (relaciones de dirección) tomando la diferencia de las coordenadas de posición correspondientes de los dos puntos dados. l = (x ₂ – x ₁ ), m = (y ₂ – y ₁ ), n = (z ₂ – z ₁ ); Aquí l, m, n son los DR.
• Paso 2: Elija cualquiera de los dos puntos dados, digamos, elegimos (x ₁ , y ₁ , z ₁ ).
• Paso 3: Escriba la ecuación requerida de la línea recta que pasa por los puntos (x ₁ , y ₁ , z ₁ ) y (x ₂ , y ₂ , z ₂ ). L : (x – x ₁ )/l = (y – y ₁ )/m = (z – z ₁ )/n

Donde (x, y, z) son las coordenadas de posición de cualquier punto variable que se encuentre en la línea recta.

Ejemplo 1: si una línea recta pasa por los dos puntos fijos en el tridimensional cuyas coordenadas de posición son P (2, 3, 5) y Q (4, 6, 12), entonces su ecuación cartesiana usando la forma de dos puntos es dado por

Solución:

l = (4 – 2), m = (6 – 3), n = (12 – 5)

l = 2, m = 3, n = 7

Elección del punto P (2, 3, 5)

La ecuación requerida de la línea.

L : (x – 2) / 2 = (y – 3) / 3 = (z – 5) / 7

Ejemplo 2: si una línea recta pasa por los dos puntos fijos en el tridimensional cuyas coordenadas de posición son A (2, -1, 3) y B (4, 2, 1), entonces su ecuación cartesiana usando los dos puntos la forma esta dada por

Solución:

l = (4 – 2), m = (2 – (-1)), n = (1 – 3)

l = 2, m = 3, n = -2

Elegir el punto A (2, -1, 3)

La ecuación requerida de la línea.

L : (x – 2) / 2 = (y + 1) / 3 = (z – 3) / -2 o

L : (x – 2) / 2 = (y + 1) / 3 = (3 – z) / 2

Ejemplo 3: si una línea recta pasa por dos puntos fijos en el tridimensional cuyas coordenadas de posición son X (2, 3, 4) e Y (5, 3, 10), entonces su ecuación cartesiana usando la forma de dos puntos es dado por

Solución:

l = (5 – 2), m = (3 – 3), n = (10 – 4)

l = 3, m = 0, n = 6

Elegir el punto X (2, 3, 4)

La ecuación requerida de la línea.

L : (x – 2) / 3 = (y – 3) / 0 = (z – 4) / 6 o

L : (x – 2) / 1 = (y – 3) / 0 = (z – 4) / 2

Ecuación de una línea recta en forma vectorial

Para escribir la ecuación de una línea recta en forma vectorial necesitamos los vectores de posición de un mínimo de dos puntos por donde pasa la línea recta. Digamos   y   son los vectores de posición de los dos puntos fijos en el espacio tridimensional por donde pasa la línea.

Ahora para obtener la ecuación tenemos que seguir estos tres pasos:

• Paso 1: encuentre un vector paralelo a la línea recta restando los vectores de posición correspondientes de los dos puntos dados. 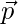 = ( 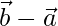); Aquí  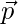 está el vector paralelo a la línea recta.
• Paso 2: Elija el vector de posición de cualquiera de los dos puntos dados, digamos que elegimos . 
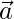
• Paso 3: Escriba la ecuación requerida de la línea recta que pasa por los puntos cuyos vectores de posición son y . L :   =   + t . o   =   + t. ( )      

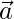
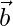
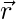
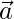
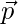
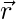
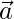
Donde   es el vector de posición de cualquier punto variable que se encuentra en la línea recta y t es el parámetro cuyo valor se usa para ubicar cualquier punto en la línea de manera única.

Ejemplo 1: Si una línea recta pasa por los dos puntos fijos en 3 dimensiones cuyos vectores de posición son (2 i + 3 j + 5 k) y (4 i + 6 j + 12 k) entonces su ecuación vectorial usando el la forma de dos puntos viene dada por

Solución:

 = (4 yo + 6 j + 12 k ) – (2 yo + 3 j + 5 k )

 = (2 yo + 3 j + 7 k ) ; Aquí   hay un vector paralelo a la línea recta.

Elegir el vector de posición (2 i + 3 j + 5 k )

La ecuación requerida de la línea recta.

L :   = (2 yo + 3 j + 5 k ) + t . (2 i + 3 j + 7 k )

Ejemplo 2: si una línea recta pasa a través de dos puntos fijos en el espacio tridimensional cuyas coordenadas de posición son (3, 4, -7) y (1, -1, 6), entonces su ecuación vectorial usando los dos puntos la forma esta dada por

Solución:

Los vectores de posición de los puntos dados serán (3 i + 4 j – 7 k) y (i – j + 6 k)

 = (3 i + 4 j – 7 k) – (i – j + 6 k)

 = (2 i + 5 j – 13 k) ; Aquí   hay un vector paralelo a la línea recta.

Elección del vector de posición (i – j + 6 k)

La ecuación requerida de la línea recta.

L :   = (yo – j + 6 k) + t . (2 i + 5 j – 13 k)

Ejemplo 3: Si una línea recta pasa por los dos puntos fijos en el tridimensional cuyos vectores de posición son (5 i + 3 j + 7 k) y (2 i + j – 3 k) entonces su ecuación vectorial usando los dos -la forma puntual está dada por

Solución:

 = (5 i + 3 j + 7 k) – (2 i + j – 3 k)

 = (3 yo + 2 j + 10 k) ; Aquí   hay un vector paralelo a la línea recta.

Elegir el vector de posición (2 i + j – 3 k)

La ecuación requerida de la línea recta.

L :   = (2 yo + j – 3 k) + t . (2 i + 3 j + 7 k)