Ecuación del círculo desde el centro y el radio.

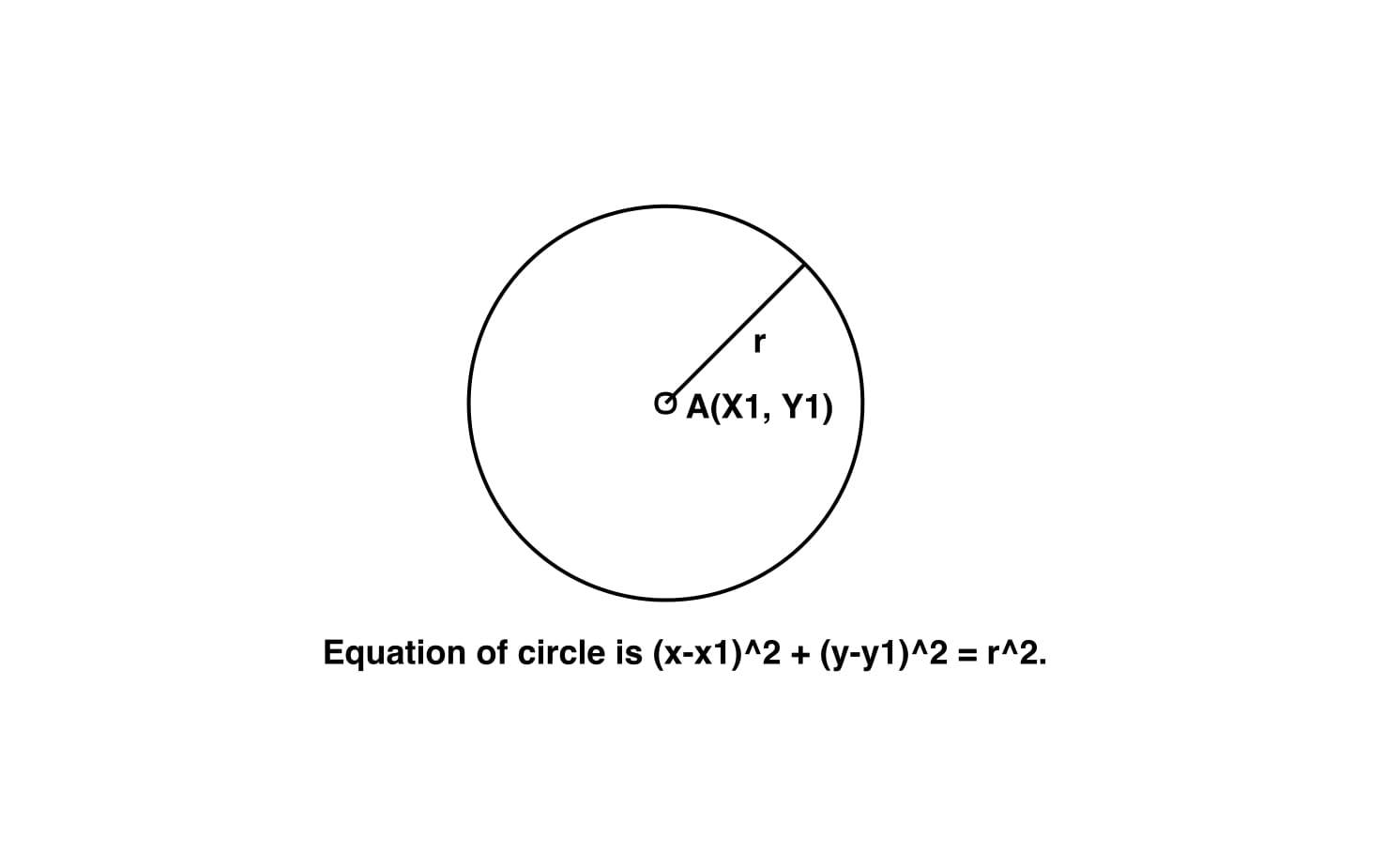
Dado el centro del círculo (x1, y1) y su radio r, encuentre la ecuación del círculo que tiene centro (x1, y1) y radio r.
Ejemplos: 
 

Entrada: x1 = 2, y1 = -3, r = 8 
Salida: x^2 + y^2 – 4*x + 6*y = 51.
Entrada: x1 = 0, y1 = 0, r = 2 
Salida: x ^2 + y^2 – 0*x + 0*y = 4.
 

Planteamiento: 
Dado el centro del círculo (x1, y1) y su radio r, tenemos que encontrar la ecuación del círculo que tiene centro (x1, y1) y radio r. 
la ecuación del círculo con centro (x1, y1) y radio r viene dada por:- 
 

al expandir la ecuación anterior 
 

al organizar arriba obtenemos 
 

A continuación se muestra la implementación del enfoque anterior: 
 

// CPP program to find the equation
// of circle.
#include <iostream>
using namespace std;
 
// Function to find the equation of circle
void circle_equation(double x1, double y1, double r)
{
    double a = -2 * x1;
 
    double b = -2 * y1;
 
    double c = (r * r) - (x1 * x1) - (y1 * y1);
 
    // Printing result
    cout << "x^2 + (" << a << " x) + ";
    cout << "y^2 + (" << b << " y) = ";
    cout << c << "." << endl;
}
 
// Driver code
int main()
{
    double x1 = 2, y1 = -3, r = 8;
    circle_equation(x1, y1, r);
    return 0;
}

// Java program to find the equation
// of circle.
import java.util.*;
 
class solution
{
 
 // Function to find the equation of circle
static void circle_equation(double x1, double y1, double r)
{
    double a = -2 * x1;
 
    double b = -2 * y1;
 
    double c = (r * r) - (x1 * x1) - (y1 * y1);
 
    // Printing result
    System.out.print("x^2 + (" +a+ " x) + ");
     System.out.print("y^2 + ("+b + " y) = ");
     System.out.println(c +"." );
}
 
// Driver code
public static void main(String arr[])
{
    double x1 = 2, y1 = -3, r = 8;
    circle_equation(x1, y1, r);
  
}
 
}

# Python3 program to find the
# equation of circle.
 
# Function to find the
# equation of circle
def circle_equation(x1, y1, r):
    a = -2 * x1;
 
    b = -2 * y1;
 
    c = (r * r) - (x1 * x1) - (y1 * y1);
 
    # Printing result
    print("x^2 + (", a, "x) + ", end = "");
    print("y^2 + (", b, "y) = ", end = "");
    print(c, ".");
 
# Driver code
x1 = 2;
y1 = -3;
r = 8;
circle_equation(x1, y1, r);
 
# This code is contributed
# by mits

// C# program to find the equation
// of circle.
using System;
 
class GFG
{
 
// Function to find the equation of circle
public static void circle_equation(double x1,
                                   double y1,
                                   double r)
{
    double a = -2 * x1;
 
    double b = -2 * y1;
 
    double c = (r * r) - (x1 * x1) - (y1 * y1);
 
    // Printing result
    Console.Write("x^2 + (" + a + " x) + ");
    Console.Write("y^2 + ("+ b + " y) = ");
    Console.WriteLine(c + "." );
}
 
// Driver code
public static void Main(string []arr)
{
    double x1 = 2, y1 = -3, r = 8;
    circle_equation(x1, y1, r);
}
}
 
// This code is contributed
// by SoumkMondal

<?php
// PHP program to find the equation
// of circle.
 
// Function to find the
// equation of circle
function circle_equation($x1, $y1, $r)
{
    $a = -2 * $x1;
 
    $b = -2 * $y1;
 
    $c = ($r * $r) - ($x1 * $x1) -
                     ($y1 * $y1);
 
    // Printing result
    echo "x^2 + (" . $a . " x) + ";
    echo "y^2 + (" . $b . " y) = ";
    echo $c . "." . "\n";
}
 
// Driver code
$x1 = 2; $y1 = -3; $r = 8;
circle_equation($x1, $y1, $r);
 
// This code is contributed
// by Akanksha Rai
?>

<script>
// java script  program to find the equation
// of circle.
 
// Function to find the
// equation of circle
function circle_equation(x1, y1, r)
{
    let a = -2 * x1;
 
    let b = -2 * y1;
 
    let c = (r * r) - (x1 * x1) -
                    (y1 * y1);
 
    // Printing result
    document.write( "x^2 + (" +a + " x) + ");
    document.write( "y^2 + (" +b+ " y) = ");
    document.write( c+ "<br>");
}
 
// Driver code
let x1 = 2;
let y1 = -3;
let r = 8;
circle_equation(x1, y1, r);
 
// This code is contributed by sravan kumar
</script>

x^2 + (-4 x) + y^2 + (6 y) = 51.

Complejidad temporal: O(1), ya que no hay bucle ni recursividad.
Espacio Auxiliar: O(1), ya que no se ha ocupado ningún espacio extra.