Ecuación lineal en dos variables

Una ecuación lineal se define como una ecuación con el grado máximo de uno solo, por ejemplo, ax = b se puede denominar una ecuación lineal, y cuando aparece una ecuación lineal en dos variables, significa que la ecuación completa tiene 2 variables presentes en él. Por lo tanto, la Ecuación Lineal en dos variables se puede escribir en la forma general de, ax + by + c = 0, donde a, b, c son las constantes yx, y son las variables.

Ecuación lineal en dos variables 

Una ecuación lineal en dos variables viene dada por, 

Hacha + Por + C = 0

Donde, A, B y C son números reales constantes, y A y B nunca son cero. 

Veamos cómo formular tal ecuación a través de un ejemplo de la vida real. 

Pregunta: Se jugó un partido internacional de un día entre Australia e India en Nagpur. Dos bateadores indios anotaron un total de 176 carreras. Exprese esta información en forma de ecuación. 

Responder:

Sabemos que dos bateadores anotaron 176 carreras, pero no sabemos cuánto anotó cada bateador. Sean «x» e «y» las carreras anotadas por cada bateador. 

Entonces, x + y = 176. 

Esta es la ecuación lineal requerida en dos variables. 

Las ecuaciones lineales en una variable también se pueden representar como una ecuación lineal en dos variables. Por ejemplo: x = 3, también se puede reescribir como 

x.1 + y.0 = 3

Soluciones de Ecuación Lineal en dos Variables 

Hemos visto ecuaciones como x = 5, y = 10. Solo tienen una solución. Pero cuando se trata de ecuaciones lineales en dos variables. Hay más de una solución, 

Por ejemplo: Supongamos una ecuación en dos variables, 

x + 2y = 4

Para encontrar las soluciones a esta ecuación, necesitamos saber los valores de x e y que satisfacen esta ecuación. Aquí x = 2 y y = 1 es una solución, vamos a verificarlo. Introduce los valores de x e y en la ecuación anterior. 

x + 2y = 4

⇒ (2) + 2(1) = 4

⇒ 2 + 2 = 4

Por lo tanto, x = 2 y y = 1 es una solución de esta ecuación. De manera similar, también podemos verificar que x = 2 y y = 1 también es una solución. Podemos hacer más soluciones como esta simplemente asumiendo un valor de x y luego introduciendo la ecuación. Por ejemplo: supongamos que x = 4. Ahora introdúzcalo en la ecuación, la ecuación se reduce a una ecuación de una sola variable. 

4 + 2y = 4 

⇒2y = 0 

⇒ y = 0

Entonces, si seguimos tomando diferentes valores de x, podemos encontrar infinitas soluciones a estas ecuaciones. 

Así, podemos decir que las Ecuaciones Lineales en dos variables tienen infinitas soluciones. 

Pregunta 1: Encuentra tres soluciones diferentes para la ecuación y + 5x = 10. 

Solución:

Para encontrar diferentes soluciones, simplemente tenemos que asumir un valor de x o y. Conéctelo en la ecuación y redúzcalo en una ecuación de una sola variable. De esta manera podemos encontrar el valor de otra variable. 

Digamos x = 2. Conéctalo en la ecuación, 

y + 5(2) = 10 

⇒ y + 10 = 10 

⇒ y = 0

Entonces, (2,0) es una solución. 

Ahora digamos x = 3 e introdúzcalo en la ecuación, 

y + 5(3) = 10 

⇒ y + 15 = 10 

⇒ y = 10 – 15 

⇒ y = -5 

La solución resulta ser (3, -5) 

Para la última solución requerida, asuma x = 0 y conéctelo, 

y + 5(0) = 10 

⇒ y = 10 

La solución resulta ser (2,10) 

Así, las tres soluciones son:- (2,0); (3,-5) y (2,10). 

Gráfica de Ecuación Lineal en Dos Variables

Hasta ahora hemos visto soluciones de ecuaciones lineales. Hay infinitas soluciones para una ecuación lineal en dos variables. Veamos su interpretación geométrica. Podemos mostrar todas las soluciones en un plano de coordenadas y ver cómo se ve. Veamos cómo hacer esto. 

Tomemos un ejemplo, x + 2y = 6. 

Sus soluciones se pueden organizar en la forma de la tabla que se muestra a continuación. 

X	0	2	4	6
y	3	2	1	0

Grafiquemos (0,3); (2,2); (4,1) y (6,0) en el gráfico. 

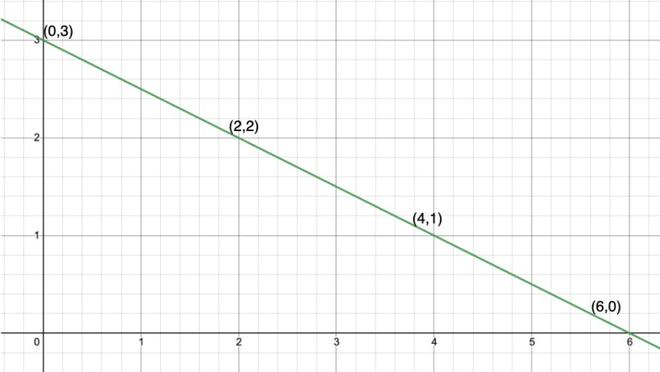
Observe que todos estos puntos cuando se unen forman una línea recta. Cada punto en esta línea satisface la ecuación y cada solución de esta ecuación está en la línea. Esto se llama un gráfico de la ecuación lineal. Para trazar la gráfica de una ecuación lineal, requerimos un mínimo de dos soluciones de la ecuación. 

Representación gráfica de ecuaciones lineales mediante el trazado de puntos:

1. Encuentra tres puntos cuyas coordenadas sean soluciones a la ecuación.
2. Marca los puntos en un gráfico.
3. Dibuja una línea a través de los tres puntos.

Tomemos un ejemplo,

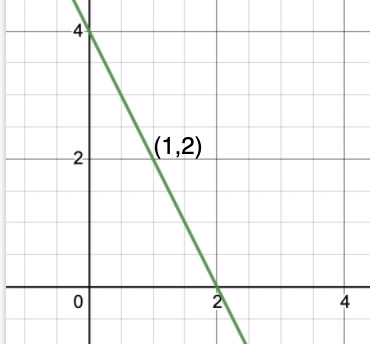
Pregunta: Trace la ecuación de la línea 2x + y = 4 usando el método mencionado anteriormente. 

Solución: 

Primero busquemos tres puntos que satisfagan esta ecuación. Esto se hace por el método discutido anteriormente.

Pongamos x = 0, luego y resulta ser y = 4. Entonces (0,4) es un punto. 

Poniendo y = 0, obtenemos, x = 2. Entonces (2,0) es otro punto. 

Poniendo x = 1, obtenemos y = 2. Entonces (1,2) es el tercer punto. 

X	y
0	4
2	0
1	2

Tracemos los puntos dados en la tabla y unámoslos para formar una línea. 

La figura representa nuestra línea requerida. 

Ecuación de rectas paralelas al eje x y al eje y

Consideremos la ecuación x = 3. 

Ahora, cuando esta ecuación se trata como una ecuación de una sola variable, solo tiene solución x = 3. Pero cuando la tratamos como una ecuación de dos variables 

x + 0.y = 3. Esta ecuación tiene infinitas soluciones. Tracemos gráficas de tales ecuaciones. 

Pregunta 1: Traza la ecuación de x = 4.  

Solución:

Encontremos la solución para esta ecuación. 

x + 0.y = 4

x = 4 satisface la ecuación, y podemos poner cualquier valor en lugar de y, no afectará la solución. Por lo tanto, las soluciones a esta ecuación se ven así, 

X	4	4	4
y	0	1	2

Tracemos estos puntos en el gráfico y obtengamos la línea. 

Pregunta 2: Trace la gráfica de y = 3. 

Solución:

Encontremos la solución para esta ecuación. 

0.x + y = 3

y = 3 satisface la ecuación, y podemos poner cualquier valor en lugar de y, no afectará la solución. Por lo tanto, las soluciones a esta ecuación se ven así, 

X	0	1	2
y	3	3	3

Tracemos estos puntos en el gráfico y obtengamos la línea. 

Pregunta 3: La tarifa de un taxi en Bangalore es la siguiente: para el primer kilómetro es de 10 rupias y luego la distancia posterior se mide en 5 rupias por kilómetro. Formule la ecuación lineal para este problema y dibuje su gráfica. 

Solución:

Sea la distancia total recorrida por “x” Km y la tarifa total sea “y”. 

y = 10 + (x – 1)5 

⇒ y= 10 + 5x -5 

⇒ y = 5x + 5 

Ahora busquemos las soluciones de esta ecuación y grafiquémosla. 

X	-1	0	2
y	0	5	15

La tabla representa tres soluciones de la ecuación. Tracemos estos puntos en el gráfico y unámoslos para formar una línea recta. 

Pregunta 4: Rahul y Ravi contribuyeron con un total de 100 rupias al Fondo de Ayuda Covid establecido por el gobierno. Formule la ecuación que satisfaga los datos y trace su gráfica.

Responder:

Que la contribución de Rahul sea Rs. x y el de Ravi ser Rs. y. 

Entonces la ecuación se puede formar como, 

x + y = 100 

Nuevamente, encontremos algunas soluciones a esta ecuación.

X	20	40	60
y	80	60	40

Trazar los puntos en el gráfico.