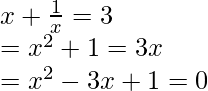Ecuaciones cuadráticas

Los polinomios son de diferentes tipos, de los cuales dos polinomios de grado tienen la forma ax ² + bx + c, a ≠ 0. Cuando igualamos este polinomio a cero, obtenemos una ecuación cuadrática. Este tipo de ecuaciones surgen en muchas situaciones de la vida real. Estudiemos este tipo de ecuaciones, cómo resolverlas y cómo formularlas en situaciones de la vida real. 

Por ejemplo, una junta escolar decide hacer un campo de fútbol para sus alumnos. Han decidido que la superficie del campo de fútbol será de 1000 m ² . El entrenador indica que la longitud del terreno debe ser 50 metros más que el doble del ancho del terreno. Necesitamos encontrar cuál debe ser el largo y el ancho del suelo. 

Digamos que el ancho del suelo es «x». Entonces la longitud del suelo será “2x + 50”. Sabemos que el área debe ser de 1000m ² . Asi que, 

x(2x + 50) = 1000 

⇒2×2 ⁺ 50x = 1000

⇒2×2 ⁺ 50x – 1000 = 0

Aquí obtenemos una ecuación cuadrática. Definamos formalmente la ecuación cuadrática. 

Ecuación cuadrática

Una ecuación cuadrática en la variable «x» es una ecuación de la forma, 

hacha ² + bx + c = 0

Donde, a, b, c son números reales y constantes y a ≠ 0.

Ejemplo: 4x ² – 5x = 0, 5x ² + 16x + 5 = 0

En general, cualquier polinomio de segundo grado P(x), cuando se expresa como P(x) = 0, representa una ecuación cuadrática. 

Pregunta 1: Rahul y Ravi juntos tienen 45 dulces. Ambos perdieron 5 dulces cada uno. El producto de la cantidad de dulces que ambos tienen ahora es 124. Se nos pide que averigüemos la cantidad de dulces que tenía cada uno al principio. Formule una ecuación cuadrática para este problema. 

Solución:

Digamos que Rahul tenía «x» dulces. Entonces Ravi debe tener “45 – x” dulces porque ambos tenían 45 dulces. 

Ahora después de perder los dulces, nos dan que el producto de la cantidad de dulces que tienen es 124. Es decir, 

x(45 – x) = 124

⇒ 45x – x2 ⁼ 124 

^{⇒ 0} = x2 – 45x + 124

Pregunta 2: Comprueba si la siguiente ecuación es una ecuación cuadrática o no. 

(x – 2)(x + 1) = (x – 1)(x + 3) 

Solución:

Sabemos que una ecuación cuadrática debe ser de grado 2. 

Simplifiquemos y comprobemos la ecuación dada. 

 (x – 2)(x + 1) = (x – 1)(x + 3)

⇒ x2 + x – 2x – 2 = x2 ⁺ 3x – x – ³

⇒ x2 – x – 2 = x2 ^{+ 2x} – 3

⇒ -x – 2 = 2x – 3 

⇒ -3x + 1 = 0  

Esta ecuación es de grado 1. Por lo tanto, no puede ser una ecuación cuadrática. 

Resolver una ecuación cuadrática

Supongamos una ecuación cuadrática P(x) = 0. Los puntos que satisfacen esta ecuación se llaman soluciones o ceros de esta ecuación cuadrática. Hay tres tipos de métodos para encontrar la solución de una ecuación cuadrática: 

1. Método de factorización
2. Completar el método de los cuadrados
3. Shree Dharacharya o fórmula cuadrática

Veamos estos tres métodos uno por uno a través de ejemplos. 

Método de factorización

Una ecuación cuadrática puede considerarse un factor de dos términos. Como ax ² + bx + c = 0 se puede escribir como (x – x ₁ )(x – x ₂ ) = 0 donde x ₁ y x ₂ son raíces de la ecuación cuadrática.

Pasos para resolver:

1. Encuentra dos números tales que el producto de los números sea ‘ac’ y la suma sea ‘b’.
2. Luego escribe el coeficiente x como la suma de estos dos números y divídelos de manera que obtengas dos términos para x.
3. Factoriza los dos primeros como un grupo y los dos últimos términos como otro grupo.
4. Tome factores comunes de estos y al igualar las dos expresiones con cero después de tomar factores comunes y reorganizar la ecuación obtenemos las raíces.

Pregunta 1: Encuentra las soluciones de la ecuación cuadrática dada usando el método de factorización. 

2x ² – 3x + 1 = 0

Solución:

2x ² – 3x + 1 = 0

⇒ 2x ² – 2x – x + 1 = 0

⇒ 2x(x – 1) – 1(x -1) = 0

⇒ (2x – 1)(x-1) = 0

Ahora esta ecuación será cero cuando cualquiera de estos dos términos de ambos términos sea cero

Entonces, poniendo 2x – 1 = 0, obtenemos x = 

Del mismo modo, x – 1 = 0, obtenemos x = 1 

Así, obtenemos dos raíces x = 1 y 

Pregunta 2: Encuentra las raíces de la siguiente ecuación cuadrática usando el mismo método. 

2x ² – x – 6 = 0

Solución: 

2x ² – x – 6 = 0

⇒ 2x ² – 4x. +3x – 6 = 0

⇒ 2x (x – 2) +3(x – 2) = 0 

⇒ (2x + 3) (x – 2) = 0 

Ahora, 

2x + 3 = 0 

x = 

x-2 = 0 

x = 2

Entonces, esta ecuación tiene raíces x = 2 y 

Completar el método de los cuadrados

Cualquier ecuación ax ² + bx + c = 0 se puede convertir en la forma (x + m) ² – n ² = 0. Después de esto, tome las raíces cuadradas y obtenga las raíces de la ecuación. Completar el cuadrado es solo una forma de reajustar la ecuación cuadrática dada de tal manera que vengan en forma de cuadrados completos. Veamos esto a través de un ejemplo.

Pregunta 1: Encuentre la raíz de la ecuación dada completando el método del cuadrado. 

x2 ⁺ 4x – 5 = 0

Solución:

Nos dan, x ² + 4x – 5 = 0 

Para resolverlo completando el método del cuadrado, necesitamos traerlo en la forma mencionada anteriormente. 

x2 ⁺ 4x – 5 = 0

⇒ x2 ⁺ 4x + 4 – 9 = 0

⇒ (x + 2) ² – 3 ² = 0

⇒ (x + 2) ² = 3 ²

Tomando raíces cuadradas en ambos lados, 

x + 2 = 3 y x + 2 = -3 

Esto nos da x = 1, -5

Pregunta 2: Encuentre la raíz de la ecuación dada completando el método del cuadrado. 

x2 ⁺ 6x + 9 = 0

Solución:

Dado,x ² + 6x + 9 = 0

x2 ⁺ 6x + 9 = 0

⇒ x2 + ² (3x) + 3 ² = 0

⇒ (x + 3) ² = 0 

Tomando la raíz cuadrada, 

x + 3 = 0 

x = – 3

Por lo tanto, esta ecuación tiene una sola raíz con multiplicidad de 2. 

x = -3,-3

Shree Dharacharya o fórmula cuadrática 

Esta fórmula dice, 

Para una ecuación cuadrática en forma general, 

hacha ² + bx + c = 0

Si b ² – 4ac > 0, 

Entonces las raíces están dadas por 

Pregunta 1: Encuentra las raíces de la ecuación 3x ² – 5x + 2 = 0.

Solución: 

Para descubrir las raíces usando la fórmula Shree Dharacharya, 

Necesitamos comprobar si b ² – 4ac > 0,

En esta ecuación particular, a = 3, b = -5 y c = 2. 

Entonces, b ² – 4ac 

⇒ (-5) ² – 4(3)(2) 

⇒ 25 – 24 

⇒ 1 > 0 

Por lo tanto, las raíces son posibles, 

Ahora calculemos las raíces reemplazando los valores en la fórmula mencionada anteriormente. 

Pregunta 2: Encuentra las raíces de la ecuación

 

Solución:

Primero debemos simplificar esta ecuación y llevarla a la forma cuadrática para que podamos aplicar la fórmula Dharacharya. 

 

Ahora comprobemos si b ² – 4ac > 0 primero. 

Aquí a = 1, b = -3 y c = 1

b2-4ac ^_ _ 

⇒ 9. -4(1)(1) 

⇒ 5 > 0 

Así que podemos aplicar la fórmula ahora,