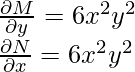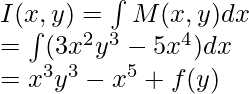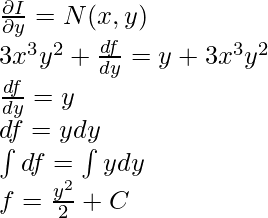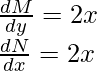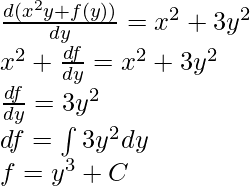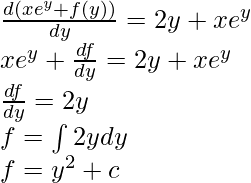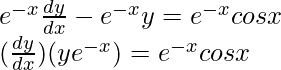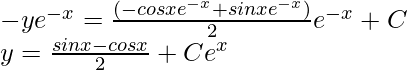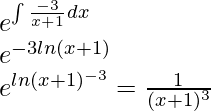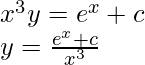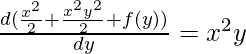Ecuaciones exactas y factores de integración

Las ecuaciones diferenciales se utilizan para describir muchos fenómenos físicos. Nos ayudan a observar algo que sucede en la vida real y ponerlo en forma matemática. En este nivel, nos interesan principalmente las ecuaciones diferenciales lineales y de primer orden. Una ecuación diferencial en “y” es lineal si todas las derivadas de y aparecen solo a la primera potencia. Entonces tiene la forma si todas las derivadas de y aparecen solo a la primera potencia. Entonces tiene la forma,

$A_{n}y^{n}+A_{n-2}y^{n-1}+...+A_{1}y'+A_{0}y = f$

Se permite que los coeficientes dependan únicamente de las variables independientes. Tenga en cuenta que el orden puede ser arbitrariamente grande. Vamos a ver las ecuaciones diferenciales exactas. Estas ecuaciones son ecuaciones diferenciales de primer orden.

Ecuaciones diferenciales exactas

Es una ecuación diferencial de primer orden que parece,

M(x, y)dx + N(x, y)dy = 0

Tiene una función especial I(x, y) cuyas derivadas parciales se pueden poner en lugar de M y N como,

$\frac{\partial{I}}{\partial{x}}dx + \frac{\partial{I}}{\partial{y}}dy = 0$

Resolver estas ecuaciones significa encontrar que la función I(x, y) = C.

Comprobando si una ecuación es exacta o no:

Supongamos que existe una función solución I(x, y). Después,

$\frac{\partial{M}}{\partial{y}} = \frac{\partial^{2}{I}}{\partial{x}\partial{y}}{}$

$\frac{\partial{N}}{\partial{x}} = \frac{\partial^{2}{I}}{\partial{x}\partial{y}}{}$

Deberían terminar igual. Entonces, para verificar si la ecuación es exacta o no, simplemente calcula estas derivadas parciales. Entonces, ahora que hemos comprobado que la ecuación es exacta, pasaremos a encontrar la solución a esta ecuación.

Cálculo de la solución de ecuaciones diferenciales exactas:

La solución general se puede calcular de cualquiera de las siguientes formas:

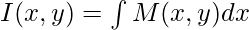$I(x,y) = \int M(x,y)dx$ (con x como variable independiente)
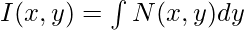$I(x,y) = \int N(x,y)dy$ (con y como variable independiente)

Entonces, entonces la solución general se convierte en,

yo(x, y) = C

Problemas de muestra

Pregunta 1: Resuelve: (3x ² y ³ – 5x ⁴ )dx + (y + 3x ³ y ² )dy = 0

Solución:

Aquí, M(x, y) =3x ² y ³ – 5x ⁴ y N(x, y) = y + 3x ³ y ²

Primero verifica si esta ecuación es exacta o no,

$\frac{\partial{M}}{\partial{y}} = 6x^{2}y^{2} \\ \frac{\partial{N}}{\partial{x}} = 6x^{2}y^{2}$

Como ambos son iguales, la ecuación es exacta.

Ahora encontremos la solución de esta ecuación,

yo $I(x,y) = \int M(x,y)dx \\ \hspace{1.1cm}= \int (3x^{2}y^{3} - 5x^{4})dx \\ \hspace{1.1cm}= x^{3}y^{3} - x^{5} + f(y)$

Observe que estamos escribiendo f(y) en lugar de la constante de integración “C”, porque teníamos y como un parámetro fijo mientras lo integrábamos, pero sabemos que es una variable, por lo que necesitamos calcular f(y).

Sabemos, $\frac{\partial{I}}{\partial{y}} = N(x,y)\\ 3x^{3}y^{2} + \frac{df}{dy} = y + 3x^{3}y^{2} \\ \frac{df}{dy} = y \\ df = ydy \\ \int df = \int ydy \\ f = \frac{y^{2}}{2} + C$

Sustituyamos f(y) en la solución general,

$I(x,y) =x^{3}y^{2} - x^{5} + \frac{y^{2}}{2} + C$

Esta es la solución general para esta ecuación diferencial exacta.

Pregunta 2: Resuelva la ecuación diferencial para lo siguiente:

(x ² + 3y ² )dy + 2xydx = 0

Solución:

M(x, y) = 2xy, N(x, y)=x ² +3y ²

$\frac{dM}{dy}= 2x\\\frac{dN}{dx}=2x$

Por lo tanto, la ecuación es exacta.

Solución de esta ecuación: I(x, y)= $\int M(x,y)dx= \int(2xy)dx\\=x^2y+f(y)\\ \frac{dI}{dy}=N(x,y)$

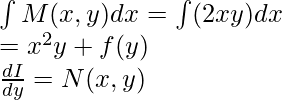
Sustituyendo I(x, y) se obtiene:

$\frac{d(x^2y+f(y))}{dy}=x^2+3y^2\\ x^2+ \frac{df}{dy}=x^2+3y^2\\\frac{df}{dy}=3y^2\\df=\int3y^2dy\\f=y^3+C$

Pon el valor de f(y) en I(x, y):

yo(x, y)= x ² y+y ³ +C

Esta es la solución general para la ecuación diferencial exacta.

Pregunta 3: Resuelve e ^y dx +(2y+xe ^y )dy = 0

Solución:

M(x, y) = e ^y , N(x, y) = (2y+xe ^y )

Resolviendo $\frac{dM}{dy},\frac{dN}{dx}$

$\frac{dM}{dy}=e^y,\frac{dN}{dx}=e^y$

Por lo tanto, la ecuación dada es una ecuación exacta.

Solución de la ecuación: I(x, y) = $\int M(x,y)dx= e^ydx=xe^y+f(y)$

Se sabe que dI/dy = N(x, y)

Sustituyendo I(x, y):

$\frac{d(xe^y+f(y))}{dy}=2y+xe^y\\xe^y+\frac{df}{dy}=2y+xe^y\\\frac{df}{dy}=2y\\f=\int2ydy\\f=y^2+c$

Por lo tanto, la solución para la ecuación exacta obtenida es,

yo(x, y) = xe ^y + y ² + C

factor de integración

Este es también otro método para resolver ecuaciones diferenciales lineales.

$\frac{dy}{dx} + Py = Q$

La ecuación anterior representa una ecuación diferencial lineal de primer orden. P y Q son constantes o funciones de x. Los siguientes pasos brindan un esquema de cómo resolver la ecuación lineal de primer orden de esta forma usando el factor de integración.

Paso 1: Escriba la ecuación diferencial dada en la forma $\frac{dy}{dx} + Py = Q$ , donde P y Q son constantes o funciones de x solamente.

Paso 2: encuentre el factor de integración $I.F = e^{\int Pdx}$

Paso 3: Escriba la solución de la ecuación diferencial como $y(I.F) = Q(I.F)dx + C$

Nota: En caso de que la ecuación diferencial de primer orden tenga la forma $\frac{dx}{dy} + P_{1}x = Q_{1}$ , donde P ₁ y Q ₁ son constantes o funciones de y solamente. Entonces $I.F = e^{\int P_{1}dx}$ y la solución de la ecuación diferencial está dada por $x.(I.F) = \int (Q_{1} \times I.F)dy + C$

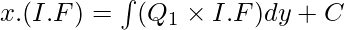
Problemas de muestra

Pregunta 1: Encuentra la solución general de la siguiente ecuación,

$\frac{dy}{dx} - y = cosx$

Solución:

La ecuación coincide con la forma dada arriba, así que aquí P = -1 y Q = cosx.

Por lo tanto , $I.F = e^{\int -dx} = e^{-x}$

Multiplicando ambos lados de la ecuación por SI

$e^{-x}\frac{dy}{dx} - e^{-x}y = e^{-x}cosx \\ (\frac{dy}{dx})(ye^{-x}) = e^{-x}cosx \\$

Integrando ambos lados de la ecuación por SI, obtenemos

$ye^{-x} = \int e^{-x}cosxdx + C \\ \text{Let, } \\ I = \int e^{-x}cosxdx\\ = cosx(-e^{-x}) - \int (-sinx)(e^{-x})dx \\ = -cosx(e^{-x}) - \int sinxe^{-x}dx \\ = -cosxe^{-x} + sinxe^{-x} - \int cosxe^{-x} \\ I = -cosxe^{-x} + sinxe^{-x} - I \\ 2I = (-cosxe^{-x} + sinxe^{-x})\\ I = \frac{(-cosxe^{-x} + sinxe^{-x})}{2}$

Poniendo este valor en la ecuación original,

$-ye^{-x} = \frac{(-cosxe^{-x} + sinxe^{-x})}{2}e^{-x} + C \\ y = \frac{sinx - cosx}{2} + Ce^{x}$

Esta es la solución general de la ecuación diferencial dada.

Pregunta 2: Encuentra la solución general de la ecuación diferencial,

$\frac{dy}{dx}-\frac{3y}{x+1}=(x+1)^4$

Solución:

P= -3/(x+1), Q=(x+1) ⁴

Primero, encuentre el SI,

SI= $e^{\int\frac{-3}{x+1}dx}\\e^{-3ln(x+1)}\\e^{ln(x+1)^{-3}}=\frac{1}{(x+1)^3}$

Multiplicar por Factor de integración en ambos lados:

$\frac{1}{(x+1)^3}\frac{dy}{dx}-\frac{3y}{(x+1)^4}=(x+1)$

Integrar ambos lados:

$\frac{y}{(x+1)^3}=0.5x^2+x+c$

Por lo tanto, la ecuación general es:

y = (x+1)3(0.5x ² +x+c)

Pregunta 3: ¿La solución general de la ecuación diferencial será?

$\frac{dy}{dx}+\frac{3y}{x}=\frac{e^x}{x^3}$

Solución:

Primero, encuentre el I.F’

P = 3/x, Q = e ^x /x ³

SI = $e^{\int\frac{3}{x}dx}=e^{3lnx}=e^{lnx^3}=x^3$

Por lo tanto, SI = x ³

Multiplique el factor de integración en ambos lados,

$x^3\frac{dy}{dx}+3x^2y=e^x$

Integrar ambos lados,

$x^3y=e^x+c\\y=\frac{e^x+c}{x^3}$

Factores especiales de integración

Hasta ahora hemos aprendido todo sobre las ecuaciones diferenciales exactas y cómo resolverlas, pero hay veces que nos encontramos con ciertas ecuaciones que son «casi exactas» pero no ecuaciones diferenciales exactas, ya que no son exactas pero se forman a partir de ecuaciones diferenciales exactas haciendo algunos cambios en ellos. Si podemos retroceder y hacer que la ecuación sea exacta nuevamente, el problema se resolverá fácilmente.

Para rastrear el factor de integración exacto, multiplique la ecuación con un ‘factor de integración especial’ conocido como $\mu(x)$ OR $\mu(y)$ (según el enunciado del problema).

Factor de integración usando solo x

Supongamos que se da la ecuación casi exacta, M(x, y) dx + N(x, y) dy =0 [Casi exacta]

Multipliquemos esto con el factor integrante especial $\mu(x)$

$\mu(x)$ × M(x, y) dx + $\mu(x)$ × N(x, y) dy =0

Ahora, para que la ecuación anterior sea exacta, tiene que haber algún valor de $\mu(x),$ la fórmula para el factor de integración especial,

$\mu(x)=e^{\int{\frac{dM/dy-dN/dx}{N}dx}}$

Pregunta: Resuelve la ecuación diferencial, (1+y ² )dx+ xydy = 0

Solución:

Para empezar, primero tenemos que comprobar la exactitud de la ecuación diferencial

dM/dy = 2y, dN/dx = y

Ahora, como la ecuación no es exacta, necesitamos encontrar el factor de integración que se necesita ajustar en la ecuación para que sea exacta.

(dM/dy-dN/dx) = 2y-y = y

1/N{dM/dy-dN/dx}=y/(xy)= 1\x

Aquí, nos dimos cuenta de que la ecuación depende solo de x.

Por lo tanto, el factor integrante es $\mu(x)$

$\frac{1}{\mu}\frac{d\mu}{dx}=\frac{1}{x}$

Separe las variables e integre ambos lados,

$ln\mu= lnx$

$\mu= ^+_-x$

Obtuvimos el valor del factor integrante, multiplicamos esto con nuestra ecuación original

(x+xy ² )dx + x ² ydy=0

Comprobando la exactitud de nuevo,

dM/dy= 2xy, dN/dx= 2xy

Integrar M y N como de costumbre,

M(x, y)= $\int(x+xy^2)dx=\frac{x^2}{2}+\frac{x^2y^2}{2}+f(y)$

Sustituir para determinar f(y)

$\frac{d(\frac{x^2}{2}+\frac{x^2y^2}{2}+f(y))}{dy}=x^2y$

Sigue f(y)=C donde, C es una constante.

Por lo tanto, la solución general se convierte en,

$\frac{x^2}{2}+\frac{x^2y^2}{2}+C=0$

Factor de integración usando solo y

De manera similar, la ecuación exacta se puede obtener multiplicando la ecuación casi exacta con el factor de integración especial $\mu(y)$ , la fórmula se da como,

$\mu(y)=e^{\int{\frac{dN/dx-dM/dy}{M}dy}}$

Pregunta: Resolver la ecuación diferencial, (2y ² +2y+4x ² )dx + (2xy +x) dy = 0

Solución:

Para empezar, tenemos que comprobar si la siguiente ecuación es exacta o no,

dM/día = (4y +2), dN/dx = (2y +1)

dM/dy ≠ dN/dx {la ecuación no es exacta}

Para encontrar el factor de integración, resuelve el valor de $\frac{dM/dy-dN/dx}{N}= \frac{(4y+2)-(2y+1)}{2xy+x}$

$\frac{(2y+1)}{x(2y+1)}$ =1/x

Dado que el valor obtenido es puramente una función de x, podemos concluir que el factor de integración especial es $\mu(x)$

$\mu(x)=e^{1/xdx}$ = e ^lnx = x

Multiplique el factor integrante especial con la ecuación original,

x[(2y ² +2y+4x ² )dx + (2xy +x) dy]=0

(2xy ² +2xy+4x ³ )dx + (2x ² y +x ² ) dy=0

Encontrando la exactitud de la ecuación diferencial obtenida,

dM/dy=(4xy+2x), dN/dx=(4xy+2x)

Ahora podemos integrar M y N como de costumbre,

$\int{M(x, y)dx}=\int{(2xy^2+2xy+4x^3)dx}=x^2y^2+x^2y+x^4+C(y)$

$\int{N(x, y)dy}=\int{(2x^2y+x^2)dy}= x^2y^2+x^2y+C(x)$

Por lo tanto, Solución: x ² y ² +x ² y+x ⁴ =C