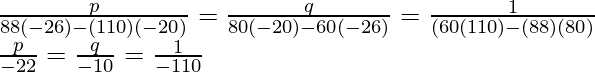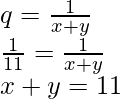Una ecuación lineal es un polinomio de un grado. Puede tener una o más de una variable en él. Por ejemplo, 2x + 5, 5x + 10y, etc., son algunos ejemplos de ecuaciones lineales. A veces, algunas ecuaciones no son de naturaleza lineal por defecto, pero se pueden llevar a la forma lineal.
Por ejemplo:
![]()
La ecuación dada arriba no es una ecuación lineal, pero se puede convertir en una forma lineal con algunos reordenamientos y métodos algebraicos. Veámoslos en detalle.
Ecuaciones reducibles a forma lineal
Veamos este procedimiento con un ejemplo.
Supongamos que tomamos la ecuación dada arriba ![]() . Esta ecuación no es de naturaleza lineal, sin embargo, si decidimos sustituirla
. Esta ecuación no es de naturaleza lineal, sin embargo, si decidimos sustituirla
![]()
Entonces esta ecuación se convierte en,
7p + 3q = 2
Ahora las soluciones a esta ecuación se pueden encontrar con «p» y «q» y luego podemos obtener las soluciones reales con la relación anterior,
![]()
Pregunta 1: Reduzca la siguiente ecuación a la forma lineal.
![]()
Solución:
Como se explicó anteriormente, digamos.
y
Sustituyendo estos valores en la ecuación, obtenemos
2p + q = 1
Ahora veamos cómo resolver un par de tales ecuaciones con un ejemplo,
Pregunta 2: Resuelve el sistema de ecuaciones dado
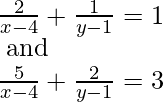
Solución:
Digamos,
p =
y q =
Entonces ambas ecuaciones se convierten en,
2p + q = 1 ……(1)
5p + 2q = 3 ……..(2)
Ahora tenemos que resolver estas ecuaciones,
De la ecuación (1),
q = 1 – 2p
Reemplazando este valor en la ecuación (2)
5p + 2(1 – 2p) = 3
⇒5p + 2 – 4p = 3
⇒ p + 2 = 3
⇒ p = 1
Entonces q = -1.
Ahora volvamos a las soluciones reales usando las expresiones que asumimos al principio.
p =
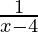
⇒ 1 =
⇒ x – 4 = 1
⇒ x = 5
Similarmente,
q =
⇒ -1 =
⇒ -y + 1 = 1
⇒ y = 0
Por tanto, la solución de este sistema de ecuaciones es x = 5 e y = 0.
Problemas de palabras
Pregunta 1: Un barco recorre 60 Km río arriba y 88 Km río abajo en 20 horas. En otro viaje, recorrió 80 Km río arriba y 110 Km río abajo en 26 horas. Averigüe la velocidad de la corriente y la velocidad del bote en aguas tranquilas.
Solución:
Supongamos que la velocidad del bote en aguas tranquilas es “x Km/h” y la velocidad de la corriente es “y Km/h”.
Entonces, la velocidad del bote río abajo = x + y
Y la velocidad del barco aguas arriba = x – y
Sabemos que, tiempo =
Entonces, para el primer viaje la ecuación será,
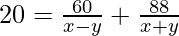
De manera similar, la ecuación para el segundo viaje será,
Estas ecuaciones ahora necesitan ser reducidas en una forma lineal,
Digamos p =
y
Sustituyendo esto en las ecuaciones anteriores, obtenemos
20 = 60p + 88q
26 = 80p + 110q
Resolviendo esto con el método de multiplicación cruzada,
Esto nos da,
p =
y q =
Ahora pon estos valores de «p» y «q» en la ecuación,
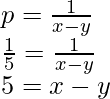
Para obtener los valores de «x» e «y» resolveremos estas ecuaciones,
x – y = 5 ….. (1)
x + y = 11 ….. (2)
Poniendo el valor de x = y + 5
y + 5 + y = 11
⇒2y = 6
⇒ y = 3
Entonces, x = 8
Entonces, la solución es x = 8 y y = 3.
Pregunta 2: La distancia entre dos ciudades es de 300Km. Una persona tiene que viajar de uno a otro usando Bus y Train ambos. Se tardan 4 horas en viajar si recorremos 60Km en tren y el resto lo recorremos en autobús. Si se recorren 100 km en tren y el resto en autobús, se tardan 10 minutos más. Encuentra la velocidad del tren y del autobús que ha estado circulando entre dos ciudades.
Solución:
Sea la velocidad del autobús «x» y la del tren «y».
Así que el tiempo total empleado,
Digamos
Ahora las dos ecuaciones se convierten en,
4 = 60p + 240q
= 100p + 200q
Resolviendo estas ecuaciones,
La solución resulta ser
Calculando los valores de x e y a partir de esto,
x = 60 y y = 80
Por tanto, la velocidad del autobús es de 60 km/h y la del tren es de 80 km/h.
Pregunta 3: La edad de Ramesh es el doble de la edad de su hijo. Hace cuatro años, la edad de su hijo era 20 años menor que la de su padre. Encuentra su edad actual.
Solución:
Sea la edad de Ramesh x y la edad de su hijo sea y
Las ecuaciones obtenidas son,
y= 2x ⇢ 1
y-4 = (x-4) +20 ⇢ 2
2x-4 = x-4 + 20
x = 20 años
Pregunta 4: Resuelva la siguiente ecuación y obtenga el valor de p y q,
1/(2p) – 1/q= 2
1/p + 1/(2q)= 10
Solución:
Como se ve claramente, las dos ecuaciones anteriores no tienen la forma de una ecuación lineal, ya que se dan los recíprocos de p y q.
simplificando,
(1/2)(1/p) – 1/q = 2
1/p + (1/2)(1/q) = 10
Sea 1/p= x y 1/q = y
Ahora, las ecuaciones se verán como,
1/2(x) – y = 2
x + 1/2(y) = 10
Simplificando aún más para encontrar los valores de x e y,
x-2y = 4 (1)
2x+ y= 20 (2)
Multiplicar la ecuación 2 por 2 para igualar ambas ecuaciones
x-2y= 4
4x+ 2y= 40
5x = 44
x = 44/5
y = 12/5
Por lo tanto, p= 1/x= 5/44
q= 1/y= 5/12
Pregunta 5: Hay 2 amigos, Aditya y Aman, ambos decidieron comprar algunos dulces y chocolates, ambos gastaron Rs. 200 en la compra de artículos, pero Aman gastó 4 más de la mitad de lo que gastó Aditya. Calcula la cantidad exacta gastada por ambos amigos.
Solución:
Deje que la cantidad gastada por Aditya y Aman sea a y b respectivamente,
Ahora, ambos gastaron colectivamente 200 rupias
a+ b= 200 (1)
Aman gastó 4 rupias más de la mitad de la cantidad de aditya
a/2 +4 = b (2)
Resolución de la ecuación (2)
a+ 8= 2b
a= 2b-8
Poniendo el valor de a en la ecuación (1)
2b- 8 +b = 200
3b = 208
b = 208/3 = Rs. 69,7 ∼ Rs. 70
b = $70
Poniendo el valor de b en la ecuación (1)
a = $130
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA