Ejemplos de preguntas sobre algoritmos | Conjunto 3 | Análisis de orden de tiempo

Pregunta 1: ¿Cuál es el límite asintótico de T(n)?

$T(n) = \sum_{i=2}^{n} log_{i}n = log_{2}n + log_{3}n + \ldots + log_{n}n$

θ( n*log(n) )
θ( norte ² )
θ( norte )
θ( n*log ² (n) )
θ( n ² *log ² (n) )

Respuesta: 3
Explicación: Para encontrar los límites superior e inferior apropiados, un enfoque que primero viene a la mente es expandir la notación sigma a términos únicos entre los que se pueden detectar algunos patrones. De esta forma, ayuda a definir algunos límites superiores e inferiores aceptables y su combinación podría conducir a una posible solución.

Con respecto a la especificación de estos límites, hay algunos consejos como los siguientes:

Esto es obvio que para cualquier k mayor que √, cada log _k n debe ser menor que log _√n n = 2, mientras que más que log _n n = 1. En lenguaje matemático:
1. Una pista sobre el límite SUPERIOR, para k > √:
  $\forall k \geq \sqrt{n}, log_{k}n \leq log_{\sqrt{n}}n = 2$
  
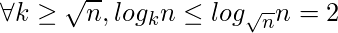
  $\Rightarrow \sum_{i=[\sqrt{n}]}^{ n } log_{i}n \leq \sum_{i=[\sqrt{n}]}^{ n } 2$
2. Una pista sobre el límite INFERIOR, para k > √:
  $\forall k \geq \sqrt{n}, log_{k}n \geq log_{n}n = 1$
  
  $\Rightarrow \sum_{i=[\sqrt{n}] + 1}^{ n } log_{i}n \geq \sum_{i=[\sqrt{n}] + 1}^{ n } 1$
Además, a medida que aumenta la base de un logaritmo, su valor disminuye; por lo que ninguno de los términos resultantes de la expansión del primer sigma puede ser mayor que el primer ter, log ₂ n, ni menor que el último, que es log _√norte; en otras oraciones,
1. Otra pista sobre el límite SUPERIOR, pero esta vez para k < √:
  $\forall k \leq \sqrt{n}, log_{k}n \leq log_{2}n$
  
  $\Rightarrow \sum_{i=2}^{ [\sqrt{n}] } log_{i}n \leq \sum_{i=2}^{ [\sqrt{n}] } log_{2}n$
2. Otra pista sobre el límite INFERIOR, pero esta vez para k < √:
  $\forall k \leq \sqrt{n}, log_{k}n \geq log_{\sqrt{n}}n = 2$
  
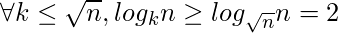
  $\Rightarrow \sum_{i=2}^{ [\sqrt{n}] } log_{i}n \geq \sum_{i=2}^{ [\sqrt{n}] } 2$

Siguiendo estos consejos da:

Límite inferior:
$\sum_{i=2}^{n} log_{i}n = \sum_{i=2}^{ [\sqrt{n}] } log_{i}n + \sum_{i=[\sqrt{n}]+1}^{n} log_{i}n$

$\leq \sum_{i=2}^{ [\sqrt{n}] } log_{2}n + \sum_{i=[\sqrt{n}]+1}^{n} 2$

$= ([\sqrt{n}] - 1) * log_{2}n + (n - [\sqrt{n}]) * 2$

$\approx 2 * n + \sqrt{n} * (log_{2}n - 2) - log_{2}n$

$\Rightarrow T(n) \in O( 2 * n + \sqrt{n} * (log_{2}n - 2) - log_{2}n ) = O( n )$
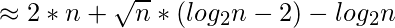
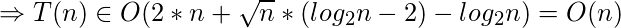
Limite superior:
$\sum_{i=2}^{n} log_{i}n = \sum_{i=2}^{ [\sqrt{n}] } log_{i}n + \sum_{i=[\sqrt{n}]+1}^{n} log_{i}n$

$\geq \sum_{i=2}^{ [\sqrt{n}] } log_{[\sqrt{n}]}n + \sum_{i=[\sqrt{n}]+1}^{n} 1$

$= ([\sqrt{n}] - 1) * 2 + (n - [\sqrt{n}]) * 1$

$\approx n + \sqrt{n} - 2$

$\Rightarrow T(n) \in \Omega(n + \sqrt{n} - 2) = \Omega( n )$

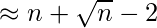
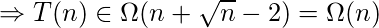
Lo deducido hasta ahora indica que el crecimiento de T(n) no puede exceder a O(n), ni puede ser menor que Ω(n); Por lo tanto, el orden de complejidad asintótica de T(n) es:

$T(n) \in \Theta(n)$

Pregunta 2: ¿Cuál es el orden de tiempo de ejecución de un programa dado?


  for(i= 2; i<n; i=i+1)
   for(j = 1; j < n; j= j * i)
    // A line of code of Θ(1)

θ( norte )
θ( n*log(n) )
θ( norte ² )
θ( n*log ² log(n) )
θ( n ² *log ² (n) )

Respuesta 1

Explicación: El tiempo de funcionamiento de cada línea se indica a continuación por separado:

La primera línea de código, t ₁ (n), es:
// se ejecuta (n – 2) veces; entonces la complejidad temporal de esta línea es de θ(n)
La segunda línea de código, t ₂ (n) es:
// log ₂ⁿ + log ₃ⁿ + … + log _n-1ⁿ = Σlog _iⁿ ∈ Θ( n ) según la PREGUNTA ANTERIOR de este artículo (Consulte la Pregunta 1)
La tercera línea de código, t ₃ (n) es:
::Dentro de los bucles, por lo que su tiempo de orden es el mismo que el de la línea anterior, que es de Θ( n )

La complejidad temporal total T(n) del programa es la suma de cada línea t _i (n), i = 1..3, como sigue:

$T(n) \in \Theta( n ) + \Theta( n ) + \Theta( n ) = \Theta( n )$

Pregunta 3: Se da la siguiente ecuación de recurrencia T(n). ¿Cuántas funciones propuestas g _i (n), i=1 .. 5, son aceptables para tener T(n) ∈ θ(f(n)) cuando f(n) = g _i (n)?

$T(n) = 8 * T(\frac{n}{2}) + f(n)$
$g_{1}(n) = n^{4}, g_{2}(n) = n^{3.01}, g_{3}(n) = n^{3},$
$g_{4}(n) = n^{3} * log(n), g_{5}(n) = n^{3} * log^{-1}(n)$

Respuesta: 2
Explicación: El teorema de Master y su extensión pueden ser de gran ayuda para abordar fácilmente este problema. La forma general del teorema maestro se puede expresar como:

$T(n) = a* T( \frac{n}{b}) + f(n), \forall a\geq 1, b > 1$

Para usar el teorema maestro , es necesario ver que el problema dado con «a», «b» y «f(n)» específicos satisface la condición de qué caso de este teorema. Los tres casos del teorema del maestro y sus condiciones son:

caso 1: este caso ocurre que el árbol de recurrencia tiene muchas hojas (el trabajo para dividir/recombinar un problema se ve eclipsado por los subproblemas).
$\forall \epsilon>0, f(n) \leq n^{log_{b}{a- \epsilon} } \Rightarrow T(n) \in \theta (n^{lob_{b}{a}})$
caso 2: Este caso ocurre cuando el trabajo para dividir/recombinar un problema es comparable a los subproblemas.
$f(n) \in \theta( n^{log_{b}{a}} * (log(n))^{k}) \Rightarrow T(n) \in \theta( n^{log_{b}{a}} *(log(n))^{k+1} )$
$\forall k \geq 0$
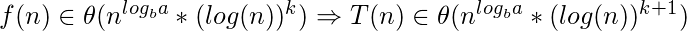
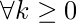
caso 3: este caso tiene lugar cuando el árbol de recurrencia tiene muchas raíces (el trabajo de dividir/recombinar un problema domina los subproblemas).
$\forall \epsilon>0, f(n) \geq n^{log_{b}{a + \epsilon} } \Rightarrow T(n) \in \theta (f(n))$

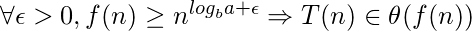
El segundo caso generalizado del teorema maestro, llamado teorema maestro avanzado , maneja todos los valores de k. Dice:

$\forall k > -1,$
$f(n) \in \theta( n^{log_{b}{a}} * (log(n))^{k}) \Rightarrow T(n) \in \theta( n^{log_{b}{a}} *(log(n))^{k+1} )$
$k = -1,$
$f(n) \in \theta( n^{log_{b}{a}} * (log(n))^{-1}) \Rightarrow T(n) \in \theta( n^{log_{b}{a}} *log(log(n)) )$
$\forall k < -1,$
$f(n) \in \theta( n^{log_{b}{a}} * (log(n))^{k}) \Rightarrow T(n) \in \theta( n^{log_{b}{a}} )$

La respuesta a esta pregunta es el tercer caso del teorema maestro donde T(n) es de Θ( f(n) ); entonces, para tener T(n) = θ(f(n)), debe haber una diferencia polinomial “epsilon” entre n ^{log _b a} y f(n); por tanto, las funciones g ₁ (n) y g ₂ (n) cumplen las condiciones del tercer caso del teorema de Master. Los valores de “épsilon” encontrados para ellos son 1 y 0,01 respectivamente.

Pregunta 4: ¿Qué opción delinea un verdadero análisis asintótico para este programa de múltiples variables de entrada, al tiempo que tiene una idea (conocimiento previo) sobre el crecimiento relativo de las entradas, como m ∈ Θ(n)?


  for(i= 1; i<= n; i=i+1) : n
   for(j = 1; j <= m; j= j * 2)
    for(k = 1; k <= j; k= k+1)
     \\ A code line of Θ(1)

θ( norte * m*(m+1)/2 )
θ( n*m + n*log ² (m) )
θ( metro ³ )
θ( norte ² )
θ( n ² *log ² (n) )

Respuesta: 4

Explicación: Para calcular la complejidad temporal de un programa basado en las entradas n y m, T(n, m), el primer paso es obtener el tiempo de ejecución de cada línea, ti ₍ n, m), como se indica a continuación:

// Se ejecuta n veces
$t_{1}(n, m) \in \Theta(n)$
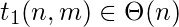
// itera log ₂ (m) veces, y está dentro de otro bucle que lo multiplica n veces
$t_{2}(n, m) \in \Theta ( n * log(m) )$
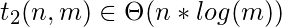
// Se ejecuta 2 + 4 + 8 + … + 2 ^log(m) veces
$2 + 4 + 8 + \ldots + 2^{log(m)} = 2* (2^{log(m)} - 1) = 2*m - 2$

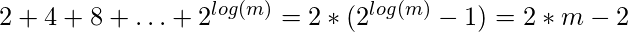
Esto también está dentro de un ciclo externo, el primer ciclo «for», que a su vez itera n veces

$t_{3}(n, m) \in \Theta ( m * n )$
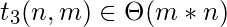
Lo mismo que la línea anterior, Θ( m*n )
$t_{4}(n, m) \in \Theta ( m * n )$

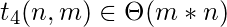
El orden total de tiempo de ejecución de este programa es:

$T(n, m) \in \sum_{i=1}^{4} \Theta ( t_{i}(n, m) ) \Rightarrow$

$T(n, m) \in \Theta(n) + \Theta(n* log(m)) + \Theta(n*m) + \Theta(n*m) = \Theta(n*m)$

Incluso se puede simplificar más de acuerdo con el conocimiento previo dado que dice que m ∈ Θ(n), o n ∈ Θ(m):

$T(n, m) \in \Theta(n^{2}) or \Theta(m^{2})$

Pregunta 5: Existe un vector de números enteros, llamado V[], que es de longitud “N”.
Para un problema específico (programa), se da que Σ _i=1^N |V[i]| = P.
¿Cuál es la complejidad temporal del siguiente fragmento de código? [No hace falta decir que P también es un número entero]

Tmp = -1;
  For r= 1 to N
   For S = 1 to V[r]
    Tmp = Tmp + 20;

O(N + 2*N*P)
EN P )
O( N ² )
O( PAG ² )
O( 2*P + N )

Respuesta: 5
Explicación: A continuación se indica el número de veces que se ejecutará cada línea y su complejidad temporal total:

// θ(1)
// N veces; entonces es de θ(N)
// No puede ser mayor que |V[r]| veces; entonces el número total de veces es O(Σ _r=1^N |V[r]| ) = O(P)
// Lo mismo que la línea anterior, O( P )

Para encontrar la complejidad de tiempo del programa dado, hay tres hechos a tener en cuenta:

Cada V[r] puede tomar cualquier valor entero (incluso cero o negativos), pero no importa, ya que todos los valores negativos conducirán a la no ejecución del segundo ciclo en lenguajes de programación como C. Sin embargo, en lenguajes de programación, se le permite contar hacia atrás (o iterar sobre) números negativos, pero los algoritmos no se analizan depende de los lenguajes de programación, y el análisis solo se basa en el algoritmo en sí. Qué decir con seguridad es la información que se da en la pregunta; por lo que una acción astuta es considerar el valor absoluto de |V[r]| y también usar notación para deshacerse de estar atascado. De lo contrario, se debe decir que el programa se ejecuta al menos tanto como el tiempo necesario para la ejecución del primer ciclo, o Ω(N)
Aunque el orden del tiempo de ejecución de este programa no parece depender de dos variables, no hay más información para un análisis adicional que se necesita para comparar P y N; por lo que la complejidad asintótica depende de los valores tanto de P como de N; en otras palabras, hay una función de complejidad T(N, P) en lugar de T(N).
La notación O() define un límite más flexible que el límite estrecho especificado por la notación &theta(); Por tanto, la suma de θ() y O() sería de tipo O(). En este problema, la complejidad temporal total del programa, que es la suma de todas las complejidades de las líneas de código, pertenece al conjunto O( 2 * P + N + 1 ) u O(2*P + N).

Teniendo en cuenta todos los factores mencionados anteriormente, una complejidad asintótica puede ser de Sin embargo, los coeficientes de las variables no son importantes en el paso final del análisis asintótico, ya que todas pertenecen al mismo conjunto de funciones de complejidad, y la complejidad también se puede expresar como O (|P| + N).

Fuente:

Una compilación de exámenes universitarios de Irán (con un poco de resumen, modificación y también traducción)

Publicación traducida automáticamente

Artículo escrito por j*g*1991 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta